CAEコラム
制御に関する運動と振動のモデル化 第1回 「連続体の振動のモデリング」
東京大学生産技術研究所 准教授 中野 公彦 先生
サイバネットは、エンジニアのための理論教育講座「CAEユニバーシティ」を主催しています。このコーナーではその「特別講座」として、講師の方などに専門分野をわかりやすくご紹介いただきます。
目次
はじめに
連続体とは、質量、ばね、減衰要素が明確に分離できる集中系と異なり、これらの要素が連続的に分布していると考えられた系を指します。従来は剛体(変形しない物体)と考えて問題のなかったものが、軽量化などに伴い、たわみやねじれが生じやすくなり、それらが系の挙動に与える影響を無視できなくなってきました。制御系モデリングにおいても、連続体を扱う必要があります。円柱のねじり振動を例に、連続体の力学を制御系設計と親和性の高い、線形な常微分方程式によって記述する手法の1つを紹介します。
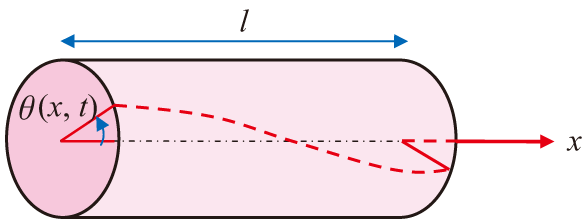
図1
ねじり振動の解析解
連続体の振動問題として代表的なねじり振動を例に、モデリングを行ってみます。図1に示すような、長さlである円柱(両端固定)に、ねじり振動が生じている系を考えます。
時間をt、円柱の左端を原点として軸方向の座標をx、ねじり角をとします。この時、支配方程式は以下のような、(古典的)波動方程式になります。
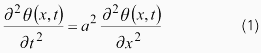
円柱の横弾性係数をG、極断面二次モーメントをJ、単位長さあたりの極慣性モーメントをI0とすると、aは以下のように定義されます。

波動方程式を解くために、変数分離形の解を仮定します。すなわち、ねじり角を以下のような時間関数q(t)と空間関数W(x)で表します。
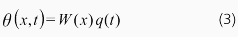
さて、系が角振動数piで振動していると仮定すると、q(t)は以下のように書くことができます。なお、φは位相を表します。
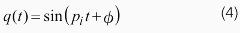
これを波動方程式に代入すると、以下の関係式が得られます。
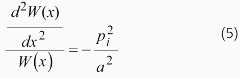
よって、W(x)の一般解は以下のようになります。なお、C1とC2は積分定数です。
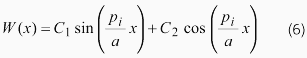
両端固定と考えると、以下の条件が成立します。
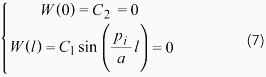
二番目の式が成立する条件は、以下の通りとなります。ただし、iは自然数となります。

これが固有角振動数であり、それは無数にあることがわかります。自然数iに対応する固有角振動数をi次モードの固有角振動数と呼びます。この固有角振動数に対応するW(x)をWi(x)とすると、Wi(x)は以下のようになります。これは、各地点xでの振動の振幅を表しており、i次のモード関数と呼ばれます。
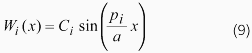
ねじれ角は、これら、全てのモードの時間関数と空間関数の和で表されます。すなわち、以下のようになります。
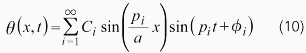
ねじり振動のモデリング
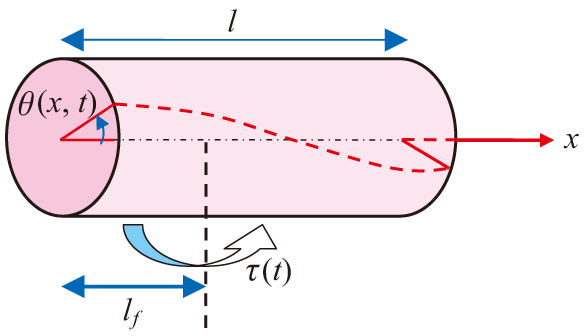
図2
図2のように、地点x=lfでモーメントτ(t)が強制入力として系に加えられると考えます。このモーメントに対する地点x=lθでのねじれ角の応答を求めることを考えます。強制入力がある場合の円柱の振動方程式は以下のようになります。
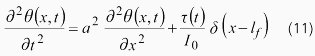
ここで、δ(x)はデルタ関数で以下の性質があります。
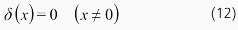
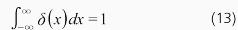
さて、両端固定の場合、強制入力によってモード形状の変化がないと仮定し、積分定数Ciを含む形でi次モードの時間関数qi(t)を定義しなおすと、ねじり角は以下の形式で表すことができます。
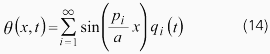
これを式(11)に代入すると以下の式が導かれます。
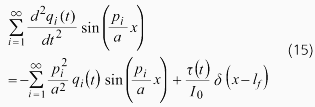
さて、モデリングに際しては、無数のモード全てを考慮することには無理があります。1つのモード(i=n)のみを考えることにします。
この1つのモードを抽出するために、モードの直交性を利用します。あるモード(n次とする)関数に異なるモード(m次とする)の関数を乗じて、モード関数の全範囲であるx=0からlまで積分を行うと、以下の通り0となります。
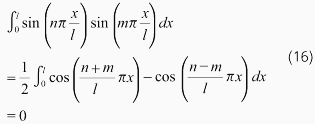
一方、同じモード関数を乗じて積分を行った場合は、以下の通り0とはなりません。
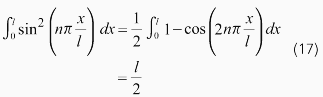
式(15)の両辺にn次モードのモード関数
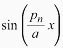
を乗じ、x=0からlまで積分を行うと以下の式が得られます。
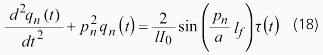
また、地点x=lθでのねじれ角は以下のようになります。
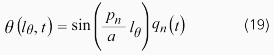
これより、ラプラス演算子をsとすると、強制入力から地点x=lθでのねじれ角までの伝達関数T(s)は式(20)のように求められます。強制入力があった箇所が節の場合、系への入力は全くなく、振動が発生しないことがわかります。また、観測位置(x=lθ)が節である場合は、系は振動していますが、それを観測できないことがわかります。この伝達関数は、状態方程式形式でも表現できます。
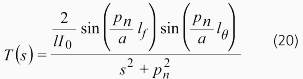
今回は、モード関数が正弦波になる時を例に説明しました。境界条件等によって形状は変わってきますが、モード関数には直交性がありますので、他の場合でも同様の手法が適用可能です。このように、連続体は1つもしくは限られた数のモードに着目すればモデリングは可能です。実際のシステムにおいても、限られたモードの動的挙動が支配的であることが多いため、今回の手法は有効と言えます。しかし、無視したモードの挙動が後になって制御系に影響を与えるケースもありますので、制御系設計を行う場合は、無視したモードが系に悪影響を与えないかどうか、十分に考えておく必要があります。





