CAEコラム
制御に関する運動と振動のモデル化 第2回 「アクティブサスペンション制御系設計のためのモデリング」
筆者:東京大学生産技術研究所 准教授 中野 公彦 先生
サイバネットは、エンジニアのための理論教育講座「CAEユニバーシティ」を主催しています。このコーナーではその「特別講座」として、講師の方などに専門分野をわかりやすくご紹介いただきます。
目次
はじめに
前回は、円柱を例に、連続体の振動のモデリング手法の一例を紹介しました。今回は、自動車や鉄道車両で乗り心地の向上を目的に設置されているアクティブサスペンションについて解説し、大型車のアクティブサスペンションのモデリング例を紹介します。
アクティブサスペンションとは
アクティブサスペンションとは、車体等に加速度計などのセンサを設置し、その信号に基づいて、サスペンションに取り付けられているアクチュエータが力を出すことにより、車体の姿勢変化を抑え、乗り心地や運転性能を向上させるものです。ばねや減衰器(ダンパ)などのパッシブ(受動)な要素に対して、アクチュエータというアクティブ(能動)な要素を用いるため、アクティブサスペンションと呼ばれています。油圧アクチュエータを用いたものが1980年代に乗用車にて実用化されています。また、鉄道においても、空気圧アクチュエータを用いたシステムが、新幹線用車両に設置されています。このようなアクティブサスペンションを、大型車で実現するためのモデリングを考えてみます。
サスペンションのモデル
アクティブサスペンションの制御系を設計する際には、図1に示すような1/4車両モデルと呼ばれるものが良く利用されます。車両の上下振動のみに着目したモデルであり、4つあるサスペンションを1つづつ切り出したような形になるため、このように呼ばれています。
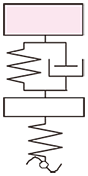
図1
2自由度系となり、比較的扱いやすいモデルです。また、図2に示すような1/2車体モデルと呼ばれるものもよく使われます。これは、進行方向に平行な線で車体を半分にしたようなモデルであり、乗り心地に大きな影響を与えるピッチングを考えることができます。タイヤは上下の動きのみを考慮するので、4自由度系となります。一般的な自動車の場合、前の方が重いので、重心位置はやや前方になります。
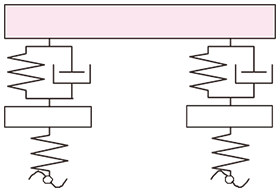
図2
図3に示すような1車両モデルも存在します。ピッチングに加え、ロールも考慮することができるようになります。
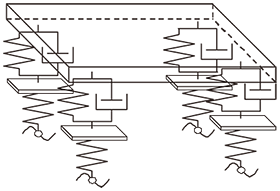
図3
フレームのねじれを考慮した大型車のモデリング
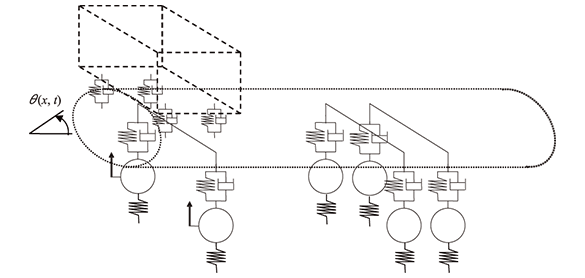
大型車は、乗用車と異なり、車体(フレーム)の上に、4つのキャブサスペンションを介してキャビンが置かれている構造になります。また、後輪も2軸あることが多いため、図4に示すように1車両モデルでは、3自由度(上下、ロール、ピッチ)のキャビン、3自由度(上下、ロール、ピッチ)のフレーム、1自由度(上下)のタイヤ6つとなり、12自由度系となります。なお、ロール剛性を向上させるスタビライザが入ることも多いのですが、ここでは省略しています。
今まで紹介したモデルは、車体が質点もしくは剛体であることを前提に考えています。しかし、大型車のように全長が長い車両は、ねじれのような弾性変形が生じやすく、それが車両の運動性能を悪化させることが考えられます。ねじれを抑えることができるアクティブサスペンションを実現するための、大型車のモ.デリング手法の一例(1)を紹介します。
大型車のフレームをねじれやすい円柱と考えます。前回説明しました通り、その場合のねじれ方程式は以下のようになります。
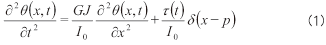
ただし、時間をt、円柱の左端を原点として軸方向の座標をx、ねじり角θ(x,t)を、円柱の横弾性係数をG、極断面二次モーメントをJ、単位長さ当たりの極慣性モーメントをI0、外部からのねじりモーメント入力をτ、その入力位置をp、δ(t)をデルタ関数とします。
計10か所のサスペンションからの反力のモーメントが外部ねじりとしてフレームに入力されることになります。各サスペンションからの入力をfi、各サスペンションの位置をpi 、中心軸と各サスペンションの距離をli とすると(ただし、i はサスペンションの番号とする)、ねじり方程式は以下のようになります。
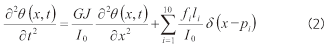
さて、フレームは両端自由なので、モード形状は余弦波状になります。サスペンションの力によってモード形状は変化しないと仮定し、車両の運動性能に影響を与えるのは1次モードであると考えれば、時間関数q(t)を用いて、ねじり角を以下の式によって表わすことができます。なお、Cは定数です。
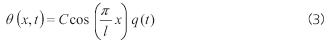
これを、式(2)に代入したねじり方程式の両辺に、1次のモード関数を乗じ、x=0からlまで積分を行うと以下の式が得られます。
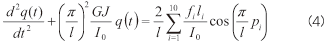
また、fi は、進行方向右側後輪2軸を考えると、サスペンションのストロークz2iとアクチュエータ出力uiを用いて、以下のように表わされます。なお、項の前の符号はサスペンションの位置によって変わります。

また、タイヤの質量をmi、タイヤの変形量をz0i、路面凹凸をz0iとすると、その運動方程式は以下のようになります。ここで、相対変位を用いているので、外乱(路面凹凸)は加速度項として表れます。
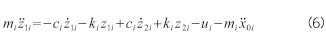
このようにして、全てのサスペンションに対して同様の方程式を記述し、フレームの剛体モードの運動方程式(上下、ロール、ピッチ)を組み合わせれば、ねじれを考慮した車両の方程式が導かれます。
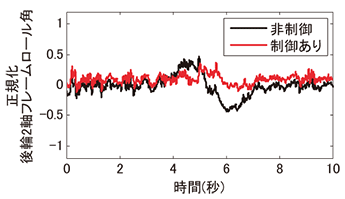
1つのモードに着目すれば、状態方程式を導くことができます。これにより、最適制御などの現代制御理論に基づいて制御器を設計することができるようになります。後輪の2軸にアクティブサスペンションを搭載した大型車がレーンチェンジをする時の後輪2軸目のフレームロール角(左右のサスペンションのストローク差をトレッドで除したもの)を図5に示します。制御の効果が表れていることがわかります。
最後に
ねじれとサスペンションのダイナミクスを組み合わせた大型車のモデリング例を紹介しました。なお、ねじれを表現する際には、車体を適当な場所で、前部と後部に分け、それらをねじりばねで接続するような集中質量系でモデリングを行うこともあります。各パラメータの値を実験値で合わせこめば、この手法でも十分に役立ちます。しかし、今回のような大型車の場合は、後輪に2つの軸があるため、集中質量系では、車体を切断する位置によって、ダイナミクスが大きく変化してしまう可能性がありました。そのため、モード形状を考慮することにより、1つのフレームを2つに切断しなくても良いモデリングを行いました。モデリングは、制御対象となる系の特性や制御を行う目的などに応じて、最良と思われるものを選択していく必要があります。




