みんなの公差
#15 正規分布と正規分布の確率
今回は、「正規分布」と「正規分布の確率」について解説します。
突然ですが、例題です。
例題:多数の板があり、それらの板厚が母平均μ=10、標準偏差σ=0.1で正規分布しています。
このとき、板厚が10.1以上となる確率はいくつでしょうか?
このような問いを前にして、ドキッとする方も少なくないかもしれません。私自身、答えが分かっていても一瞬戸惑うことがあります。高校時代、確率は勉強したけれど統計までは手が回らなかった、という方も多いのではないでしょうか。実際、受験科目にあまり出ないこともあり、正規分布やその応用についてしっかり学ぶ前に大学へ進学してしまったというケースは珍しくありません。大学では正規分布を学ぶものの、他の分布が次々登場して、結局どれも中途半端な理解のまま終わってしまう——そうして社会に出ると、ふとした瞬間にこのような問いを投げかけられて戸惑う、ということもあるでしょう。
もしこの問題を見て「すぐに分かる!」という方であれば、このコンテンツは必要ないかもしれません。
しかし、少しでも「自信がない」と感じた方には、ぜひ最後までご覧いただきたいと思います。
正規分布とは
式の意味を直感的にとらえることが大切です。
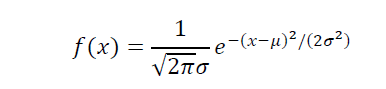
正規分布の曲線
たとえば人の身長、機械部品の軸の直径、穴のサイズなどがこういった分布の代表例です。
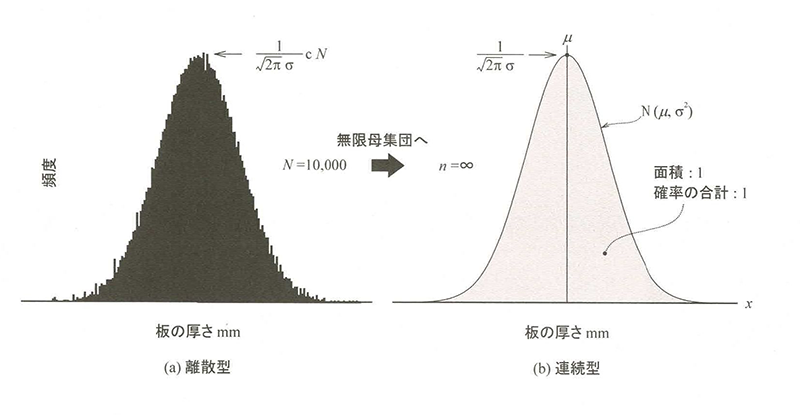
個別部品のヒストグラム
個別の部品を測定して並べるとわずかなギザギザがありますが、右側の図のように無限大のデータを集めて並べると、このように理想的なカーブを描けます。
この分布を数式で表したものが、先ほどの複雑そうに見える式です。
正規分布表
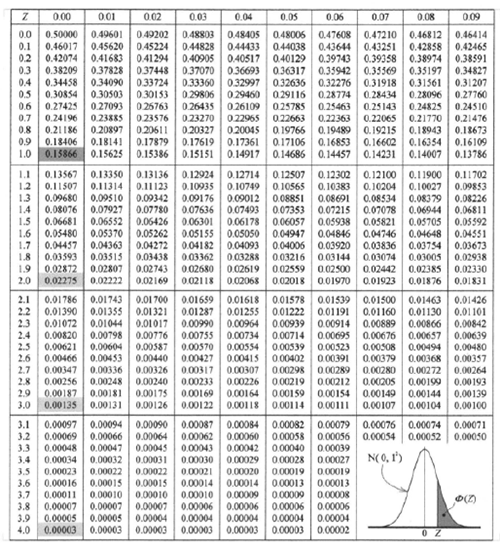
正規分布表のサンプル
実際の計算では、数式そのものではなく「正規分布表(Z表)」を用います。
正規分布表を使うためには、まず「標準化(または基準化)」という処理が必要です。
正規分布表を見ると拒否反応を示す方がいるかもしれませんが、ぜひ動画を見ながら Excel にてご自身で作っていただき慣れていただければと思います。
それでは先ほどの例題に戻ります。
例題
多数の板があり、それらの板厚が母平均μ=10、標準偏差σ=0.1で正規分布しています。
このとき、板厚が10.1以上となる確率はいくつでしょうか?
標準化(基準化)
正規分布表を使う際に行う下準備があります。それが、標準化 (基準化) と呼ばれるものです。
標準化とは、平均を0、標準偏差を1とした正規分布に変換する操作です。
たとえば、平均10mm、標準偏差0.1の板厚分布があった場合、それをZスコア(Z値)として「Z = (X - μ) / σ」で表します。

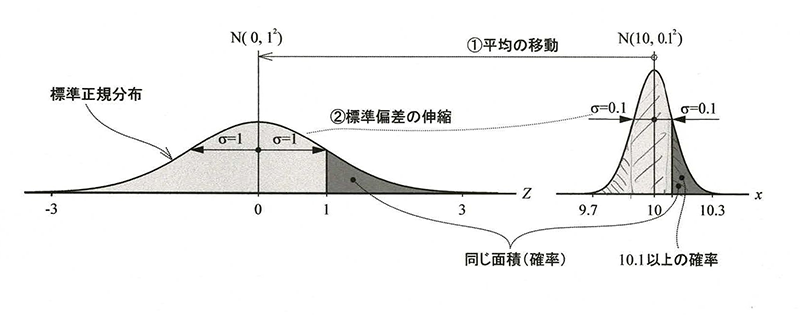
この標準化を行う理由は「正規分布表を使うため」なのです。
正規分布表の使い方
正規分布表は、横軸が小数第二位(0.00〜0.09)、縦軸が小数第一位(0.0〜4.0)で構成されており、Z値に対応する確率が一覧化されています。
例題ではZ = 1.0でしたので、正規分布表から読み取れる値は 0.15866、すなわち 15.866% です。
これは、Zが1.0以上である確率を意味します。つまり、元の板厚が10.1mm以上となる確率も15.866%ということになります。
Excelを用いた正規分布の計算
関数 =1-NORM.DIST(10.1, 10, 0.1, TRUE) を用いることで、先ほどと同じ15.866%という結果が得られます。

正規分布表をExcelで作ってみよう!
あらかじめフォーマットを配布いたしますのでダウンロードして動画を見ながら実践的な演習が可能です。
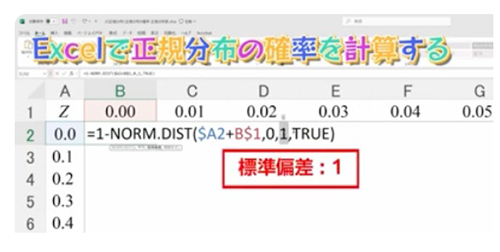
ここでも「1-NORM.DIST」の数式を用います。配布用Excelのテキストボックスに数式が入っていますのでそれをコピー&ペーストしてください。
左のセルと上のセルを足して、平均 (=0)、標準偏差 (=1) をかけると正規分布の確率が出ます。テンプレートに関数を埋め込み、セル参照を固定するために「$」を用いることを忘れずに。コピー&ペーストするだけで、簡単に正規分布表が完成します。また、特によく使うZ値(1.0、2.0、3.0など)はセルに色をつけておくと便利です。
正規分布の求め方
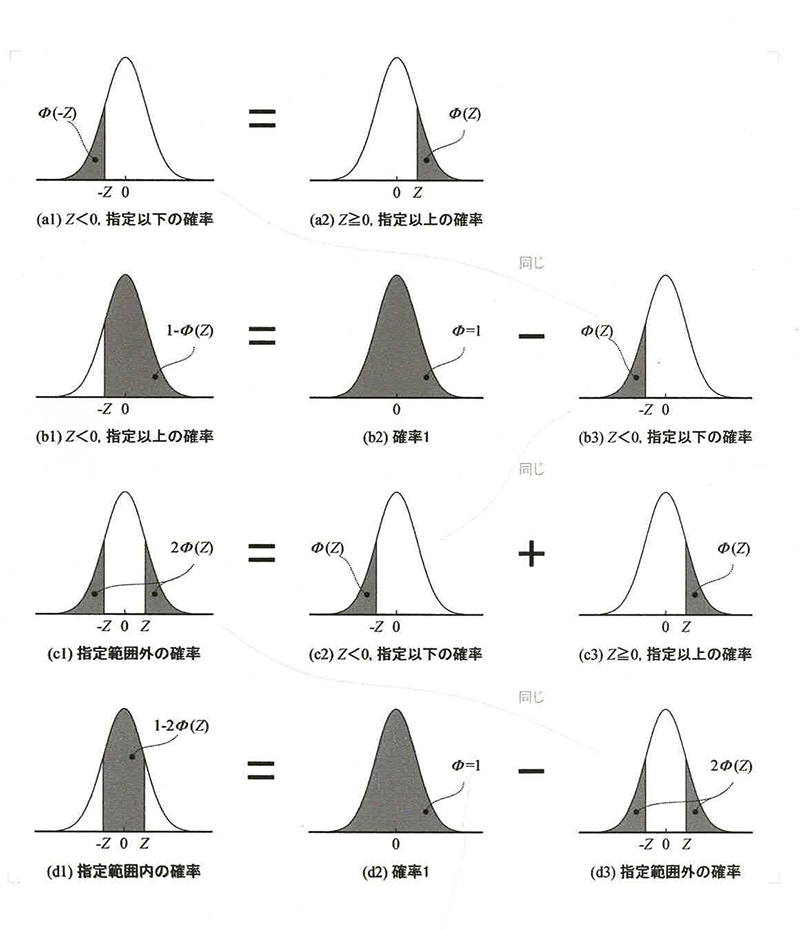
正規分布の確率の求め方にはバリエーションがあります。
さまざまなケースに応じた確率の求め方を知っておくと便利です。動画にて下記の求め方をご紹介しています。
図や表を使えば直感的に理解できる内容も、実際に問題として出されると戸惑うものです。
しかし、一度体系的に理解しておけば、どんな問題にも対応できるようになります。
まとめ
今回ご紹介した方法を通じて、複雑に見える数式も、Excelを活用すれば身近で扱いやすいものになります。
以降の動画は、この正規分布を基盤とした確率の応用方法や、他の分布についてもご紹介していきます。
まずは正規分布をしっかりマスターしておきましょう!
「正規分布と正規分布の確立」を動画で解説!
より詳細な内容は、YouTube チャンネル「みんなの公差」で解説しています。ぜひご視聴ください。