#11 公差累積の感度

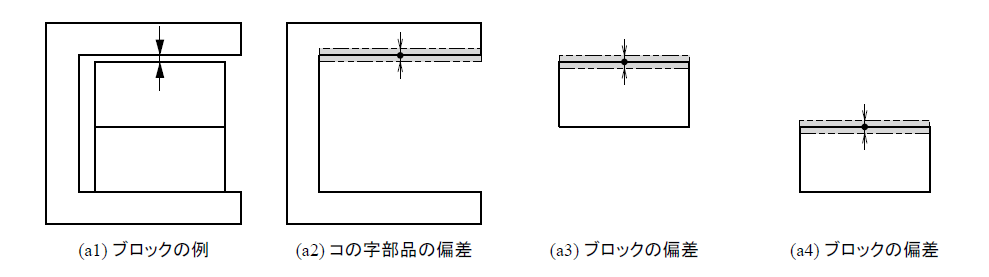
これまでの例では、ブロックの例(a1)のように一直線上で2つの板とコの字型の部品が関係しており、それぞれの解析寸法への影響は、コの字型の部品(a2)、上側のブロック(a3)、下側のブロック(a4)も同様に影響を受けるというものでした。具体的には、ある部分が1動いた場合、解析寸法への影響も1倍となっていました。しかし、公差解析を進めると、必ずしも影響が1倍とは限らない場合があることがわかります。

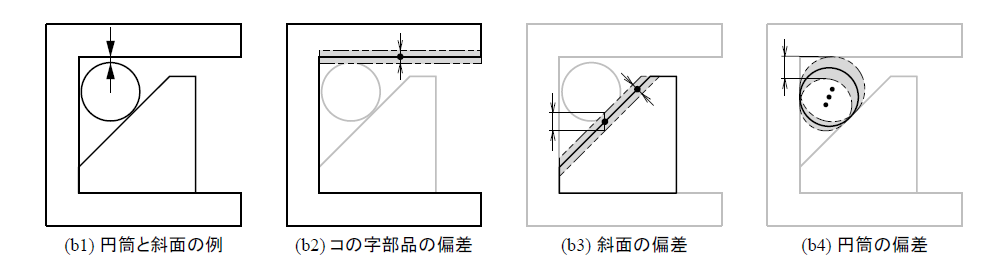
例えば、上側の2つのブロックを斜めにし、片側を円筒状にした場合(b1)を考えます。
この構造は特定の機能を持つ部品ではありませんが、できるだけシンプルな例として取り上げます。
この状態で、解析寸法として考えるポイントを見てみると、コの字型の部品の影響はこれまでと変わらず、1動いた場合は解析寸法への影響も1倍となります。

しかし、斜面の場合は異なります。
斜面が1動くと、動きが斜め方向になるため、解析寸法への影響は実際には √2 倍になります。
このように、解析寸法への影響の倍率が変化するときには注意が必要です。
また、ここでは詳細な解析は省略しますが、円筒部分も大きな感度を持っています。
円筒の直径が大きくなったり小さくなったりすると、その変化は単なる直径の変化にとどまらず、左下方向へすぼまるよう感じになりますので、その結果、解析寸法への影響は予想以上に大きくなります。
このように、解析寸法が1動いたときに影響が必ずしも1倍とは限らない場合があり、その点を十分に考慮する必要があります。

公差解析では、さまざまな構造物が考えられます。
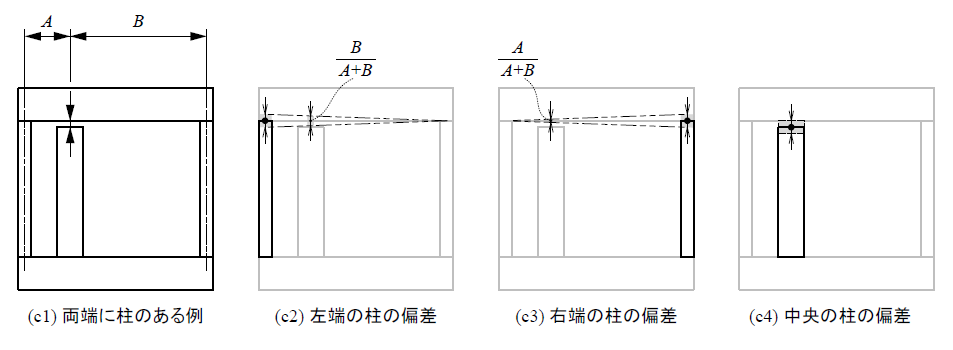
例えば、天井と床があり、左右を柱で支えられている構造(c1)を考えた場合、解析寸法として考えるポイントが中央にあるとします。
このとき、Aの部分が1動いた場合に、解析寸法も1動くかというと、必ずしもそうではありません。影響の大きさはAとBの比率によって決まります。

例えば、Aが1動いたときの影響の大きさは，三角形の相似を利用して求められます。
計算すると、解析寸法の動きは(A+B)/Bで表されます。Aが小さいほど感度が大きく、Aが大きいほど影響が小さくなります。
同様に、右側の柱が動いた場合も、解析寸法への影響は(A+B)/Aで表されます。
一方、解析寸法のある柱自体が1動いた場合は、解析寸法も1動くため、特に考慮する必要はありません。

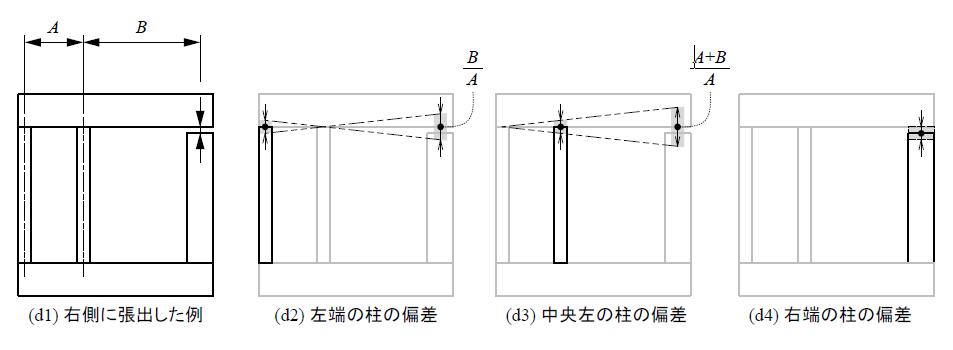
(d1) の例は(c1)と似ていますが、解析寸法の柱が右端に寄り、支えている柱は左隅に2本あります。
メカ設計をされている方ならわかると思いますが、この2つの寸法がばらつくと、解析寸法へ大きく影響を与えます。例えば、ペンの端をもって少し動かすと、先端が大きく動くのと同じ原理です。両端を持っていれば真ん中の動きは小さくなりますが、片側だけ持って動かすと、反対側の端は大きく動きます。

この場合の感度計算も三角形の相似を使って求められます。
左隅の柱(d2)が動いたとき、影響はB/Aで決まります。Aが小さいと感度が大きくなります。
中央左の柱(d3)が動いた場合、感度は(A+B)/Aで求められます。
解析寸法のある右側の柱(d4)自体が1動いた場合は、解析寸法も1動くため、特に考慮する必要はありません。

張り出した構造物や斜面によって感度が大きくなる場合があるため、機械の構造設計を考える際には、感度が小さくなるような設計をすることが重要です。

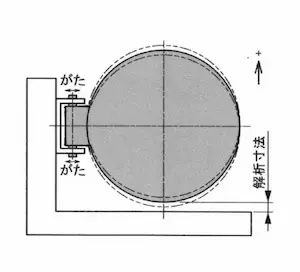
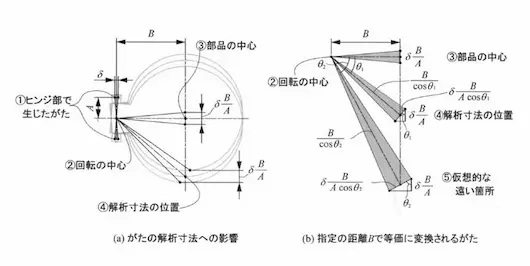
感度が問題になる例として、自動車の給油口のような丸い扉を考えます。
この扉が開閉する際に、隙間が適切である必要があります。
扉が2か所のヒンジで支えられている場合、ヒンジの距離の半分をA、ヒンジの中心から扉の中心までの距離をBとすると、ヒンジのずれがΔだった場合、その影響はδ(B/A)で表されます。

また、扉が，がたによって回転すると、隙間が変化します。
すきまの解析をする場所が，遠くに行けば行くほど影響が大きくなりますが、縦方向の成分のみを考えると、結局δ(B/A)となります。
このように、回転による影響も考慮しながら設計することが重要です。

感度解析を行うことで、設計時に予測される影響を正確に把握し、より精密な構造を作ることが可能になります。