#10 公差累積のループ
公差累積のループとは
これまでの動画で公差解析の対象としていたのは、「板の積み上げ」といった非常にシンプルな構造でした。
今回はそこから一歩進んで、より複雑な構造物を取り扱う際の「公差累積のループ」について説明します。
ここでは、板の積み上げよりもやや複雑なサンプルを用いて公差累積図の説明を行い、その中で「公差累積のループ」について解説します。
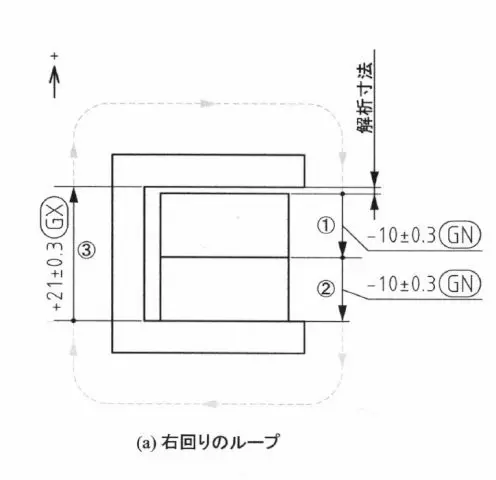
この例では、板が2枚とコの字型の部品があります。
従来、板の厚さのサイズや公差を二乗して足してルートをとるといった手法を用いてきましたが、この例では単純な積み上げだけではなく、より考慮すべき点が増えます。
この例では、コの字型の部品の上側にわずかな隙間が存在します。
ここがとても重要で、部品同士が干渉してはいけませんし、隙間が大木すぎてもいけません。
この隙間を「解析寸法」と名前をつけておきます。
公差解析図（公差累積図）とは
解析寸法の公差解析を行う方法は、基本的には構成する部品の接触関係を順に追っていくというシンプルなものです。
具体的には、上側の部品①から開始し、次に接触している部品②の該当する寸法を加え、さらに接触しているコの字型部品の③の部品をいれます。
そうすると1周ぐるりと回ってきます。
図にうっすらと書いてある矢印の線をたどると、ぐるっと一回りループのような形なっています。
解析寸法をめぐる一回りのループを作成することが、公差解析の第一歩となります。
このような図を「公差解析図」とか「公差累積図」と呼んでいます。
公差解析図（または公差累積図）を作成する際には、一般的に上方向をプラス、右方向をプラスとすることが多いですが、統一性があれば他の基準でも問題ありません。
この例は非常に簡単で、①と②は矢印が下に向いているのでマイナス、③のように矢印が上向きだったらプラスという風に符号を付けていくと、解析寸法を得るのが非常に楽になります。
①と②に、-10±0.3が２つあって、③は+21±0.3です。
これを計算すると、ワーストケースで1+-0.9という解析の結果になります。
解析寸法を求める際には最短ルートを取ることが重要
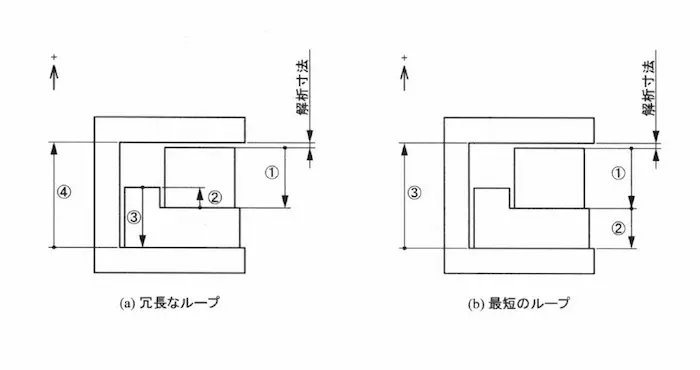
(a)の図は(b)と比較をすると、(a)の図は下に下がって上に上がり、また下に下がるといった無駄が発生しています。
解析寸法を求める際には、最短ルートを取ることが重要です。
誤ったルートでは、必要以上に寸法を追加してしまう場合があり、公差の累積が大きくなります。
特に、より複雑な構造物では、このようなミスが発生しやすいため、注意が必要です。
「公差累積のループ」を動画で解説！
より詳細な内容は、YouTube チャンネル「みんなの公差」で解説しています。ぜひご視聴ください。
#10 公差累積のループ
本動画に関するご質問や、鈴木先生に解説して欲しい内容に関するリクエストなどございましたらお気軽にお問い合わせください。