みんなの公差
#07 二乗和平方根
なぜ二乗した和のルートをとる?
二乗和平方根とは?

例:板を4枚積み上げる
「40という寸法に対して、ルートの中に0.3の2乗を4回足したもの」
これを二乗和平方根と呼んでいます。

二乗和平方根をシグマを使って書くとこのようになります。
形はワーストケースの式に似ていますが、感度と公差半値をかけたものを2乗して足していきます。
感度は、この場合「1」で考えなくてもいいです。「n」に関しても同じです。
ここまでは、インターネットを検索するとよく出てくる計算です。
"全部を足す"か、"二乗して足してルートを取る"か、この2つが、公差解析の基礎中の基礎だからです。
形はワーストケースの式に似ていますが、感度と公差半値をかけたものを2乗して足していきます。
感度は、この場合「1」で考えなくてもいいです。「n」に関しても同じです。
ここまでは、インターネットを検索するとよく出てくる計算です。
"全部を足す"か、"二乗して足してルートを取る"か、この2つが、公差解析の基礎中の基礎だからです。
なぜ二乗した和のルートをとる?
二乗和平方根の由来
二乗和平方根の由来の話をしていきたいと思います。
なぜ二乗してルートをとるのでしょうか?
なぜ二乗してルートをとるのでしょうか?
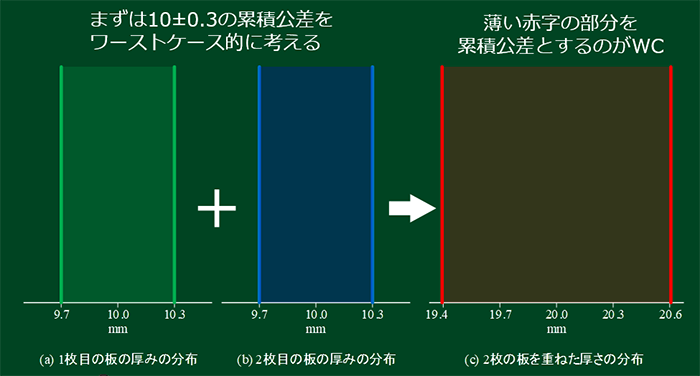
一番右(緑)と中央(青)の2つは、"10±0.3" この範囲の中に板の厚さが必ずなければならないという図です。
今回は 4 枚ではなく、2 枚の板の積み重ねです。
2 枚の板を積み重ねた時のワーストケース(右側の赤)は、20±0.6 になります。
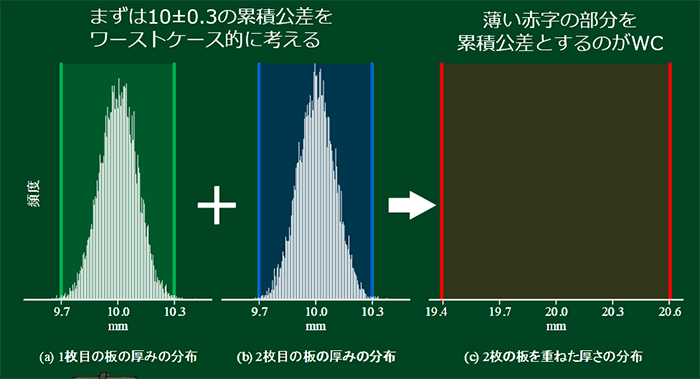
今回は公差の中で「正規分布した場合」を考えています。
どちらの板もこの 9.7 から 10.3 の範囲の中で正規分布をしていると考えてください。
厳密には、少しはみ出ていますが、ほぼ全ての99.7%が入っていると考えてください。
この中からランダムに、それぞれ1個選びます。
例えば、「1枚目から9.9、2枚目から10.1を選んだ時に 20.0 になりました」という感じです。
これをたくさん行った時に、この分布がどのようになるでしょうか?
どちらの板もこの 9.7 から 10.3 の範囲の中で正規分布をしていると考えてください。
厳密には、少しはみ出ていますが、ほぼ全ての99.7%が入っていると考えてください。
この中からランダムに、それぞれ1個選びます。
例えば、「1枚目から9.9、2枚目から10.1を選んだ時に 20.0 になりました」という感じです。
これをたくさん行った時に、この分布がどのようになるでしょうか?
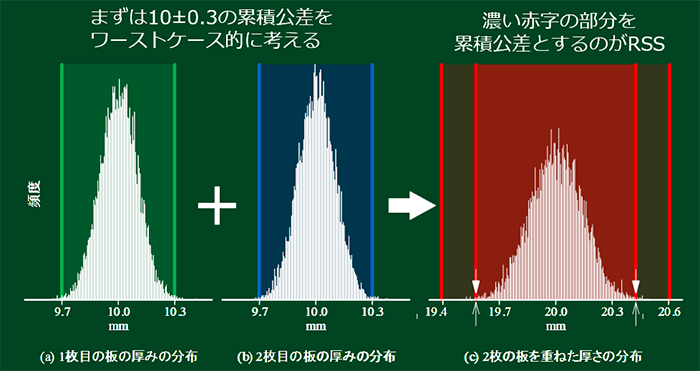
実際にモンテカルロシミュレーションで解析したものが上記の図です。
分布を見てみると、ワーストケースの範囲の中に目いっぱい入るのではなく、もう少し狭い範囲に収まっています。
「この範囲に収まるんだよ」というのが、実は二乗和平方根なのです。
このように「2 つの正規分布の中から無作意に選んで、さらにまた分布を作る」という、まさに「2つの板を抜き出して高さを測ってみる」ということを実施すると、ワーストケースの範囲よりも内側に分布し、外側に出ることはほとんどないのです。
この計算が 二乗和平方根の由来になっています。
もう少し細かく言うと「分散の加法性」と言われています。
分散・標準偏差など関しては、また「統計」の章を設けていますので、そこでさらに詳しく説明させていただきます。
このように公差の範囲の中で正規分布してる、それを合成したものが実はワーストケースほど広がってないということを利用しているのが二乗和平方根です。
二乗和平方根を用いる条件
二乗和平方根を使うには条件があります。
計算した結果が非常に設計者にとっては有利な条件ですので、これを無条件に使いたくなる気持ちを持ちますが、いくつか制限があります。
計算した結果が非常に設計者にとっては有利な条件ですので、これを無条件に使いたくなる気持ちを持ちますが、いくつか制限があります。
各部品の寸法が正規分布に従う
各部品の寸法が正規分布に従うというのが大前提です。
例えば正規分布ではなくもっと尖りが低い、もっと円のように丸い分布を持つ場合もあるかもしれません。
平らな分布を持つ場合もあるかもしれません。
その場合は、この前提が崩れてしまいますので、もう少し外にはみ出ることになります。
そういった時には二乗和平方根が成り立ちません。
例えば正規分布ではなくもっと尖りが低い、もっと円のように丸い分布を持つ場合もあるかもしれません。
平らな分布を持つ場合もあるかもしれません。
その場合は、この前提が崩れてしまいますので、もう少し外にはみ出ることになります。
そういった時には二乗和平方根が成り立ちません。
かたより度 k = 0
「かたより度」とは、分布が今この公差の範囲にぴったりと収まっていますが、”かたよる”というのは、分布が中心よりも右に行ったり左に行ったりすることを表しています。
もし”かたより”が生じた場合、幅だけではなくて位置も含めて、公差の範囲に分布が収まっていなければ、二乗和平方根が成り立ちません。
もし”かたより”が生じた場合、幅だけではなくて位置も含めて、公差の範囲に分布が収まっていなければ、二乗和平方根が成り立ちません。
各部品は、無作為抽出で組み立てられる
”9.8から1個板を取ってくる” ”10.1の板を取ってくる”というように、無作為抽出で選んだ結果に対し、厚さを調べてヒストグラムにしてみると、その作業の中で得られるのが二乗和平方根ですので、そうではない場合は成り立ちません。
どのような場合にそれが成り立たないのでしょうか。
例えば、金型を使ったプレス部品やモールド部品で物を作る場合、正規分布になってるかと言われると金型には摩耗があるので、ある時だけを取ればおそらく正規分布をしてると思いますが、だんだん中心は左右どちらか一方向にシフトしていくことが考えられます。
このようなことが起こる場合には、二乗和平方根が使えません。
もし作った順に投入するということであれば、それは無作意抽出ではなくなってしまうのではないでしょうか。
これは、実際の生産では難しいことだと思います。
全部の部品を1度に生産して、それをランダムに組み合わせるとわけではなく、作った端からあるロットで出荷してくことになるので、無作為抽出で組み立てられているかというと、そうではないと思います。
ただそれぞれの部品が全部同ロットで作られてるわけではなく、1000個で1個のロット、100個で1個のロットかもしないので、そういうものを全部組み合わせると、無作為抽出に近い状態かもしれません。
あくまでここでは統計的な計算ですので、無作意抽出を前提に計算されています。
どのような場合にそれが成り立たないのでしょうか。
例えば、金型を使ったプレス部品やモールド部品で物を作る場合、正規分布になってるかと言われると金型には摩耗があるので、ある時だけを取ればおそらく正規分布をしてると思いますが、だんだん中心は左右どちらか一方向にシフトしていくことが考えられます。
このようなことが起こる場合には、二乗和平方根が使えません。
もし作った順に投入するということであれば、それは無作意抽出ではなくなってしまうのではないでしょうか。
これは、実際の生産では難しいことだと思います。
全部の部品を1度に生産して、それをランダムに組み合わせるとわけではなく、作った端からあるロットで出荷してくことになるので、無作為抽出で組み立てられているかというと、そうではないと思います。
ただそれぞれの部品が全部同ロットで作られてるわけではなく、1000個で1個のロット、100個で1個のロットかもしないので、そういうものを全部組み合わせると、無作為抽出に近い状態かもしれません。
あくまでここでは統計的な計算ですので、無作意抽出を前提に計算されています。
各部品の寸法・がたなどは独立
”1枚目の板が厚くなった時に2枚目の板は別に厚くなるわけではない”というのが「独立の状態」です。
機械の設計では独立ではないケースというのは少ないのですが、そのような場合もまれあります。
機械の設計では独立ではないケースというのは少ないのですが、そのような場合もまれあります。
解析寸法は、各寸法の和または差 (積になる例…×)
板を積み重ねるのは、単純に和です。
差の場合もあります。例えば、「穴と軸の隙間がいくつになるか」は差になります。
稀に掛け算になる場合や分母に来る場合がありますが、この場合、二乗和平方根がそのまま使えるわけではありません。
差の場合もあります。例えば、「穴と軸の隙間がいくつになるか」は差になります。
稀に掛け算になる場合や分母に来る場合がありますが、この場合、二乗和平方根がそのまま使えるわけではありません。
Question : 設計と製造で、どちらの公差を優先すべきかは立場で異なるか
続きはみんなの公差にて動画で解説!
より詳細な内容は、YouTube チャンネル「みんなの公差」で解説しています。ぜひご視聴ください。
#07 二乗和平方根
本動画に関するご質問や、鈴木先生に解説して欲しい内容に関するリクエストなどございましたらお気軽にお問い合わせください。