みんなの公差
#06 ワーストケース
公差解析における基本中の基本「ワーストケース」を徹底解説
ワーストケースとは?
まずは基本をおさえましょう。
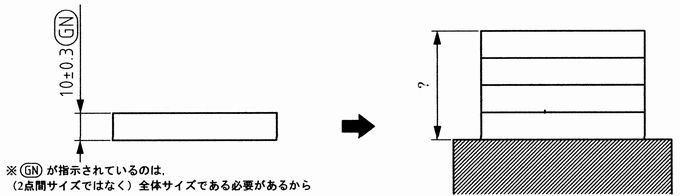
四角い板を 4 枚積み上げた場合のワーストケース
この例では、四角い板を 4 枚積み上げております。
10±0.3で指示された板の厚さがあります。それを4枚積み上げた時に、この高さが最大でいくつになるか、最小でいくつになるかということを考えてみます。
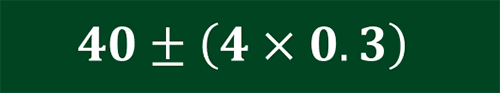
4枚積み上げた板の高さは、左の式のようになります。
「4」は、4枚分という意味で、「0.3」は、プラスの場合は、各板に+0.3、マイナスの場合は、各板に -0.3 であると考えて高さを見積もることができます。
これがワーストケースです。

ワーストケースを数学らしい式にすると左のようになります。
「 a 」は、”感度または係数” です。
例のように板を積み上げるだけであれば、「 1 」として考えますが、今後登場する複雑な公差解析においては、ここが1ではなく1.5や2に増える場合があります。今回は、「 1 」と考えてください。
「 ti 」は、今回は4枚の板なので、添え字の「 i 」が 1 から 4 まで変わります。
それぞれの公差の半分、ここでは板の厚さは±0.3なので、公差半値は「 0.3 」となります。
Question : 「 10±0.3 」とした時に、公差はいくつになりますか?
モデルワーストケースを用いる場合
生産性<安全性(ごくわずかな不良も許されない)
生産性よりも安全性の方がとても優先されていて、ごくわずかな不良も許されないという場合にワーストケースを使います。
安全性を重視すべき場合には、ワーストケースを使わざる得ない時もあるかもしれませんが、ワーストケースは、安全性を重視しすぎるところがあります。
累積要素数が少ない
累積要素数というのは、先ほどの例で言うと板の積み上げの板の枚数です。
「じゃんけん」を例に考えてみましょう。
「じゃんけん」は、3 分の 1 の確率でグチョキパーをだします。
例えば、私が 4 人と(1対1で連続して)じゃんけんをする場合、4人とも負ける確率はどのくらいでしょうか?
1人であれば負ける可能性は、2分の1でかなり高いです。
累積要素数が少ない2人などの場合、負ける可能性があると感じますが、これが 10 人 15 人となるとずっと負け続けるかと言われたら、どこかで勝つこともあるのではと感じませんか?
このように、ワーストケースをずっと使い続けるのはあまり生産的ではありません。
累積要素数が少ない(じゃんけんで例えると2人や3人)時にワーストケースを使うことはあっても、累積要素数が多い(じゃんけんで例えると10人や15人)時にワーストケースを使う必要はありません。
(公差の累積への)要素数が少ないときにワーストケースを使います。
複数の金型で1種類の部品を生産. 複数の分布が合成され、分布が予測できない
生産や製品の種類によっては、たくさんの金型で部品を作っている、またはたくさんのサプライヤさんによって成り立っているものがあります。
それぞれの生産の状況が分かりづらい、「分布」などが合わさって出てくるので、予想しづらいという場合にワーストケースを使ってもよいかもしれません。
組立時に受ける力、重力、ばねの力などによって、組み立てられる部品が両極端に寄る
・公差解析をする際に、その部品が重力で必ず右側に寄る、下側に寄る
・バネの力によって右側に寄る
このように、「必ずこうなる」ということが分かってる時にワーストケースとして考慮するということがあると思います。
今後、ワーストケースや他の公差解析の方法と比べることで特徴が分かってくると思います。
「ワーストケース」について、みんなの公差にて動画で解説!
より詳細な内容は、YouTube チャンネル「みんなの公差」で解説しています。ぜひご視聴ください。
#06 ワーストケース
本動画に関するご質問や、鈴木先生に解説して欲しい内容に関するリクエストなどございましたらお気軽にお問い合わせください。