みんなの公差
#03 公差の累積
「公差の累積」と関係する公差解析用語について解説
公差の累積について解説
10±0.3 のサイズの板を4枚積み上げたときの高さはいくつになるか
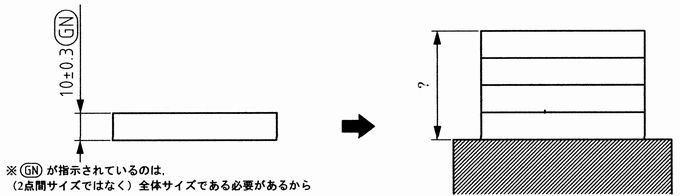
公差で指示がされている板を四枚積み上げるとします。
その時のこの板の高さは一体いくつからいくつになり得るか設計上予測したいというニーズがあります。
公差の累積について、これは一番シンプルな出発点になると思います。
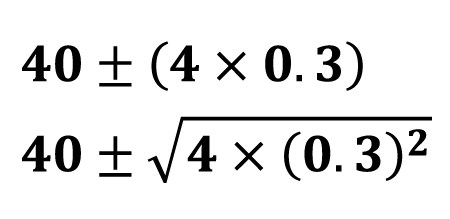
この高さを予測するには、この2つの計算方法だけでほぼ完結します。
基本的な公差解析は、入口が非常に簡単にできているのが特徴です。
そして、この2つの計算に限らず、公差に関わる計算一般のことを「公差計算」と呼びます。
公差の累積とは?
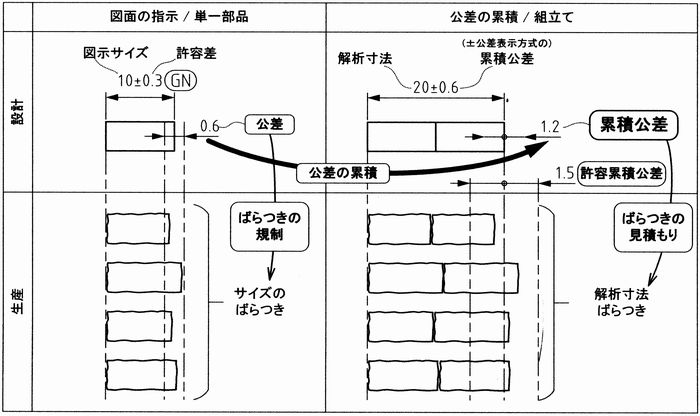
この図の左側では、単品部品で上記と同じく10±0.3という指示があります。
±0.3という指示がされているため、サイズは,設計の10よりも、最大で0.3最小で-0.3、この範囲が公差に相当します。
設計時にはこの範囲を指定しますが、生産時にはその範囲の中で、小さかったり大きかったりとばらつきが出ます。
言い方を逆にすると、このばらつきを規制するのが「公差」です。
次に、単一の部品ではなく、それを2つ重ねて組み立てるケースを考えてみましょう。
単純に足せばいい話ですので20±0.6が最大の範囲になります。
公差を足し合わせる際、二乗してルートを取るという方法で、この範囲に収まるという考え方を、「公差の累積」と呼んでいます。
±0.3という指示がされているため、サイズは,設計の10よりも、最大で0.3最小で-0.3、この範囲が公差に相当します。
設計時にはこの範囲を指定しますが、生産時にはその範囲の中で、小さかったり大きかったりとばらつきが出ます。
言い方を逆にすると、このばらつきを規制するのが「公差」です。
次に、単一の部品ではなく、それを2つ重ねて組み立てるケースを考えてみましょう。
単純に足せばいい話ですので20±0.6が最大の範囲になります。
公差を足し合わせる際、二乗してルートを取るという方法で、この範囲に収まるという考え方を、「公差の累積」と呼んでいます。
公差解析に関わる疑問
公差解析では幾何公差をどうすべき?がたをどう見積もるか?Cp、Cpkとの関係は?
実際に実務等で公差解析をしていくと、いろいろな疑問が湧いてきます。
- 公差解析では,幾何公差をどうすべき?
- 既存の公差計算では余裕が多すぎ/少なすぎ!適度な計算法はないか?
- がたをどう見積もるか?
- 公差解析とCp,Cpkとの関係?
- Cp,Cpkなどをどう図面へ反映する?
- データムの浮動は公差の累積に関係する?
こういった疑問に対して、今後の動画で回答していきたいと思います。

データムの浮動
穴がある部品があるとします。
穴を部品の基準として測定機に取り付けた際に、カタカタすることがあります。
このカタカタする場所を「浮動」と呼んでいます。
図面の基準になるデータムのカタカタとした動きを「浮動」と呼ぶことは、JISでも定められています。
※JIS B 0023 : 1996 4.3参照
部品と部品の組合せによってできる「がた」とは、公差解析用語で区別されています。
「公差の累積」に関する公差解析用語
JIS B 0625で規定された公差解析用語から、公差累積に関わる用語にについて説明いたします。
- サイズ差、幾何偏差、ばらつき
- 公差の累積(公差累積)
- 解析寸法
- 許容累積公差
- 累積公差
- 公差解析
図を使って「公差の累積」に関する用語を分かりやすく解説
より詳細な内容は、YouTube チャンネル「みんなの公差」で解説しています。ぜひご視聴ください。
#03 公差の累積
本動画に関するご質問や、鈴木先生に解説して欲しい内容に関するリクエストなどございましたらお気軽にお問い合わせください。