公差解析入門
分散と標準偏差の違いは?
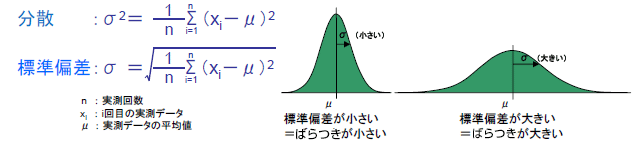
ではなぜ一般的にばらつきの大きさを示す際、分散ではなく標準偏差が用いられるのでしょうか。
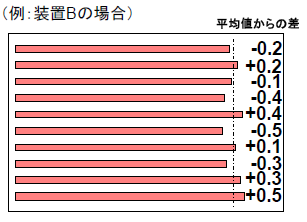
まずばらつき具合の評価ですが、例えば装置A、装置Bそれぞれで製造した部品の長さばらつきを下図に示します。
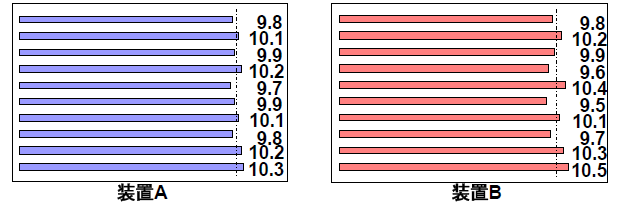
この場合、どちらの装置を使っても長さの平均は「10mm」になります。
次に、それぞれの装置で製造される部品について、全体での長さばらつき具合を数値化するため、
ばらつき=Σ(測定値−平均値)
を求めてみます。
しかしながら、この式ではプラス側のばらつきとマイナス側のばらつきが相殺してしまい、結局どちらの装置の結果も「0」となってしまいます。
そこで符号の影響を排除するために、
ばらつき=Σ(測定値−平均値)2
でばらつきを求めてみます。
この式で求めたばらつきは、装置Aが「0.38」、装置Bが「1.10」となり、装置Bの方がばらつきが大きいことが、数値として確認できます。
ただし、この算出方法では測定値の数が増えるほど値が大きくなるため、異なったサンプル数の結果同士を比較できません。
例えば装置Aのサンプルが30個だと
0.38+0.38+0.38=1.14(装置A) > 1.10(装置B)
となり、装置Aの方がばらつきが大きくなります。
そこで、
ばらつき=Σ(測定値−平均値)2 /データ数
とすることにより、異なったサンプル数の結果同士も比較することが可能となります。
この式で求めたばらつきを示す数値が、上記の式で表される「分散」です。
この様に、分散はその算出過程で符号の効果を排除するため2乗しています。
従って、分散は長さのばらつきであれば、長さの2乗(例:mm2 )の単位を持ちます。
しかしながら、通常長さのばらつきを評価する際には、同じ次元の長さで評価する方が感覚的に分かりやすいため、一般的にばらつきを表す場合は、分散の平方根である「標準偏差」が用いられます。