公差解析入門
分散の加法性
統計計算の中で利用されている分散の加法性とは?
分散の加法性は、統計学上の基本ルールで、以下のように表されます。
分散の加法性の基本ルール(統計学)
各変数が独立していること。
計算に利用する変数が他の変数に影響しないこと
![]()
各変数の合計は線形表現の式で表される。![]()
![]()
各変数の合計の分散の値は、各変数の分散の和に等しい。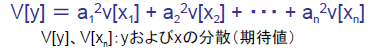
この考えを公差解析の世界に置き換えると次のようになります。
分散の加法性の基本ルール(公差解析)
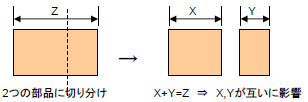
各変数が独立していること。
→ 各寸法が他の寸法に影響しないこと


各変数の合計は線形表現の式で表される。
→ 求める寸法が線形表現の式となること
![]()

各変数の合計の分散の値は、各変数の分散の和に等しい。
→ 求める寸法の分散値は各寸法の分散値の和に等しい
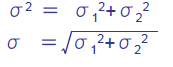
となり、全体の分散や標準偏差は、各部品の分散の和で求めることができます。
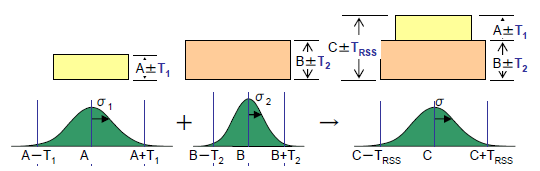
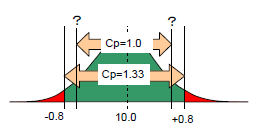
ここで「工程能力指数」の説明の中の、「標準偏差と公差域の関係」に示した通り、全ての寸法の工程能力指数を統一させて計算することで、片側の公差域を標準偏差の 倍数として表すことが出来ます。
![]()
そして、分散や標準偏差の式に上記式を代入することで、分散の式を公差の式に置き換えて、統計ばらつきを算出する事が出来るようになります。