幾何公差入門
幾何公差とは?寸法公差との違いや記号の種類、記載ルールを解説
幾何公差が必要な3つの理由、幾何公差の分類と種類のほか、幾何公差の記入ルールを詳しく解説
幾何公差とは、簡単に言うと形状や位置関係などの誤差の許容範囲を指示して規定するものです。
日本国内で主に使われている寸法公差は、サイズや長さの許容差を指示して規定するものです。形状や位置関係、測定の基準など細かな指示ができず、設計者の意図が伝えにくいデメリットがあります。
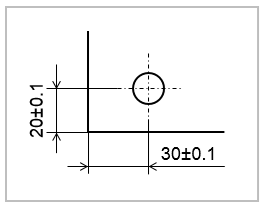
日本国内(寸法公差)
一方で、幾何公差は形状や位置関係など細かく指示でき、設計者の意図を明確に伝えられるところが特徴です。表記ルールに従い表記することで、サイズや長さだけでなく、円の中心位置なども明確に指示できます。そのため、設計者の意図を正しく伝えることができ、想定通りの加工や検査ができます。
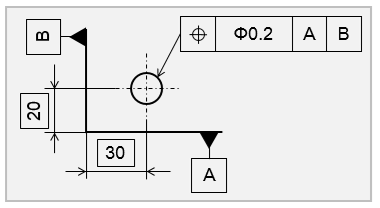
海外など(幾何公差)
幾何公差を使うには、表記ルールや指示の意図などを正しく理解する必要があります。この記事では、幾何公差の概要や種類、寸法公差との違いや表記ルールなどを詳しく解説していきます。
この記事を読むと分かること
この記事を最後まで読むことで「幾何公差とはどのようなものか」が把握でき、本格的に導入を検討できるようになるはずです。幾何公差を導入する動きは海外だけでなく国内でも広がっているので、しっかり理解しておくことをお勧めします。

本ページの内容を PDF でじっくりお読みになりたい方へ
「幾何公差入門」PDF にて無料公開中!
1.幾何公差とは

冒頭でも述べたように、幾何公差は形状や姿勢、位置関係などの誤差の許容範囲を指示して規定するものです。
JIS(日本産業規格)ではJIS B 0021にて「製品の幾何特性仕様(GPS)-幾何公差表示方式-形状,姿勢,位置及び振れの公差表示方式」にて幾何公差に関する概要が定義されています。GPS(Geometrical Product Specification)とは形状や姿勢、位置関係などのことで、公差は誤差の許容範囲を指します。
後ほど紹介する寸法公差は長さや角度の誤差を規定しますが、幾何公差は立体的なイメージで、形状の崩れ具合や傾き、回転体の振れなどの誤差を規定できるところが特徴です。
2.寸法公差(サイズ公差)との違い
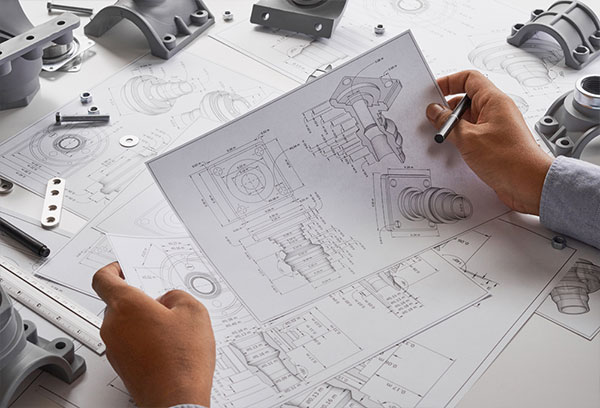
寸法公差とは、簡単に言うと基準寸法に対して許容できる範囲を指示し規定することです。例えば、基準寸法を100mmとした場合、いくら精度の高い技術でも100mm丁度に仕上げることは難しいです。
そこでどれくらいの誤差であれば品質や性能に問題がないのか検討し、誤差の範囲を指示するのが寸法公差です。
寸法の誤差が許容できる上限を最大許容寸法、下限を最小許容寸法と呼び、それぞれ下記のように基準寸法からの差(許容差)で指示します。下記の図の場合は、基準寸法が100で、最大許容寸法が100.5(+0.5)まで、最小許容寸法が99.6(-0.4)まで許容されていることになります。

このように、サイズや長さ、その他角度の許容差を指示できるのが寸法公差の特徴です。幾何公差と寸法公差の2つが理解できたところで、両者の大きな違いとしては次の2つがあります。
2-1.規制できる公差の範囲
幾何公差と寸法公差では、規制できる公差の範囲が異なります。下記は、幾何公差と寸法公差を比較した図面です。
左側で記載されている寸法公差は、長さと厚みの許容範囲を指示しています。寸法公差さえ見ればサイズ感は把握できますが、図形の形状までは規制されません。
そこで、右側の幾何公差での指示を見てみると、寸法公差に加えて平面度(どれだけ平らな面であるべきか)や基準面に対する平行度(2つの直線や平面が平行であること)が規定され、具体的にどのような形状が求められているのか明確に理解できます。
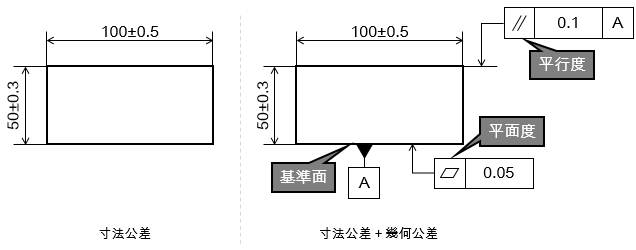
同じように、下記の左側の図は寸法公差のみ指示がされている円の図形です。寸法公差の指示で直径のサイズや誤差の許容範囲は分かりますが、詳しい形状は把握できません。右側の図のように誤差の範囲内で複雑に歪んでいたり、中心がずれた円になっていたりする可能性があります。

寸法公差はあくまでもサイズや長さ、角度しか指示できないため、形状や姿勢、位置関係に関しては都合よく解釈できてしまいます。その部分まで細かく指定し「理想とする形状がどのようなものなのか」、図面上で把握できるようにするのが幾何公差です。
| 寸法公差 | 幾何公差 |
|---|---|
| サイズ・長さ・角度 | 形状・姿勢・位置関係など |
2-2.測定方法の違い
寸法公差と幾何公差では、測定方法が異なります。長さの場合、寸法公差は基本的に2点間測定が原則で、長さであれば「2点間の長さ」に対する公差しか指示できません。
- 湾曲した形状
- 変形した形状
などは、寸法公差で細かく指示することが難しく、曖昧な解釈を残した状態になります。
一方で、幾何公差は明確な基準のもとに測定されます。ルールに従って形状や姿勢、位置関係などが細かく指定されているので、解釈が一定になるところが特徴です。
| 寸法公差 | 幾何公差 |
|---|---|
| 2点間測定 | 明確な基準をもとにルールに従って測定 |
| 解釈に差が出る | 基準が明確なので解釈が一定 |
幾何公差と寸法公差の違いが把握できたところで、なぜ幾何公差が必要なのか理由を見ていきましょう。
3.幾何公差が必要な3つの理由

- 寸法公差では指示できない設計者の意図を伝えられる
- 諸外国でも通用する図面が描ける
- 寸法公差から幾何公差にシフトする動きが出ている
3-1.寸法公差では指示できない設計者の意図を伝えられる
1つ目の理由は「2.寸法公差(サイズ公差)との違い」でも解説しましたが、幾何公差を使うことで設計者の意図が細かく伝えられることです。例えば先ほどの例の様に、寸法公差で下記のような指示をしたとしましょう。
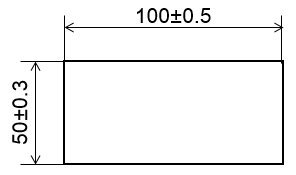
厚みや長さの公差は指示できますが、具体的な形状は規定できません。もしかしたら、下記のように表面が凸凹になっているかもしれません。

寸法公差の場合は表面に凸凹があっても斜めになっていても、2点間の距離が公差内に入っていれば良いことになります。
このように、寸法公差だけでは設計者の意図とは異なる形状となってしまう可能性があるのです。ここに幾何公差を加えて指示をすると、平面度(どれだけ平らな面であるべきか)や平行度(基準となる平面や直線に対する平行性)のように、どのような形状や姿勢が必要なのか詳しく指示できます。
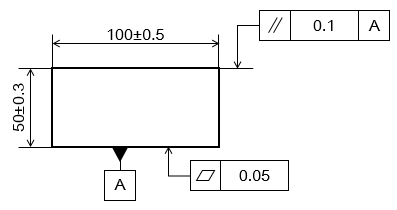
図面をもとに製造や加工をする側も具体的な仕上がりがイメージできるようになるため、設計者の意図を汲み取りやすくなります。その結果、設計側と生産側との間で認識のずれが起こりにくく、効率よく納得できる製品を完成させられるようになるでしょう。
3-2.諸外国でも通用する図面が書ける
2つ目は、諸外国に通用する図面が書けるようになることです。日本では製造現場で図面から意図を汲み取り、今までの知識や技術で加工をする寸法公差が使用されてきました。
しかし、欧米諸国の製造現場では、幾何公差が多用されている場面も少なくありません。そのため、海外企業に発注をするときに思ったように指示が伝わらず、予期せぬ品質トラブルが起こる事例が増えています。つまり、グローバル化に対応するには、幾何公差で指示ができるスキルが必須なのです。
先ほども解説したように、幾何公差では形状や姿勢、位置関係を細かく指示でき、誰が見ても同じように理解ができます。そのため、国を越えて図面を共有しても解釈が異なることがありません。
日本産業規格のJIS B 0420-1:2016「製品の幾何特性仕様(GPS)-寸法の公差表示方式-第1部:長さに関わるサイズ」の解説では「現状の多くの日本の図面では、決して欧米諸国などの技術者には理解されないものになってしまう」と警鐘を鳴らしています。このように、グローバルに活躍するためには幾何公差で読み書きできる技術が必要となってきています。
3-3.寸法公差から幾何公差にシフトする動きが出ている
3つ目は、日本国内でもグローバル化に対応できるように、寸法公差から幾何公差にシフトする動きが出ていることです。それを顕著に表しているのが、JIS規格の改訂です。2016年での改訂では、長さについては「形体の大きさ(サイズ)を指示するときのみ寸法公差を使用する」とも位置付けています。それ以外の場合は「幾何公差での指示」を行い、積極的に幾何公差を利用するよう促しています。
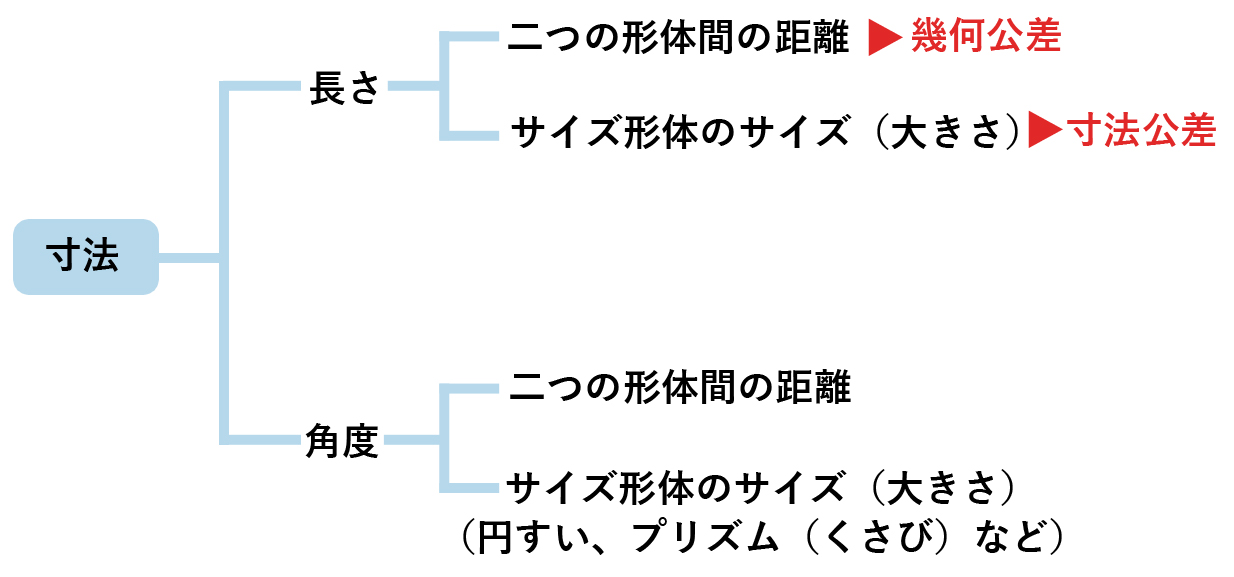
また、JEITA(電子情報技術産業協会)をはじめとする業界団体も同様に、幾何公差の考え方を取り入れた規格を定めるなど、この動きは活発化し始めています。
少しでも早く幾何公差を使えるようになることで、時代の流れに合わせたシフトチェンジができるだけでなく、競合他社に差を付けられるようになるでしょう。
幾何公差の必要性や幾何公差図面での公差解析のポイントについてもう少し詳しく知りたい方は、「幾何公差道場」にて幾何公差の必要性を詳しく解説しています。
基礎編
4.幾何公差の分類と種類

幾何公差は、下記の4つの分類に分かれています。
| 幾何公差の分類 | |
|---|---|
| 形状公差 | 対象形体の基本的な形状を規定する幾何公差 |
| 姿勢公差 | 基準に対しその形体の姿勢を規定する幾何公差 |
| 位置公差 | 基準に対しその形体の位置を規定する幾何公差 |
| 振れ公差 | 回転軸を中心に対象物を回転させたときにその形体の振れを規定する幾何公差 |
形体に規定する内容により、どのような幾何公差を指示するのかが異なります。幾何公差を指示するために必要な記号や指示方法の事例を踏まえて紹介するので、ぜひ参考にしてみてください。
4-1.形状公差
形状公差とは、対象形体の形状自体のばらつき範囲を規制する幾何公差です。データムを必要とせず、単独で形状を指示できます。
| 形状公差(データム不要) | ||
|---|---|---|
| 真直度 |  |
どれだけ真っ直ぐであるべきか指定する |
| 平面度 |  |
どれだけ平らな面であるべきか指定する |
| 真円度 |  |
どれだけ正確な円形であるべきか指定する |
| 円筒度 |  |
どれだけ正確な円筒形であるべきか指定する |
| 線の輪郭度 (形状公差) |
 |
断面内での線分が意図どおりの形状になるよう、輪郭線の歪みを指定する |
| 面の輪郭度 (形状公差) |
 |
面が意図どおりの形状になるよう、輪郭面の歪みを指定する |
データムとは、指定された幾何公差に基づいて加工や測定をする場合に、基準となる面や線、点などを指します。データムを指示することで基準が明確になり、加工や測定方法がしっかりと伝わります。
データムの意味や使い方については「5-3.データム記号を記入する」で詳しく解説しているので、参考にしてみてください。
また、データムの意味やデータムの優先度、また3平面データム系については「幾何公差道場」でも詳しく解説しています。
基礎編
4-1-1.真直度
真直度は「どれだけ真っ直ぐであるべきか」を指定します。面全体ではなく直線要素に対して適用されるところが特徴で、面内の直線要素や母線、中心線の曲がりなどを規制します。長尺物の反りの許容値を規制する場合などにも使われます。
| 真直度 | |
|---|---|
 |
|
| JISの意図 | 平行な2直線や平行2平面、円筒の公差域内(公差値にφがある場合)に直線成分がおさまること |
| 特徴 | 面全体ではなく、直線要素に対する真っ直ぐさを規制する |
| 事例 | 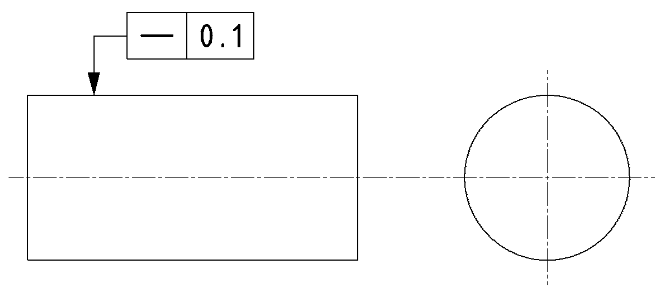 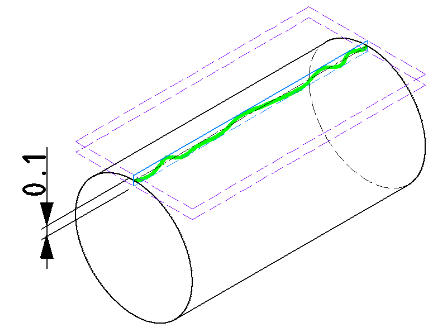
直線成分の真っすぐさを指示することで、反りや歪みを規制します。 |
4-1-2.平面度
平面度は「どれだけ平らな面であるべきか」を指定します。どれだけ厳密に加工をしても、平面には凹凸が発生します。
平面度を指定すると、最も凸の部分と最も凹の部分が公差幅の2平面間の間におさまらなければなりません。面の凹凸を抑えたい場合に指示します。
| 平面度 | |
|---|---|
 |
|
| JISの意図 | 平行2平面の公差域内に平面がおさまること |
| 特徴 | 平面内での反りや凹凸を規制する |
| 事例 | 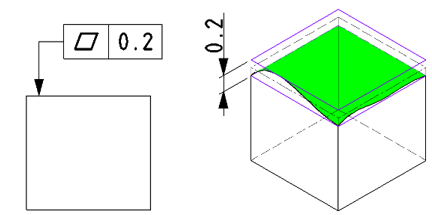
平面の歪みが平行2平面内おさまるよう、反りや凹凸を規制します。 |
4-1-3.真円度
真円度は「どれだけ正確な円形であるべきか」を指定します。冒頭の「1.幾何公差とは」でも解説したように、寸法公差では断面内での円の歪み具合までは指定できません。真円度を指定することで「どれだけ正確な円でなければならないか」を指示できます。
| 真円度 | |
|---|---|
 |
|
| JISの意図 | 対象とする断面内において、同軸で公差幅の円内に円形状がおさまること |
| 特徴 | 断面内の円形状を規制する |
| 事例 | 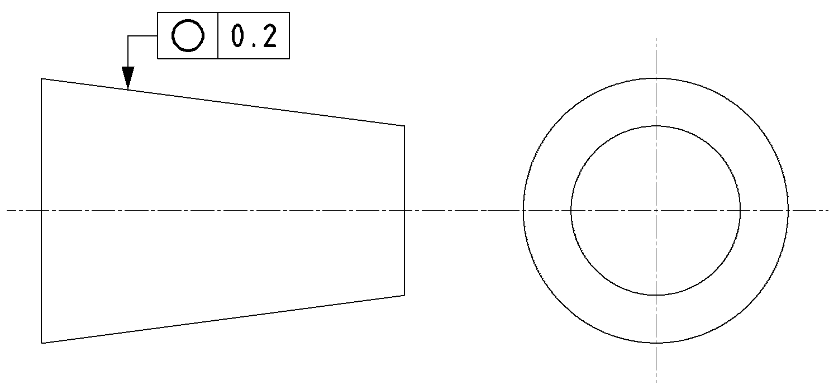 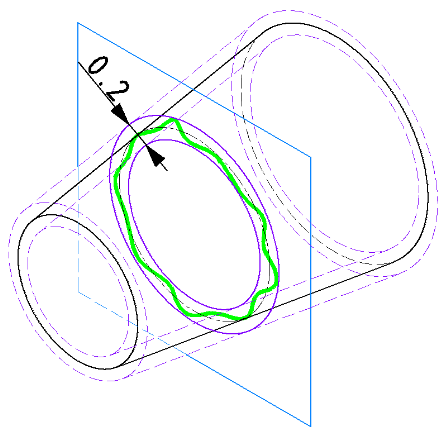
断面内での円形状の歪み具合を規制します。 |
4-1-4.円筒度
円筒度は「どれだけ正確な円筒形であるべきか」を指定します。円筒度は「真円度」と「真直度」の意味が含まれ、どれだけ正確な円形でどれだけ真っ直ぐであるべきかが規制され、円筒形体の歪みや反りなどを指示できます。
| 円筒度 | |
|---|---|
 |
|
| JISの意図 | 円筒面において、同軸で公差幅の円筒内に円筒形状がおさまること |
| 特徴 | 円筒形体の任意の断面における円形状と円筒面の全体の歪みを規制する |
| 事例 | 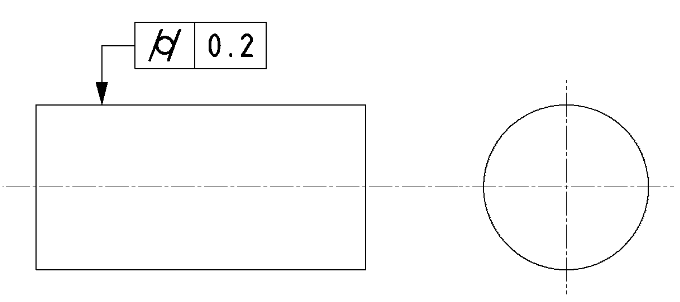 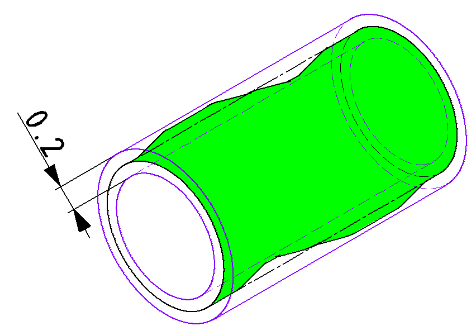
円筒面全体での歪みや反りを規制します。 |
4-1-5.線の輪郭度
形状公差での線の輪郭度は「輪郭線の歪み」を規制します。意図したとおりの輪郭線となるよう、輪郭線の歪み具合を指示します。
| 線の輪郭度(形状公差) | |
|---|---|
 |
|
| JISの意図 | 理論的に正確な寸法や形状に沿った2つの包絡線内に輪郭線がおさまること (2つの包絡線:公差値と同じ直径の円が正確な輪郭線に沿って動いた際の幅) |
| 特徴 | 断面内での輪郭線の歪みを規制する |
| 事例 | 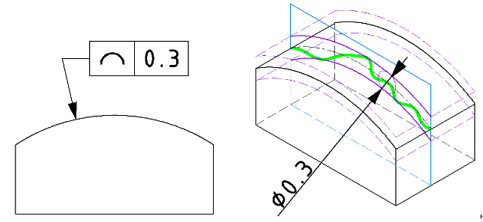
指示された方向の断面内において、輪郭線の歪みを規制します。 |
4-1-6.面の輪郭度
形状公差での面の輪郭度は「輪郭面の歪み」を規制します。線の輪郭度とは異なり、指定した面全体が対象となります。意図したとおりの輪郭面となるよう、輪郭面の歪み具合を指示します。
| 面の輪郭度(形状公差) | |
|---|---|
 |
|
| JISの意図 | 理論的に正確な寸法や形状に沿った2つの包絡面内に輪郭面がおさまること (2つの包絡面:公差値と同じ直径の球が正確な輪郭線に沿って動いた際の幅) |
| 特徴 | 面内での輪郭面の歪みを指定する |
| 事例 | 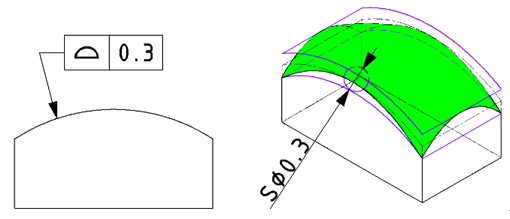
指示された面内において、輪郭面の歪みを規制します。 |
4-2.姿勢公差
姿勢公差とは、ある基準に対しその形体のあるべき姿勢の範囲を規定する公差です。基準となるデータムが必要な幾何公差で、以下の3つが当てはまります。
| 姿勢公差(データム必要) | ||
|---|---|---|
| 平行度 |  |
基準となる平面や直線に対してどれだけ平行であるべきか指定する |
| 直角度 |  |
基準となる平面や直線に対してどれだけ直角であるべきか指定する |
| 傾斜度 |  |
基準となる平面や直線に対してどれだけ指定の角度であるべきか指定する |
4-2-1.平行度
平行度は「基準に対してどれだけ平行であるべきか」を指定します。平面度は単独の平面を指すのに対し、平行度は基準となる直線や平面が存在します。
| 平行度 | |
|---|---|
 |
|
| JISの意図 | データム直線やデータム平面に対して平行な直線または平行な平面が、 公差幅の平行2平面または公差幅の円内(公差値にφがある場合)におさまること |
| 特徴 | 2つの直線や平面の平行性を規制する |
| 事例 | 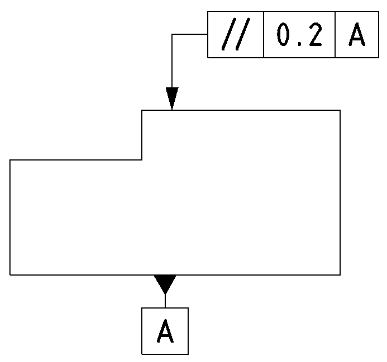 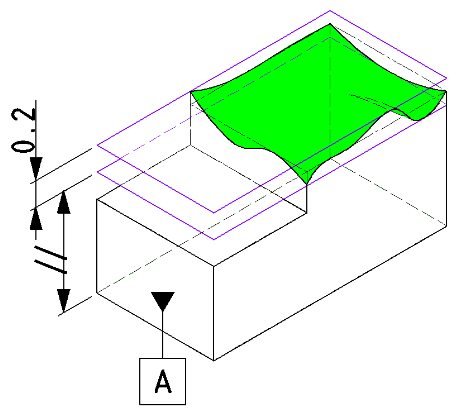
基準に対しての平行性を規制します。 |
4-2-2.直角度
直角度は「基準に対してどれだけ直角であるべきか」を指定します。直角度は角度で指定するのではなく、指示された形体が収まらなければいけない範囲(平行な2平面間の距離や円筒域)で指定をします。
| 直角度 | |
|---|---|
 |
|
| JISの意図 | データム直線やデータム平面に対して直角な直線または直角な平面が、公差幅の平行2平面または公差幅の円内(公差値にφがある場合)におさまること |
| 特徴 | 2つの直線や平面の直角性を規制する |
| 事例 | 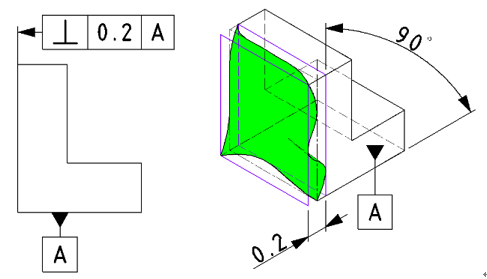
基準に対しての直角性を規制します。 |
4-2-3.傾斜度
傾斜度では「基準に対してどれだけ指定の角度であるべきか」を指定します。指定する形体は、基準に対して平行や直角ではない角度の形体が対象となります。直角度と同様に角度で指定するのではなく、指示された形体が収まらなければいけない範囲(平行な2平面間の距離や円筒域)で指定します。
| 傾斜度 | |
|---|---|
 |
|
| JISの意図 | データム直線やデータム平面に対して所定の角度の直線または平面が、公差幅の平行2平面または公差幅の円内(公差値にφがある場合)におさまること |
| 特徴 | 2つの直線や平面の傾きを規制する(平行や直角以外) |
| 事例 | 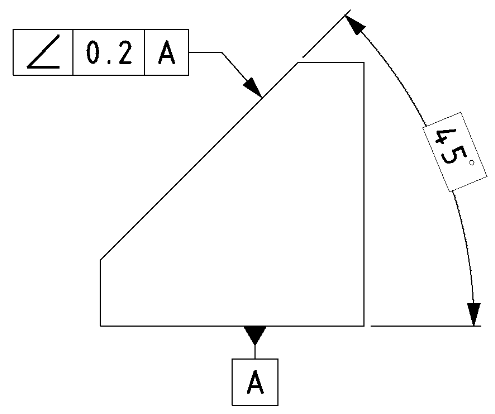 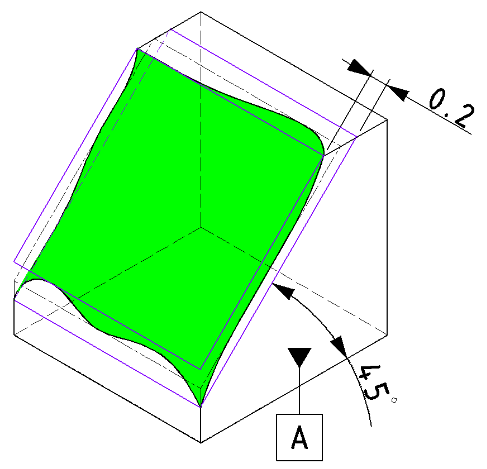
基準に対して指定されている角度からの傾きを規制します。 |
4-3.位置公差
位置公差とは、ある基準に対しその形体のあるべき位置の範囲を規定する幾何公差です。形状や姿勢を含めた位置関係を規制します。基準となるデータムが必要な幾何公差で、以下の6つが当てはまります。
| 位置公差(データム必要) | ||
|---|---|---|
| 位置度 |  |
基準に対してどれだけ正確な位置にあるべきか指定する |
| 同軸度 |  |
基準に対して同軸な円筒軸がどれだけ同軸であるべきか指定する |
| 同心度 |  |
基準に対して同心な円筒中心がどれだけ同心であるべきか指定する |
| 対称度 |  |
基準に対して対称形体の中心がどれだけ正確な位置にあるべきか指定する |
| 線の輪郭度 (位置公差) |
 |
基準に対して輪郭線がどれだけ正確な位置にあるべきか指定する |
| 面の輪郭度 (位置公差) |
 |
基準に対して輪郭面がどれだけ正確な位置にあるべきか指定する |
4-3-1.位置度
位置度は「基準に対してどれだけ正確な位置にあるべきか」を指定します。穴やボスの位置を指定する以外にも、面の位置などを指定する場合にも使えます。
| 位置度 | |
|---|---|
 |
|
| JISの意図 | データムに対して対象となる点や直線または平面形体が、理論的に正確な位置から公差の範囲内におさまること |
| 特徴 | 点や線、中心軸や中心面のほか、平面の位置を規制する |
| 事例 | 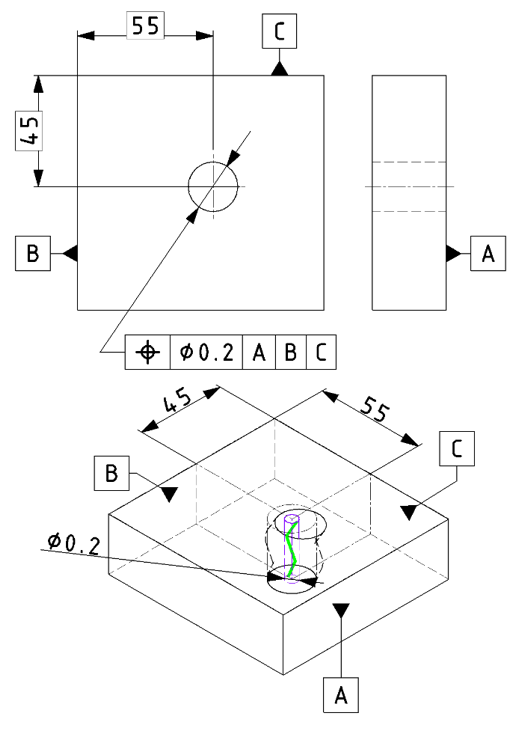
基準に対し、対象となる形体(点、線、面など)の位置などを規制します。 ※形状や姿勢も含む(対象となる形体による)。 |
4-3-2.同軸度
同軸度は「基準に対して同軸な円筒軸がどれだけ同軸であるべきか」を指定します。円筒形状どうしの軸のズレや傾きを規制したいときに使います。
| 同軸度 | |
|---|---|
 |
|
| JISの意図 | データム軸に対して同一軸上の対象となる軸が、公差の範囲内におさまること |
| 特徴 | 2つの円筒軸の同軸性を規制する |
| 事例 | 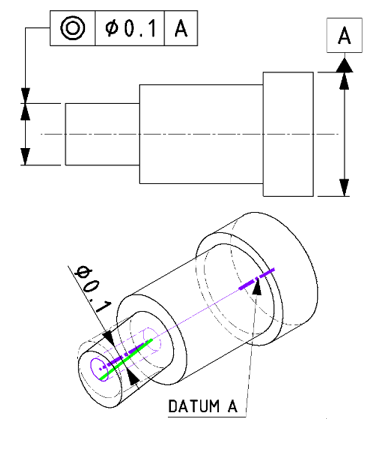
基準の軸に対し、対象となる軸の位置を規制します。※形状や姿勢も含む。 |
4-3-3.同心度
同心度は「基準に対して同軸上にある中心点がどれだけ同心であるべきか」を指定します。同軸度は軸を規制するのに対し、同心度は中心点を規制するところが違います。
| 同心度 | |
|---|---|
 |
|
| JISの意図 | データム軸やデータム点に対して同一軸上の対象となる中心点が、公差の範囲内におさまること |
| 特徴 | 2つの円筒中心のズレを規制する |
| 事例 | 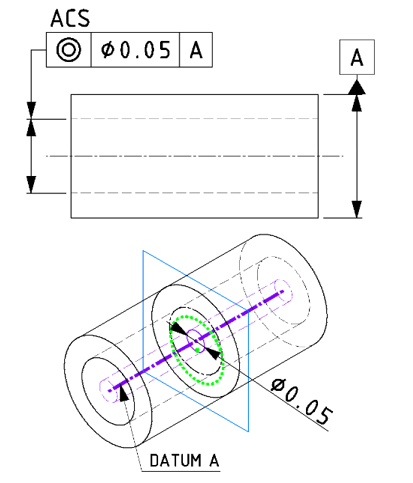
基準の軸や中心点に対し、対象となる形体中心の位置を規制します。 ※同軸度と混同する可能性がある場合は、公差記入枠周辺に「各横断面」もしくは「ACS」(Any Cross Section)を記載。 |
4-3-4.対称度
対称度は「基準に対して対称な形体の中心などがどれだけ正確な位置にあるべきか」を指定します。2面幅など、対称形体の位置や姿勢を規制したいときに使います。
| 対称度 | |
|---|---|
 |
|
| JISの意図 | データムに対して互いに対称である形体の中心面が、公差の範囲内におさまること |
| 特徴 | 基準となる平面や直線に対して、対称形体の中心位置のズレや傾きを規制する |
| 事例 | 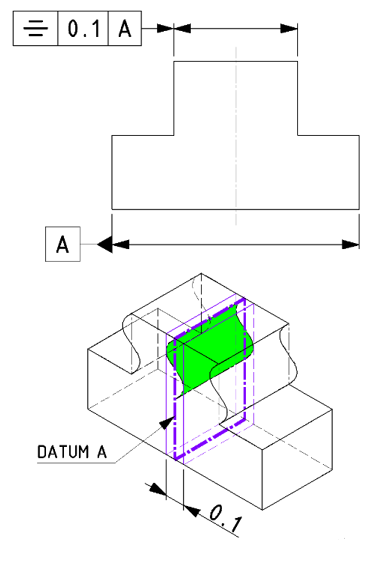
基準となる平面や軸に対して、対象形体の中心位置などを規制します。※形状や姿勢も含む。 |
4-3-5.線の輪郭度
線の輪郭度は「基準に対して輪郭線がどれだけ正確な位置にあるべきか」を指定します。形状公差での「線の輪郭度」とは異なり、データムを用いて「基準となる位置に対するズレ」などを指示します。
| 線の輪郭度(位置公差) | |
|---|---|
 |
|
| JISの意図 | データムに対して、対象となる輪郭線が理論的に正確な位置に沿った2つの包絡線内におさまること (2つの包絡線:公差値と同じ直径の円が正確な輪郭線に沿って動いた際の幅) |
| 特徴 | 基準からの正確な位置に対して、輪郭線のズレや傾きを規制する |
| 事例 | 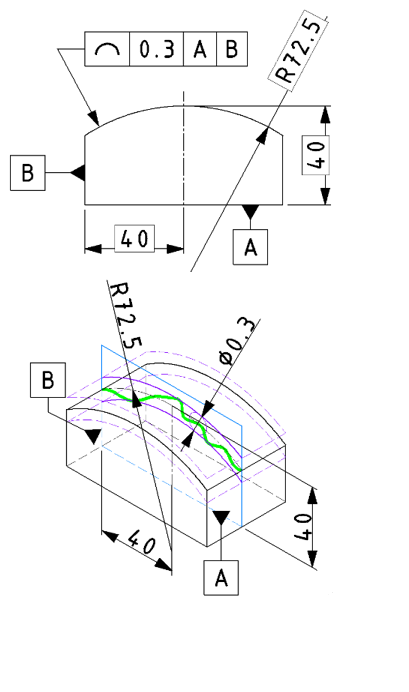
基準に対し、対象となる輪郭線の位置を規制します。※形状や姿勢も含む。 |
4-3-6.面の輪郭度
面の輪郭度は「基準に対して輪郭面がどれだけ正確な位置にあるべきか」を指定します。形状公差での「面の輪郭度」とは異なり、データムを用いて「基準となる位置に対するズレ」などを指示します。
| 面の輪郭度(位置公差) | |
|---|---|
 |
|
| JISの意図 | データムに対して、対象となる輪郭面が理論的に正確な位置に沿った2つの包絡面内におさまること (2つの包絡面:公差値と同じ直径の球が正確な輪郭面に沿って動いた際の幅) |
| 特徴 | 基準からの正確な位置に対して、輪郭面のズレや傾きを規制する |
| 事例 | 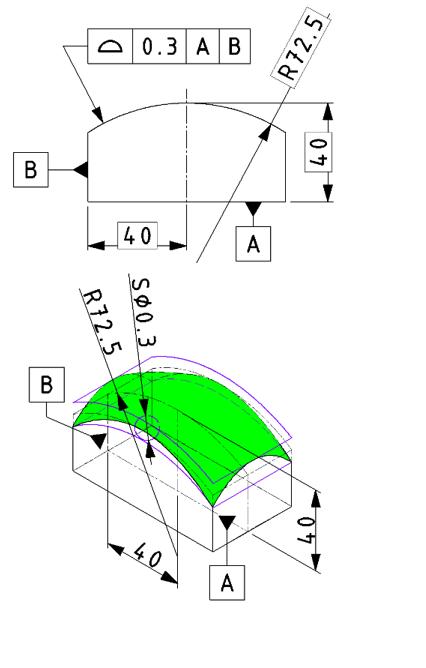
基準に対し、対象となる輪郭面の位置を規制します。※形状や姿勢も含む。 |
4-4.振れ公差
振れ公差とは、回転軸を中心に対象物を回転させたときに、その形体の振れの範囲を規定する幾何公差です。データムが必要な幾何公差で、以下の2つが当てはまります。
| 振れ公差(データム必要) | ||
|---|---|---|
| 円周振れ |  |
基準に対して部品を回転させた際の任意の円周上での振れを指定する |
| 全振れ |  |
基準に対して部品を回転させた際の表面全体の振れを指定する |
4-4-1.円周振れ
円周振れは「基準に対して部品を回転させた際の任意の円周上での振れ」を規制します。円周振れを判定する場合には、任意の円周上での振れ幅が公差内に入っていればOKですが、指定された形体範囲においては、どこで判定しても公差内に入っている必要はあります。
| 円周振れ | |
|---|---|
 |
|
| JISの意図 | データム軸まわりに回転させた際、対象となる形体面の任意の断面内での振れが公差の範囲内におさまること |
| 特徴 | 基本的に回転体に対して適用され、回転時の任意の円周上での振れを規制する |
| 事例 | 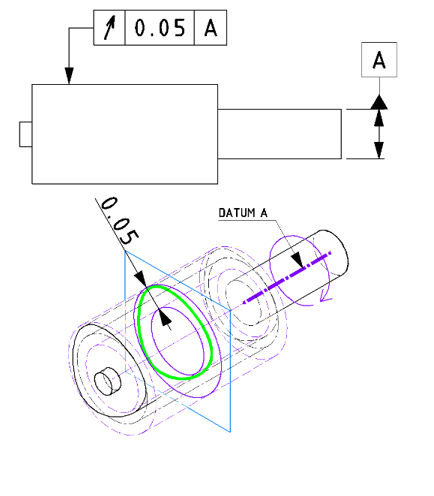
データム軸に対して回転させた場合の、任意の円周の振れを規制します。※形状や姿勢、位置のズレも含めた振れ量。 |
4-4-2.全振れ
全振れは「基準に対して部品を回転させた際の表面全体の振れ」を規制します。全振れの場合には、指示された面全体の振れ幅が「同一の公差範囲内」でなければなりません。
| 全振れ | |
|---|---|
 |
|
| JISの意図 | データム軸まわりに回転させた際、対象となる形体面全体の振れが同一の(一連の)公差範囲内におさまること |
| 特徴 | 基本的に回転体に対して適用され、回転時の形体面全体での振れを規制する |
| 事例 | 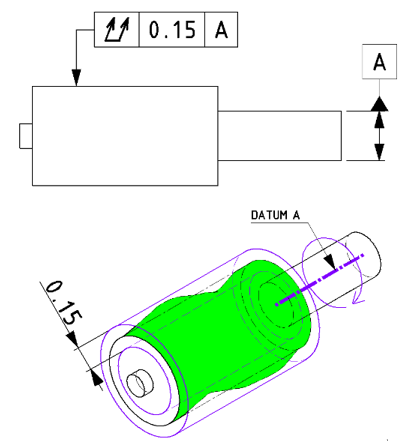
データム軸に対して回転させた場合の、対象面全体での振れを規制します。※形状や姿勢、位置のズレも含めた振れ量。 |

「幾何公差入門」PDF にて無料公開中!
5.幾何公差の記入ルール

幾何公差を指定するには、記入ルールを守る必要があります。幾何公差を記入するときには、幾何特性記号と許容値、データム記号の3つを指示します。(データム記号は形状公差の場合には不要)

それぞれどのように指示をするのか、詳しく解説していきます。
5-1.幾何特性記号
幾何特性記号とは、「4.幾何公差の分類と種類」で解説した幾何公差の分類を示す記号です。幾何公差を指示するときに一番左側の枠に記入し、どの幾何公差を指定するのか明確にします。
例えば、下記のような表記がある場合は、平面度の幾何公差を指定していることになります。

幾何公差は種類が多くて使い分けが難しそうと感じるかもしれませんが、すべての幾何公差が記号化されています。記号を記入するだけで、どのような幾何公差を指定しているのかしっかりと伝えられます。
5-2.許容値
幾何特性記号の隣には許容値を記入します。許容値とは公差値、つまり一番左側寸法の許容範囲で、具体的な数値で示します。下記の場合は、真円度の公差が0.05mm以内に収まることを指示しています。

機能を確保する為の精度や加工の難易度などを考慮しながら適切な許容値を記入することで、明確な判断基準ができ、許容範囲外の製品が出来てしまうのを避けることができます。
5-3.データム記号を記入する
データムとは、指定した幾何公差に基づき加工や寸法測定をする場合に、基準とする形体から得られる理想的な面や線、点などを指します。
例えば平行度の場合は、データム形体となる面や線などの形体を指定することで、指定した面や線と平行になるように加工や検査を行います。データムがないと基準とすべき面や線などが分からず、設計者の意図とは異なる加工や検査が行われる可能性があるのです。
その幾何公差が参照するデータムを、一番右の枠に大文字のアルファベットで記入します。

図面上ではどの形体がデータム形体に当たるのか指示するために、データム三角記号とデータムのアルファベットを記入して、指定したい面や線などを指示します。下記の場合は、下面をデータム形体として指示していることになります。
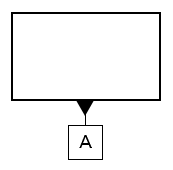
幾何公差の中でもデータムの指定が必要なのは、4-2.姿勢公差と4-3.位置公差、4-4.振れ公差です。これに該当する幾何公差の場合はデータムを記入して、基準となる面や線などを指定します。
5-3-1.データムに優先順位がある場合
参照するデータムを複数定義する場合は、優先順位の高い順に左側からアルファベットを記入します。下記の場合は、データムBを優先していることになります。

基本的にデータムの順位は、部品の組み立て順序や加工機への取り付け順序なども考慮して決めていきます。
5-4.図面指示の方法
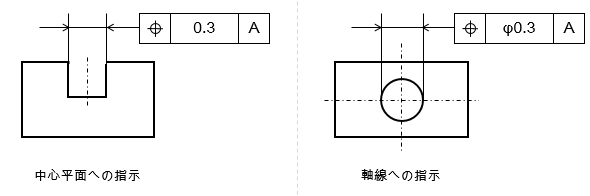
幾何公差の情報を図面上で指示する場合は、指示する面や線などに指示線を垂直にあてます。指示線と幾何公差記入枠を結ぶことで、どの箇所への指示なのか明確にできます。
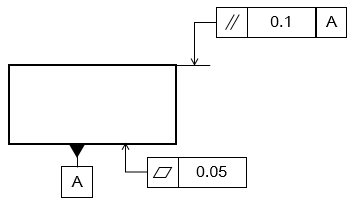
また、中心平面や軸線を対象に指示をする場合は、基本的には寸法線と一直線上に指示線を書きます。どちらの場合も幾何公差記入枠は図面に対して水平に配置するようにしましょう。
6.幾何公差の導入をサポートします

幾何公差を導入しようとした場合、知識の習得や現場での活用方法など、いろいろと課題が出てくると思います。
そこで、サイバネットシステムでは現状の課題把握や適切なゴールの設定などを行い、幾何公差が定着化できるようコンサルティングを実施しています。
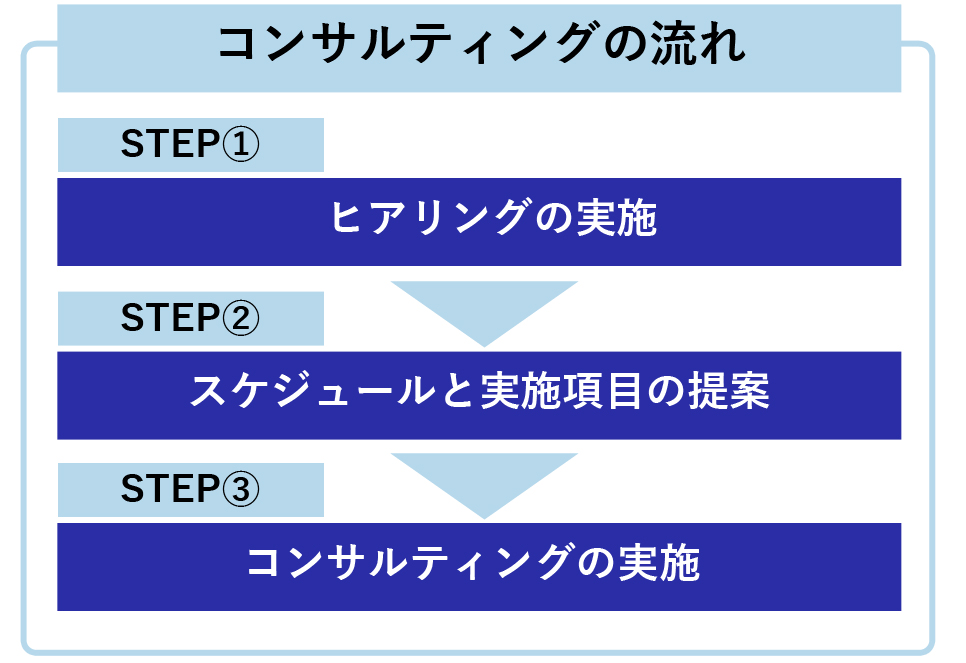
①ヒアリングの実施
現在の図面をもとに現状を把握して、課題やゴールの設定をします。コンサルティングの期間や対象となる人数など、幾何公差を導入するための基本的な情報をまとめていきます。
②スケジュールと実施項目の提案
ヒアリング内容をもとに、どのようなことを実践するのか具体的に提案します。
③コンサルティングの提供
スケジュールに沿って、幾何公差を導入するためのレクチャーなどを行います。
・図面を用いて実際に幾何公差を指示するスキルを身につける
・実践で使える適切な表現方法を覚える
・幾何公差の展開や定着方法をアドバイスする
など、状況に応じた方法でサポートさせていただきます。
幾何公差の習得を支援する教育やコンサルティングについて、もっと詳しく知りたい場合には下記より資料をダウンロードしてみてください。
7.まとめ
いかがでしたか?幾何公差とはどのようなものかを把握でき、本格的な導入に向けて参考にしていただけたかと思います。最後にこの記事の内容をまとめると、
◎幾何公差とは、形状や姿勢、位置関係などの誤差の許容範囲を指示して規制すること
◎寸法公差とは、基準寸法のみに対して許容できる範囲を示し規制すること
◎幾何公差と寸法公差の主な違いは次の2つ
1)規制できる公差の範囲:寸法公差はサイズや長さ、角度だけしか規制できず、幾何公差では形状や姿勢、位置関係など細かく規制できる
2)測定方法の違い:寸法公差は基本的に2点測定が原則、幾何公差では明確な基準のもと、ルールに従って測定される
◎幾何公差が必要な理由は次の3つ
1)寸法公差だけでは指示できない内容を細かく指定できるため、設計者の意図を伝えられる
2)欧米諸国は幾何公差が多用される場面も多く、諸外国でも通用する図面が必要になる
3)日本国内でも寸法公差から幾何公差にシフトする動きが出ている
◎幾何公差の分類と種類は下記のとおり
| 幾何公差の分類と種類 | ||
|---|---|---|
| 形状公差(データム不要) | ||
| 真直度 |  |
どれだけ真っ直ぐであるべきか指定する |
| 平面度 |  |
どれだけ平らな面であるべきか指定する |
| 真円度 |  |
どれだけ正確な円形であるべきか指定する |
| 円筒度 |  |
どれだけ正確な円筒形であるべきか指定する |
| 線の輪郭度 (形状公差) |
 |
断面内での線分が意図どおりの形状になるよう、輪郭線の歪みを指定する |
| 面の輪郭度 (形状公差) |
 |
面が意図どおりの形状になるよう、輪郭面の歪みを指定する |
| 姿勢公差(データム必要) | ||
| 平行度 |  |
基準となる平面や直線に対してどれだけ平行であるべきか指定する |
| 直角度 |  |
基準となる平面や直線に対してどれだけ直角であるべきか指定する |
| 傾斜度 |  |
基準となる平面や直線に対してどれだけ指定の角度であるべきか指定する |
| 位置公差(データム必要) | ||
| 位置度 |  |
基準に対してどれだけ正確な位置にあるべきか指定する |
| 同軸度 |  |
基準に対して同軸な円筒軸がどれだけ同軸であるべきか指定する |
| 同心度 |  |
基準に対して同心な円筒中心がどれだけ同心であるべきか指定する |
| 対称度 |  |
基準に対して対称形体の中心がどれだけ正確な位置にあるべきか指定する |
| 線の輪郭度 (位置公差) |
 |
基準に対して輪郭線がどれだけ正確な位置にあるべきか指定する |
| 面の輪郭度 (位置公差) |
 |
基準に対して輪郭面がどれだけ正確な位置にあるべきか指定する |
| 振れ公差(データム必要) | ||
| 円周振れ |  |
基準に対して部品を回転させた際の任意の円周上での振れを指定する |
| 全振れ |  |
基準に対して部品を回転させた際の表面全体の振れを指定する |
◎幾何公差を記入するときのルールは下記のとおり
1)一番左側に幾何公差の分類を示す幾何特性記号を記入する
2)幾何特性記号の右隣に寸法の許容範囲となる許容値を記入する
3)(姿勢や位置の幾何公差の場合には)一番右側に参照データムを記入する
データムの優先順位がある場合は、左側から優先順位順にアルファベットを記入する
この記事をもとに幾何公差を導入する必要性やメリットが把握でき、少しでもみなさまの幾何公差図面作成のお役にたてることを願っております。幾何公差の導入や教育でお困りの場合は、お気軽にお問い合わせください。

「幾何公差入門」PDF にて無料公開中!