公差の資料室/ダウンロード
その図面、まだ寸法公差で設計していませんか？
海外でも通用する幾何公差図面の実現に向けて
その図面、まだ寸法公差で設計していませんか？
海外でも通用する幾何公差図面の実現に向けて
貴社の図面は穴の位置や段差などが寸法公差で指示されていたり、あたかも1つの中心軸上にすべての軸が配置されていて、軸方向の位置がやはり寸法公差で指示されているなど、寸法公差がメインの図面になってはいないでしょうか？もちろん、寸法公差で指示できるものもありますが、公差の多くは「幾何公差で指示すべき公差」となっております。本講演資料では、図面の幾何公差化や、幾何公差図面における公差解析などについて、ご紹介します。
＊ 本資料はこちらのセミナーの講演資料です。
資料サンプル
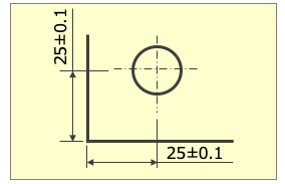
1.寸法公差の曖昧さ
寸法公差では基本的に「2点間計測で管理」されるため、「どこを基準に」「どのように寸法を測定するか」「人によっては解釈が異なる」など、寸法の定義が非常に曖昧になってしまうという問題を含んでいます。
一方、正しく定義された幾何公差図面では「基準が明確で解釈も一定」となるため、寸法公差図面のような「曖昧さによる問題」を防ぐことが出来ます。
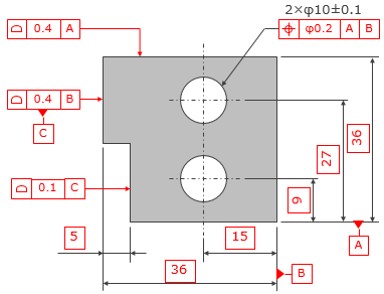
2.幾何公差で指示すべき例
「サイズ公差以外を幾何公差で指示した例」をご紹介します。各基準となる面をデータム形体A、B、Cとして設定し、□で囲まれた理論的に正確な寸法TED (テッド) で正確な位置を指示して、位置度や輪郭度の幾何公差で指示します。
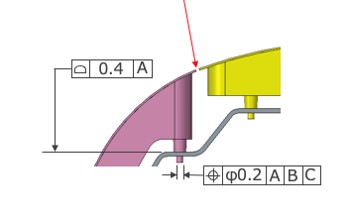
3.傾きの考慮
幾何公差図面における公差解析のポイントとして「傾きの考慮」があります。寸法公差図面でも同様に考慮しなければならないこともありますが、幾何公差図面では特に「幾何公差内での傾き」についての考慮が必要になる場面も多くあります。
関連する全ての寸法や公差を過不足なく抽出し、さらに「各寸法が変動した場合の影響度」も考慮して公差解析する必要があります。
＊続きはダウンロードしてお読みください。