CAEコラム
【解析講座】機械学習のためのCAE有効活用の考え方~物理現象、工学設計における応用事例~
筆者:近畿大学理工学部機械工学科 教授 和田 義孝 先生
目次
1. はじめに
深層学習、生成系AIなど機械学習にまつわる話題はここ10年事欠かない状況が続いています。CAEを活用している企業は実験計画法や回帰分析などの手法を使って現象の理解と設計や生産の改善を続けています。機械学習は、画像認識や文章生成ではなく実際の工学への適用も大いに期待されている状況は続いていると言えます。一方で、機械学習は使いたいけれども、どうしたら始められるのか、どのような量をデータとして学習させることができるのかなどハードルが高く感じる部分もあると思います。本稿では、機械学習の基礎から学習するためのデータとその量についてご紹介し、CAEを有効に利用するための考え方を紹介いたします。
2. 機械学習とは
画像認識に代表される文字認識、 人認識、 顔認識等のピクセル単位で学習するディープラーニング(=大規模入力、多階層のニューラルネットワーク)の成功から大規模な研究開発およびIT企業や自動車企業などによる投資が始まりました。 これらの動きに呼応する形で、 例えばGPUの開発元であるNVIDIA Corporationによるディープラーニング向けのライブラリの無償利用、 各研究機関や企業によるディープラーニング向けのAP(I Application Programming Interfaceの略称で、 具体的にはKeras、 PyTorchなどが Pythonで利用可能)の開発が加速しました。 つまり、 いつでもだれでも機械学習を始めることができる状態にあります。 もちろん、 知識は必要ですが始めるためのコストは極めて低いといえます。
インターネットには多くのチュートリアルや機械学習をやってみた個人の記事がいくらでも手に入る状態です。しかし、画像解析による応用事例は多数見受けられますが、物理現象、工学設計における応用事例は少なく、いまだ試行錯誤が続いています。 一方で、有償ではありますが、商用のサロゲートモデル(代替モデルのことで、利用範囲は限定されるが、 極めて高速に現象を予測することができるモデル)構築のためのソフトウェアも利用可能となっています。しかし、適切なパラメータ範囲でデータをどの程度準備したらよいのかなどは依然としてユーザに丸投げの状態です。少し前の報道になりますが、トヨタ自動車株式会社は、2019 年に自動運転実現のためには142 億万kmの走行距離が必要だという試算を示しています。この数値は、技術のある運転手一万人が一人あたり1万km以上の走行距離が必要であることを意味しています。 このような量のデータ収集は現実的ではなく、 データの総量を減らすための技術開発が機械学習の利用には強く求められているということでもあります。
機械学習とは、AIだけではなく、データドリブンな方法であり、単なる予測器(機械学習等によってつくられたモデルのことで、ここでは予測器と代替モデルは同じものを指す)を生成するだけではなく、物理現象も再現できる代替モデル構築まで可能な手法として期待されています。代替モデルはいくつかの手法により構築が可能です。
- 深層学習
- ガウス過程
- ベイズ学習
- 決定木
- スパースモデリング
などこれら以外にも重回帰などの古典的方法も含めれば構築可能な手法は多数あり、日々アルゴリズムの改良が行われています。機械学習はここ数年で急速に適用事例が増加した分野です。機械学習に関する手法の共通の目的は、時間のかかる順問題や逆問題のプロセスを高速化することです。 また、高速化自体が目的でない場合は、同定が困難なシステムの代替モデル構築が目的となります。
3. データの種類
データは数値化できるものであればどのようなものでもよく、
- 画像とタグ(種類を表す)
- 数値の組(工学で扱う計測や計算可能な整数や実数)
などが代表的なデータです。
分類はタグとして表現します。具体的には、タグの種類がn個あれば出力がn個あり、該当する出力にだけ有意な値(通常は1)が出力されます。波形などもFFTやウェーブレット変換などを経由すれば数値の組として利用可能です。連続したデータはサンプリング周波数を変更したり積分などの処理をしたりして離散的な数値に置き換えることが必要になります。この理由は、入力は動的に変更ができないため学習を始める前に入力の形態(ベクトル、マトリックスなのか、それらのサイズなど)を決める必要があるためです。
例として、ある物体の運動の様子を図1に示します。
これは加速度、速度、変位を表しています。このまま入力は難しいので、2.5msec毎にデータをサンプリングし直します。そうすると時間方向に24 点のサンプリング時刻が得られます。また、加速度は全体としての増減傾向は理解できますが、数値として表すとかなり変動が激しいこともわかります。問題にもよりますが、加速度を積分した速度やさらに積分した変位などを入力値として利用したほうが機械学習に適したデータになることがほとんどです。また、加速度が最も重要な因子である場合は、移動平均(着目した時刻の前後2 や3 つの時刻の値も使う)を取ることにより滑らかな加速度が得られます。データの前処理は有効です。まずはどういった特徴がデータにはあるのか、グラフなどを通じて確認することがよりよい学習に必要です。
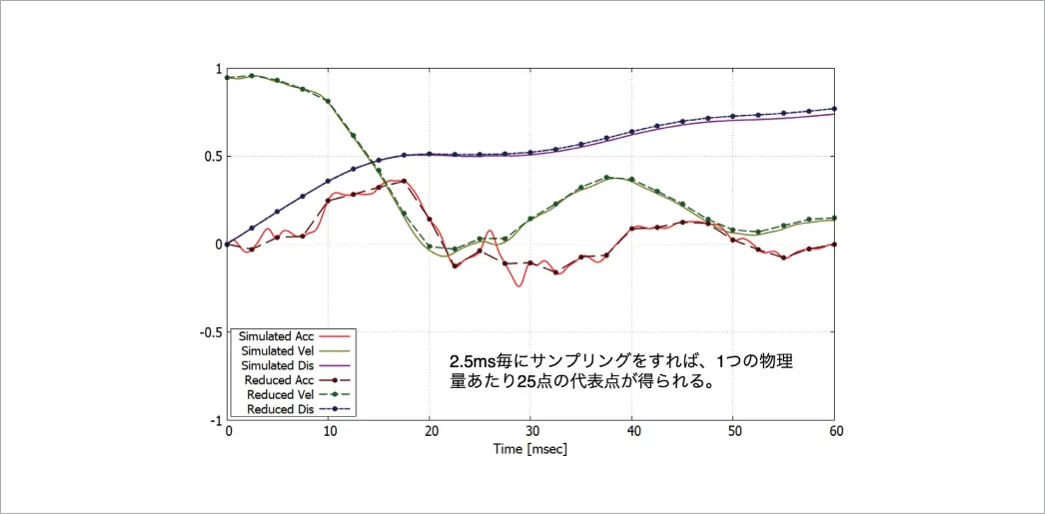
図1 データ抽出の例:加速度、速度、変位の再サンプリング
4. はじめてみよう ~ sin関数の例題~
ここでは、サイバネットが提供している総合CAE教育システム「CAEユニバーシティ」で私が担当している講座「機械学習によるCAE代替モデル構築 ~基礎から具体事例まで~」で、実際に行っているsin関数の予測を例に解説いたします。図2に示すように、CSV形式で入力となるxの値と、予測されるsin(x)の値の組がここでは201点あります。このデータは学習データ(training data)と呼びます。学習はこのデータによって行われます。学習データに含まれないデータは別途用意する必要があります。このデータは学習時に同時に評価します。このデータのことを検証データ(validation data)と呼びます。このデータもCSVファイルとして用意します。また、学習が終了した後に、もう一度だけ汎化性能(未学習のデータであっても予測が正しくできる性能)を調べるために上記の2つのデータに含まれないデータを使って評価します。このデータのことをテストデータ(test data)と呼びます。
学習を成立させるためにはいくつかの要件がありますが、少なくとも2~3 点では学習が成立しないことは明白です。しかし、たとえ201 点のデータがあっても、分布が偏っていたり、頂点(例えばx=0.25や0.75)近傍のデータが全くなかったりすれば、精度は期待できないでしょう。つまり、データの分布は予測精度そのものに影響を与えますが、すべてにおいて密である必要はありません。
とらえたい特徴を表現できる程度のデータの分布は必要と思ってください。一方で、そのような特徴もわからない場合は、しかたないので可能な限りデータを集めて学習が成立する可能性を高める努力が必要です。ある程度現象の傾向は理解しその理解に基づきデータを用意するかとにかく大量のデータを用意するという2 つの考えがあります。機械学習ではこの2 つの中間的な対応が求められているのだと考えています。
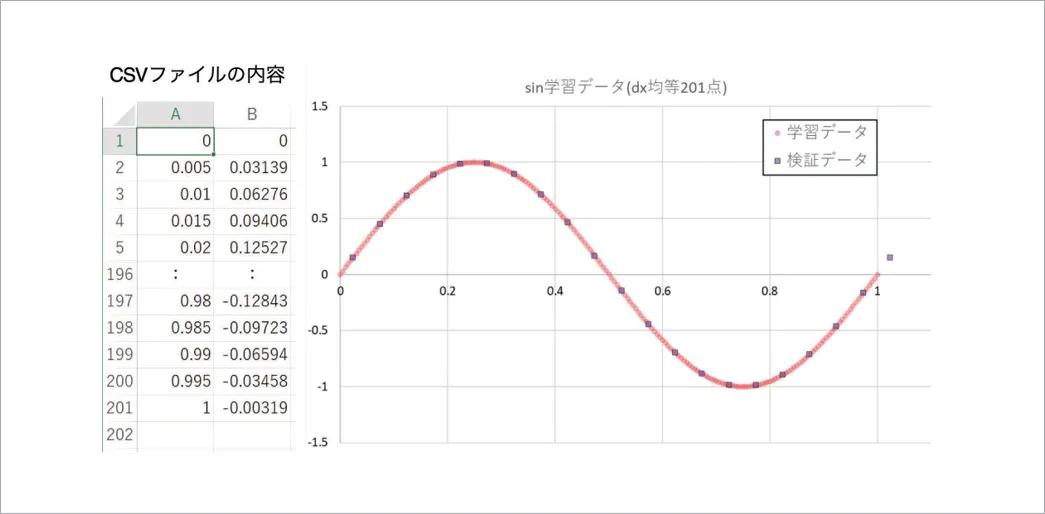
図2 sin関数の学習の例:CSVファイルに記述されたデータ、A列がx、B列がsin(2πx)を表す。xは正規化された値とし0 ~ 1
5. CAE活用のための考え方
図3にはある部品の評価点における応力の度数分布を示しています。前章で示したようにデータの特徴を捉えるようなデータの準備は必要であること述べました。一方で、これほど簡単な関数関係でないことがほとんどです。多入力であれば基本的にグラフ化は困難であると言えます。そこで、図3に示すような度数分布を通じてデータの傾向を理解してみましょう。データは十分に多く存在していると考えてください。そのような状態では予測したい値の近いデータが多ければ多いほど予測の精度は向上します。一方で、データがなければ予測は正しく行われません。同様に相対的に最頻値とくらべてほとんど存在しないデータの階級にある予測はできるのでしょうか。理想的にはできると言いたいところでしょうが、現実には、有限の時間内で学習を打ち切るため、精度は最頻値の階級に比べると予測精度は低くなります。
このような分布を持たないようにデータを作ることは可能でしょうか。一般には大変な困難が伴うことが予想されます。なぜならばここで示したデータは実験計画法を駆使して十分検討したパラメータの組み合わせの結果、このような分布になったからです。つまり、ランダムで一様になるような入力のパラメータの値の組が準備できたとしても、予測したい対象となる物理量は必ずこのような分布を持ってしまいます。また、正規分布にならないことも多いことは様々な分野で知られていることだと思います。材料強度の分野ではワイブル分布に従うことがよく知られています。我々はこのような不均一さを持つデータを対象とせざるを得ません。特にこういった分布の状況もわからない まま学習を行っても予測精度が高くなるかどうかやはりわからないと言えます。少なくともデータの頻度の差がなるべく少なくなるようなデータの準備は必要です。
CAEを用いれば、実験では計測困難なデータを取得することは可能です。また、パラメトリックに解析を自動実行することも容易だと言えます。物理問題の代替モデルを構築するには、CAEを活用しない手はありません。実験よりはるかに簡単に、データの取得が可能であるだけではなく、試行錯誤しながらのデータ取得も可能です。まさに、CAEの真骨頂だと言えます。CAEの解析を多数実行するのであれば、予測器の構築は結局コストが高いのではないか、ということはどなたも考えることです。しかし、よく考えてみてください。限定された現象ではありますが、1 秒未満で予測が終了するサロゲートモデルはモデルベース開発や1D-CAEの1 つのモジュールとしても活用できます。また、電卓やEXCELよりは性能が高い代替モデルという見方もできます。構築には確かに時間が必要です。しかし、その代替モデルが複数の人によって使われ、CAEよりも多くのケース数を評価するのであれば必ずどこかで損益分岐点が存在します。この判断は皆様が抱えている業務ごとに異なるので見極めるのは現場にいるあなたであると言えます。少なくともより効率的な評価方法が求められている現状において、CAE+機械学習の融合は強力なツールになると考えています。
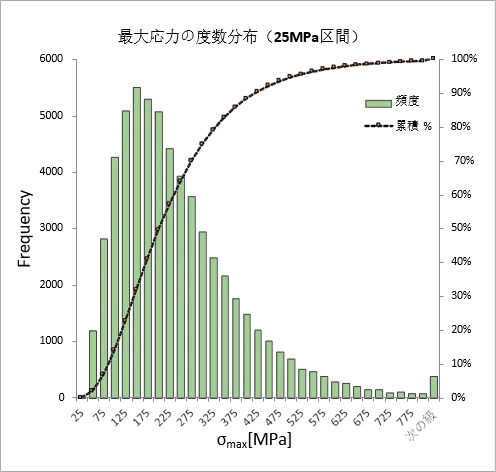
図3 機械部品応力評価結果:6万ケースの評価結果、実験計画法を用いて生成された入力パラメータを用いたがこのような分布を持つ
6. おわりに
高精度なCAEを代替するサロゲートモデルの構築にはもう少しの工夫と機械学習特有の技術について知識が必要になります。しかし、最も重要なことは、対象とする現象の領域知識(現象についての理解、専門知識)が必須です。
たとえば、ある因子の影響度が高いという知見や経験があれば、その因子を学習モデルの入力パラメータとして採用すべきです。また、変化が大きいところは多くの場合で評価対象になることが多いと思います。そういった個所のデータは特に準備すべきでしょう。こういったことが頻度の不均一さを解消し学習が成立しやすく、かつよりよい予測器の構築につながります。
構造解析において、静弾性解析は線形問題です。荷重に対して変位をはじめとする物理量は線形関係にあります。
しかし、機械学習でこの問題を学習させると線形ではありません。なぜならば、線形問題とわかっているなら、入力パラメータに荷重は通常入れません。その他の断面二次モーメントや荷重位置を入力パラメータにすべきでしょう。このようにある程度の汎用性を求めると線形問題だと思っていたものも意外に簡単ではない対象かもしれません。現象を見極め、基本に立ち返り、1 つずつ経験を獲得することが、CAEと機械学習の有効利用の近道だと強く感じています。前述のCAEユニバーシティの講座では、実習を行いつつ解説しているため、より深くご理解いただけると思います。興味をお持ちになりましたら、ぜひお問い合わせください。




