CAEを学ぶ
はじめてみよう!流体解析(入門編)[Ⅰ]
~流体解析はなぜ必要なのか~
はじめに
設計の詳細化、解析の高精度化に伴い、 流体解析 への関心が高まっています。Ansys社は
Ansys Fluent や Ansys CFX 、 Ansys Icepak といった汎用/専用流体解析ツールを提供しており、ツールを導入すればすぐにでも流体解析(CFD;Computational Fluid
Dynamics)を行うことが可能です。また、ハードウェア環境の飛躍的な進歩により、従来の環境では長時間に及ぶ解析も数分の一の時間で行うことが可能となっています。
このように、ソフトウェア、ハードウェアともにCFDを行う環境が整ってきていますが、実際の解析作業を始めようとしたとき、なかなか着手できない現状があります。その理由としては、流体力学に関する知識の不足や、CFD経験者の不在などが挙げられます。また、知識を身に付けるにしても流体力学の難解なイメージやCFD特有の用語が多いことが障害となっているようです。
弊社では、こういった点でお悩みのお客様を対象として「 はじめての流体解析体験セミナー 」を月1回、無料で開催しています(セミナーの詳細については本稿末尾を参照)。本稿ではセミナーの内容から核となる内容を取り出し、流体解析を始めるに当たって必ず押さえておきたい点について今後4回に渡ってご紹介致します。今回は流体解析の必要性、 構造解析 との違い、流体の基礎方程式の導出について取り上げます。後続の連載では レイノルズ数と乱流(第2回) 、 熱流体解析概要(第3回) 、 流体解析作業時のポイント(第4回) を予定しています。
流体解析はなぜ必要なのか
流体解析も他分野の解析と同様に、試作回数の低減や、解析による未知の現象の再現及び理解、得られた知見の新規製品開発への活用等が目的として挙げられます。ここではもう1つとして、流体解析ならではの解析精度の向上について具体例を挙げてご紹介致します。
ケース1:伝熱解析
伝熱解析では構造体のみモデリングし、構造体周囲を取り囲む流体との熱のやり取りに関しては熱伝達境界として考慮することが一般的です。具体的には熱伝達係数と雰囲気温度を入力しますが、熱伝達係数の値がよく問題になります。
熱伝達係数は一般に、構造体周囲の流体の物性値(密度、粘性率、熱伝導率など)、流れの状態、構造体表面の形状(凹凸など)等に依存するため、空間的な分布を持ちます。この熱伝達係数を見積る方法としては、(1)理論式、(2)実験による測定、(3)実験と解析結果の合わせ込みがあります。いずれの方法も本来局所的な分布を持つ熱伝達係数を求めることは困難で、伝熱解析を行う際はモデル全体で一定の値、または面ごとに異なる値(各面では一定)、といった簡単な条件にせざるを得ません。したがって、解析結果を評価する際は実際との条件のずれを考慮する必要があります。
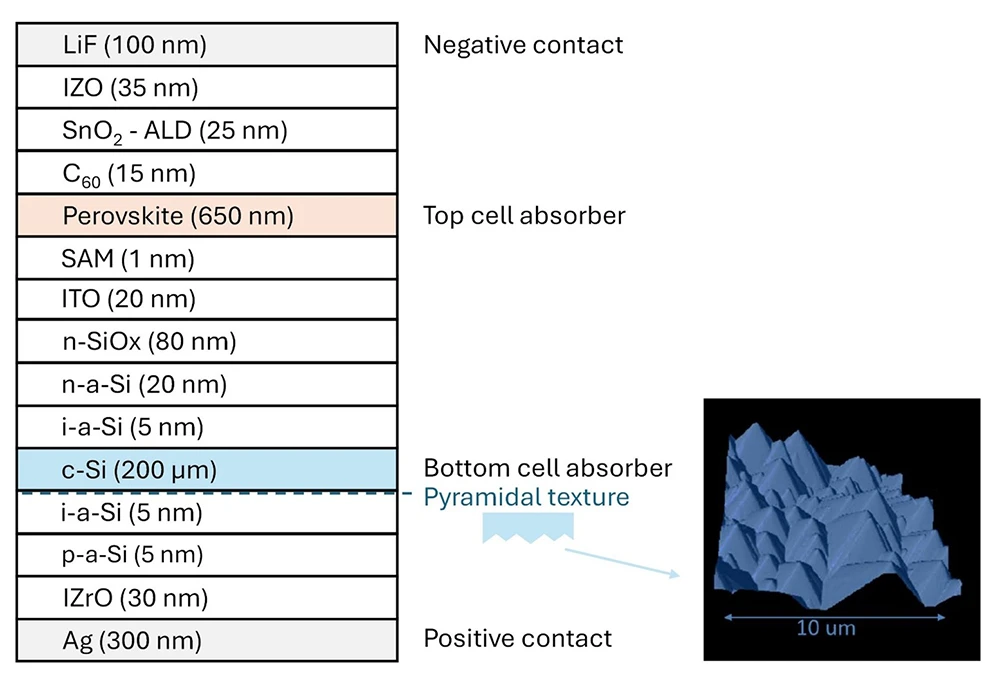
一方、熱流体解析では流れの影響を考慮した流体-構造体間の熱のやり取りを直接計算することが可能なため、伝熱解析で必要な熱伝達境界を定義する必要がありません。Ansys Workbench Mechanical(伝熱解析)、Ansys CFX(熱流体解析)によるLEDチップの解析例を図1に示します。伝熱解析では構造体表面の熱伝達係数を5W/m2K、雰囲気温度を20°Cとしています。熱流体解析では構造体周囲の流体領域をモデリングし、流体領域の外表面は20°Cの大気開放条件としています。両者の最大温度を比較すると熱流体解析の方が約17°C低いことがわかります。
ケース2:構造解析
構造解析では構造体が流体から受ける力(流体力)を圧力荷重または力荷重として定義する場合がありますが、構造体表面の流体力は流れの状態に依存し、局所的な分布を持ちます。熱伝達境界と同様に、流体力を面内で一定として定義した場合、本来の流体力分布と異なるため、結果評価の際は条件のずれを考慮する必要があります。Ansysでは流体力に関してもCFDツールから構造解析に転送することが可能なため、より実際に近い条件での結果を得ることが可能です。また、温度分布に関しても構造解析に転送し熱応力解析を行うことが可能です。
図2は、図1で得られた温度分布をAnsys Workbench Mechanicalに転送し熱応力解析を行った結果です。相当応力の最大値を見ると、
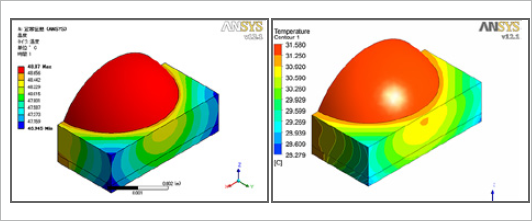
図1 LEDチップの温度分布
左図:伝熱解析、右図:熱流体解析
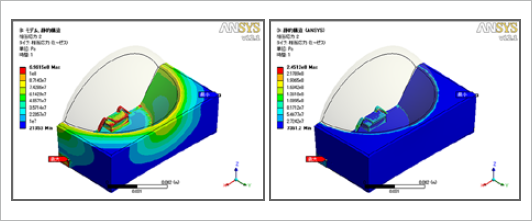
図2 LEDチップの相当応力分布
左図:伝熱解析、右図:熱流体解析の温度分布を転送
熱流体解析結果の温度が低いことに伴い、1/3程度の値となっています。
以上の2ケースから熱流体解析を考慮することにより解析の高精度化が可能であることがわかります。
構造解析と流体解析の違い
構造解析と流体解析とでは解析対象が異なることを初め、現象の記述方法、構成則、物性、現象の複雑さなど様々な点で異なりますが、ここではより直感的に違いを理解するため、構造体、流体に一定のせん断力を加えた場合について考えます。
構造体に外から一定のせん断応力を加えると、力が釣り合うまでせん断変形し、その後は静止状態になります。一方、流体にせん断応力を加えた場合はどこまでも変形を続け、せん断応力が無くなってはじめて静止します。構造体の変形量は流体と比較して非常に小さいため変形量で現象を記述する方法が適当ですが、流体の場合はせん断応力が働く限り際限なく変形するため、変形量による現象の記述が困難です。そのため、流体の変形を記述する際は変形量ではなく、変形速度、すなわち流速(速度)で現象を記述します。
応力が既知の場合、構造力学で応力-歪み関係から構造体の変形量が決まる(逆に変形量がわかれば応力が決まる)のと同様に、流体力学では応力-歪み速度の関係から流体の流速が決まります。構造力学では応力と歪みが線形の関係にある構造体を線形弾性体と言いますが、流体力学でも応力と歪み速度が線形の関係にある流体に名前が付いており、ニュートン流体と言います。
より具体的には、流体に発生する応力は静圧と粘性応力の2つで構成されます。静圧は静止している流体に働く応力です。重力を無視した場合、静止した構造体に応力は発生しませんが、流体の場合は流れが無くても応力が発生します。一方、粘性応力は流体が運動している時に発生する応力を表し、ニュートン流体では歪み速度に比例します。粘性応力は流れを抑制する方向に働き、流体の運動エネルギーは減少します。運動エネルギーの減少分は最終的に熱エネルギーへと変わります。構造体の振動が減衰する過程(材料減衰)と類似の現象と言えるでしょう。
上述のように、流体に発生する静圧や粘性応力は流体の流れに関係します。流れは流速と静圧で記述され、運動方程式と後述の連続の式から求められます。次節ではこれらの式の導出を行います。
流体の支配方程式
流れを記述するとき、流れの中のある特定の部分の流体に着目し、周囲の流体と区別して流体要素と言います。また、無限に小さい流体要素を流体粒子と言います。流体粒子は1つ1つがニュートンの運動方程式に従い、このような粒子が集まって大きな体積の流体が構成されていると考えます。この流体粒子の運動を支配する方程式を立てるにあたって、空間的に固定された座標を使うのか、粒子と共に動く座標系を使うのか決める必要があります。前者の記述法をオイラー記述、後者をラグランジュ記述と言いますが、ラグランジュ記述は流体粒子の間に働く力に依存する瞬間的な速度場を示すことが難しく、理論的な扱いが難解になります。本稿ではより扱いが簡単なオイラー記述で支配方程式を導出します。
図3 微小流体要素を通過する一方向流れ
連続の式
運動方程式の導出に先立ち、質量の保存則を導出します。図3のように空間に固定された体積ΔVの流体要素を考えると、流体要素内の質量は、要素内に入ってくる質量と出て行く質量によって時間変化します。
流体要素内の質量は密度と体積の積よりρΔVと表されますので、微小時間Δtでの質量の変化は
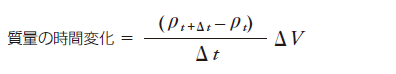
一方、この流体要素に流入/流出する質量は、簡単のためx方向の流速uのみ考えますと、密度、流速、断面積の積より次式で表されます。
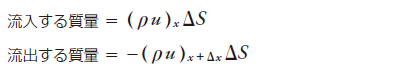
これらの和は質量の時間変化に等しいので、
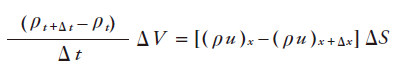
ΔV= ΔxΔyΔz, ΔS=ΔyΔzを代入し、Δt→0 , ΔV→0の極限を取ると、微分の定義より
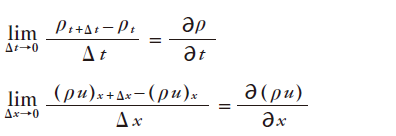
であるため、式を整理すると
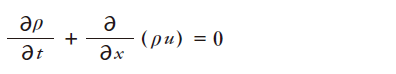
流速がy, z成分を持つ時も同様の議論が成り立つので、v,wをy,z方向の流速として
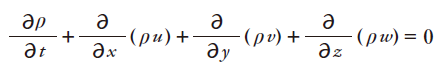
ベクトル形式では
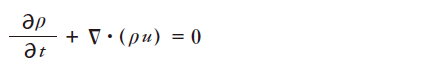
ここでuはu=(u,v,w)で改めてベクトルを表し、∇はナブラ演算子で勾配(gradient)、ドットは内積を表します。この式を質量保存の法則、または連続の式と呼び、質量が保存するように流体が流れることを意味しています。特に、流体が非圧縮性(密度ρ= 一定)の場合は簡単に表すことができ、

運動方程式
連続の式の場合と同様に、まずは図3の流体要素を通過する一方向流れの運動量の保存を考えます。
流体要素内の運動量は密度、体積、流速の積よりρuΔVと表され、微小時間内での運動量変化は
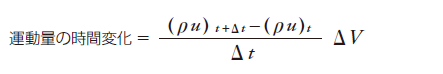
一方、流体要素に流入/流出する運動量は、ρuΔSが単位時間当たりに断面を通過する流体質量なので、さらに流速をかけて
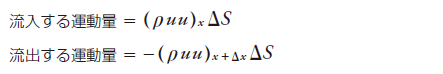
また、流体要素に働く外力Fを加えると、運動量の保存は以下のように表されます。
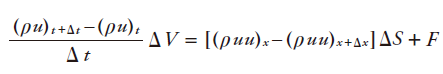
単位体積当たりの外力をfとして、連続の式の場合と同様にΔt→0, ΔV→0の極限を取ると
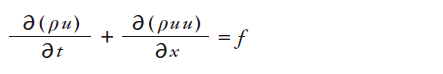
流速がy,z成分を持つ時も同様の議論が成り立つので、
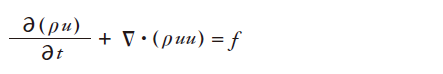
ここでuは改めてベクトルとしています。左辺を展開すると
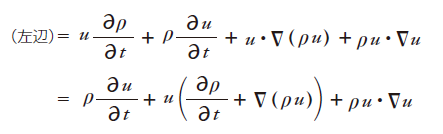
上式の( )内は連続の式にuをかけたものに等しいのでゼロとなり、
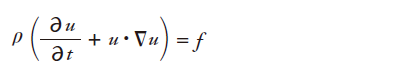
流体要素に働く外力fには、流体要素の面積に比例する力(面積力)と体積に比例する力(体積力)とがあります。前節で触れた静圧と粘性応力は面積力で、方程式中では次式で表されます。
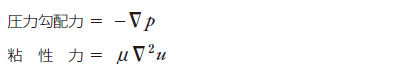
圧力勾配力は静圧pの勾配と逆方向に働きます。つまり、上流から下流に向かって圧力が減少するとき流体は加速され、逆圧力勾配の場合は減速されます。粘性力は非圧縮性を仮定した場合の式ですが、係数μ(ミュー)を粘性係数または粘度(Viscosity)と言います。例として20°Cの空気では1.8×10-5 [Pa s]、水の場合 1.0×10-3[Pa s]の値となり、空気の方が粘性が高く、流体の運動に抵抗する力が大きいと言えます。一方、代表的な体積力としては浮力が挙げられます。浮力については第3回熱流体解析概要で触れます。以上の力を加え、最終的には以下の式が得られます。
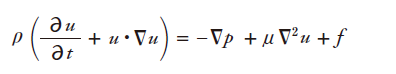
この式を非圧縮性の運動方程式またはナビエ・ストークス方程式(Navier - Stokes equation of motion)と言います。
連続の式と運動方程式は流れを記述するための最も基本的な式で、2つを合わせて流体の支配方程式または基礎方程式と呼びます。非圧縮性流体の場合、流速3成分と静圧の4つの未知変数に対して、連続の式と運動方程式3成分、合わせて4つの方程式が成立するため、これらの方程式から解を求めることができます。一方、密度が変化する流体(圧縮性流体)の場合、密度も未知数となるので、解くべき変数は合わせて5つになります。この場合、新たに密度を解くための方程式が必要となります。例えば理想気体の状態方程式は密度と圧力、温度の関係を表し、圧力と温度から密度を求めることができますが、温度が未知数であるため、温度を解くためにさらに別の方程式(エネルギー方程式)が必要となります。このように、解くべき変数が増えれば、それに応じて必要な方程式の数も増えることになります。
おわりに
今後の連載では、今回導出した支配方程式に基づき、流体解析を掘り下げていきます。次回は方程式から流体力学で最も重要な無次元数の1つであるレイノルズ数を導出し、さらに乱流の基礎についてご紹介する予定です。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

非線形解析の壁を突破するシミュレーション技術
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない実レベルの振動解析
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化する
~薬剤送達効率向上に向けた解析~
-

医薬品バイアルの温度挙動解析
~保管環境の影響把握と品質維持に向けた可視化アプローチ~
-

そのFDTD計算、もっと速くできる!Lumerical+GPUでフォトニクス解析に革命を