CAEを学ぶ
シミュレーションと実験を組み合わせた振動解析入門
はじめに
ものづくり(製品開発の現場)において、試作とテスト(実験)を繰り返す開発から、積極的にシミュレーションを活用し試作とテストを減らし、開発期間やコストを削減しようとする動きが進んでいます。今日では、部品メーカーのレベルにまで広がりをみせ、シミュレーションの需要は、今後も拡大していくと予想されています。それでも、試作やテストがなくなることはありません。シミュレーション結果を検証する実験、解析に必要なデータを得るための実験など、解析が進むほど実験の重要度も高まっています。
シミュレーションの使われ方やシミュレーションへの要求を考えると、2つに分けることができます。1つは実験結果との相関や解析精度を求める場合であり、もう1つは設計判断材料の一部としてシミュレーションを利用するような場合です。前者は、解析専任者が、ハイエンド系CAEツールと呼ばれる高機能なソフトウェアを使用し、ある物理現象をより高精度にシミュレーションすることを追求していくような場合です。後者は、3次元CADを使っている設計者が、CAD環境に統合された視覚的で操作しやすいソフトウェアを使用し、実験との比較や精度というよりは、注目しているパラメータによるシミュレーション結果の違いを相対比較して設計を検討するような場合です。 シミュレーションと実験とは密接な関係にあります。必要な解析結果を得るために、設計者は妥当なパラメータの入力が要求されます。その際、対象物の実データが必要になります。実験担当者と同じレベルになれればそれは素晴らしいことですが、まずは、実験とはどのようなものなのかを体験してみることが重要です。
そこで、振動問題の基礎知識及びモード解析について説明した後、Ansys Workbenchによるモード解析と、実験モード解析(実験で得たデータ(周波数応答関数)を利用した振動モード形の可視化)について紹介します。
振動問題へのアプローチ
「振動」「振動対策」というと何か難しいもののように思われがちですが、意外に身近なところで使われています。
例えば、スポーツ分野では、テニスラケットやゴルフクラブの設計に振動解析が利用されています。家電製品では、洗濯機の振動や音対策、冷蔵庫やエアコンの静音化が進んでいます。自動車であれば、車としての機能・性能に加え、乗り心地などの快適性を高めるために振動や音が密接に関わっています。
また、振動と騒音は全く別のものであると思われがちですが、クレームなどの原因は騒音という形で現れ、結果として振動対策を施して問題が解決することも少なくありません。
振動問題では、実験とシミュレーション共に必要とされています。振動対策を考えるためには、振動問題についての基礎的な知識を背景に、理論解析及び実験解析の両方からのアプローチが有効かつ必要なためです。
振動解析の1つの手法にモード解析という方法があります。詳細は後述しますが、有限要素解析(FEM)ソフトによる理論モード解析と、実験データから解析する実験モード解析とがあります。一般に、モード解析と言った場合には、実験モード解析のことを意味します。
振動問題の基礎知識
振動問題では、固有値(固有振動数)、減衰、固有モードの3つが重要です。
固有値(固有振動数)が明らかになると、対象となる構造物が、どの周波数(何Hz)で振動しやすいかが分かります。減衰からは、どれだけ振動が持続するか、あるいは、どれだけ振動がおさまりやすいかが分かります。固有モードからは、構造物がどのような形で振動するかが分かります。
3.1 固有値(固有振動数)
固有振動数とは、図1に示す周波数応答関数(伝達関数)のピークの位置になります。固有振動数は、その構造物固有のもので、同図の1次モードの場合、1次の固有振動数である203Hz近傍で加振すると、対象物が激しく振動(共振)し、場合によっては対象物が壊れてしまうこともあります。このような場合、対象物の構造を変更して剛性を上げる(構造的に強くする)対策などが行われています。
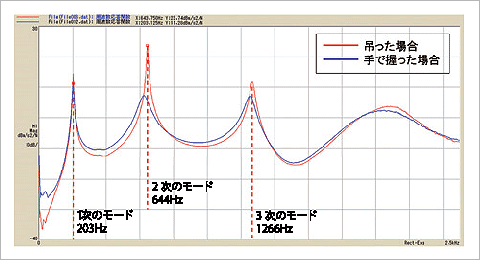
図1 バットの周波数応答関数の比較(横軸:周波数、縦軸:アクセレランス)
3.2 減衰
減衰は、図1に示す周波数応答関数のピークの鋭さ(あるいは鈍さ)です。ピークが鋭いほど減衰が小さいことを示し、構造物自体が振動しやすい、発生した振動が持続しやすくなります。同図において、赤線はバットを吊った状態、青線はバットを握って加振した場合です。バットを手で握ることにより、減衰が加わり各モードの共振周波数におけるピークが鈍くなっています。
減衰が大きいと共振周波数近傍でもあまり大きな振動問題にならない場合があります。また、減衰は実験的に求められることが多く、実験モード解析が有効です。減衰の計測、評価は非常に難しく、誤差が大きいのが現状です。
3.3 固有モード
一般に構造物は連続体(分布定数系)であり、無限のモードを持ちます。ある固有値における振動は、決まった形をしています。これを固有モードといいます。固有モードは、周波数の低い方から1次モード、2次モード・・・と呼びます。固有モードが分かると、振動の形状をイメージしやすくなるため、振動対策の検討がしやすくなります。 振動を止めるには振動の大きいところ(よく動くところ。振動モードの腹。図2の赤い部分。)を選んで対策します。振動を伝わりにくくしたい場合には、振動が少ないところ(動きにくいところ。振動モードの節。図2の青い部分。)を選びます。
モード解析とは
モード解析を理論的に説明すると、「物理座標系からの座標変換により、モード座標系と呼ばれる直交座標系で振動系を解析する手段であり、数学的には一般固有値分解に基礎をおく」となります。もう少し分かりやすく説明すると、固有値解析という手法を使い、図3に示すように連成した物理座標系の多自由度系力学モデルを、非連成化した複数の1自由度系力学モデルに変換する方法です。これにより、複数のモードを独立した1つのモードに分離できるため、モデルの取り扱いが容易になります。
有限要素解析(FEM)による理論モード解析、実験モード解析共に、最終的にモード解析アニメーションを作成できる点は同じです。しかし、図4に示すように、両者は全く別のアプローチをとります。前者がAnsysなどのFEMツールで行う振動解析であり、後者は加振実験により取得した周波数応答関数に対しカーブフィットと呼ばれる処理を行い、振動特性を同定します。
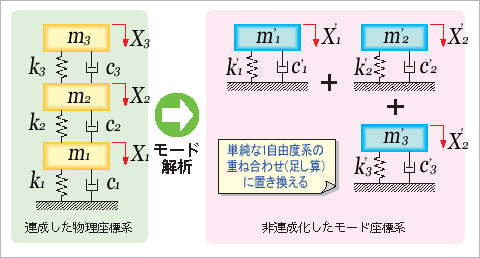
図3 モード解析のイメージ
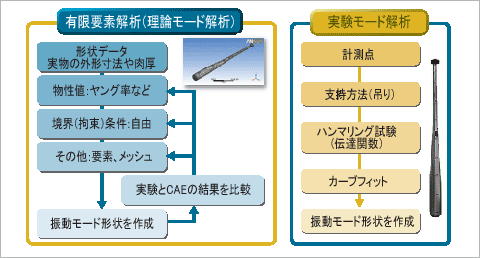
図4 振動モード形状を求める手順の比較
バットの振動解析
解析(実験)をするためには何のために解析(実験)するのかという目的を明確にすることが重要です。ここでは、ホームランを振動という面から説明することを目的にします。 まず、ホームランという現象に対し仮説を設定し、Ansys Workbenchによる理論モード解析、実験モード解析(周波数応答関数のデータを使った可視化)を行います。
5.1 仮説
まず、「ホームランとは、打球をもっとも遠くに飛ばすこと」と仮定します。
ここで、ホームランに限らずバッティングをした時の経験を思い出してください。経験の中に本質的な答えやヒント(きっかけ)が隠れていることが多いからです。
例えば、「ホームランを打った場合には、打った感触がない。」、「スイートスポットというのがあるらしい。」といった話を、振動を切り口に考え直します。すると、「バットが振動していないということではないのか?」、「打撃ポイントがバットの節になっているのでは?」といった予想が立てられます。「ボテボテの内野ゴロをうったような場合には、手がビリビリしびれた。」ことを同様に見直してみると、「打撃がバットへの加振になっているのかも?」、「しびれるのは高い周波数のような気がする?」などと考えられます。 このような思考過程においては、物事を客観的に見て、できるだけシンプルに分解していくことが大切です。
ホームランのプロセスについて考える場合も同様にシンプルに考えていきます。投球については、「打撃ポイントにボールが静止している。」と仮定します。バッティングについては、「バットは水平方向に移動する。」と仮定します。打球の飛翔経路については、「どのような経路で飛翔するのが最も少ないエネルギーで遠くに飛ぶのか?」といったことも考えられますが、今回の解析目的からは外れるのでここでは省略します。
以上の考察内容を整理すると、「スイングにより発生した運動エネルギーを、最大限ボールに伝えるにはどうすればよいのか?」、「バットには固有振動数があり、固有モードがある。」となり、次の仮説が立てられます。
「バットが共振しないように打撃できれば、バットの運動エネルギーを最大限ボールに伝えることができ、ホームランになるのではないか?」 この仮説を検証するために、モード解析を使い、振動モード形状により考察します。Ansys Workbenchによる理論モード解析と、実験モード解析により、理論と実験の両面から解析を進めます。
5.2 Ansys Workbenchによる理論モード解析(FEM)
まず、バットの形状モデルを読み込み、メッシュを作成します。図5に示したバットのメッシュは、15743節点、7827要素です。次節で説明する実験モード解析と比較すると、実験モード解析は計測箇所が9点、自由度も1自由度であるのに対し、FEMでは1点当たり6自由度(並進3、回転3)あります。この自由度のように、シミュレーションをするためにも、実験の制約を知っていると解析結果の理解を深めるために役立ちます。
FEM解析の場合、対象物の形状データからメッシュを作成します。従来は、このメッシュを作る機能が解析作業全体に占める割合が大きく、オートメッシュできれいなメッシュを得られなかった場合の修正作業に時間がかかっていましたが、最近では修正作業を含め効率よくメッシュを作成することができるようになっています。

図5 Ansys Workbenchで作成したバットのメッシュ表示例
次に、Ansys Workbenchにより理論モード解析を行います。図6に、解析画面の1例を示します。シミュレーションウィザードを使うことにより、もれなく確実な解析設定及び解析が行えます。ここでは、20個の固有モードを計算しています。拘束条件をフリーとしているため、1次~6次モードは、剛体モードです。7次、8次モードが、実験モード解析の1次モードに対応します。
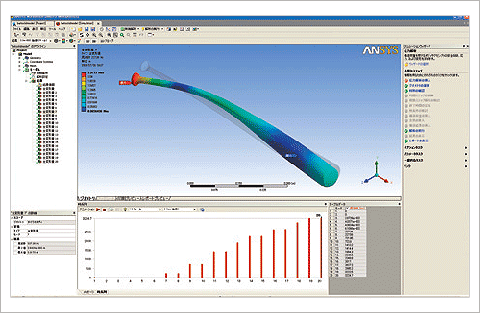
図6 解析画面例
5.3 実験モード解析(周波数応答関数のデータを使った可視化)
実験モード解析ソフトも専用のものが市販されていますが、ここではFFTアナライザで計測した周波数応答関数データから、固有振動数における大きさ(アクセレランス)と位相の情報を利用して、振動モード形状を作成する方法を紹介します。なお、ここでは、カーブフィットは行っていません。

図7 弊社2008年度新人技術
研修における1コマ
(2)計測データの可視化 計測したデータ(周波数応答関数)を使い、振動モード形状を作成します。ここで使用したデータは、1次から3次までの固有振動数におけるアクセレランスの値と位相の符号情報のみです。図8に、計測画面例を示します。
振動モード形状の作図そのものは、手書きでも表計算ソフトを使っても可能です。ここでは、作図した振動モード形状をアニメーションさせるために、数式処理ツール Maple 12を使っています。作図例を図9、10に示します。
5.4 考察
理論モード解析及び実験モード解析の結果から、以下のように考えられます。
(1)「ホームランは打った感触がしない。」のは、スイートスポットが各モードの節に近いため、バット自身が振動しにくいためと考えられます。
(2)「バットの根元付近で打つと手がしびれる。」のは、バットの根元(細くなっている当たり)は、各モードの腹に近いため振動しやすいためと考えられます。
(3)以上の結果をふまえ、バットを握った場合等、より実際の現象に近い条件での解析に進むことができます。
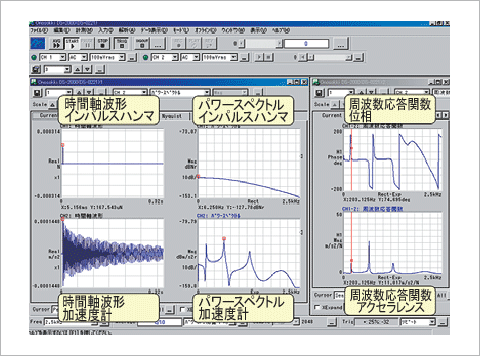
図8 計測画面の1例
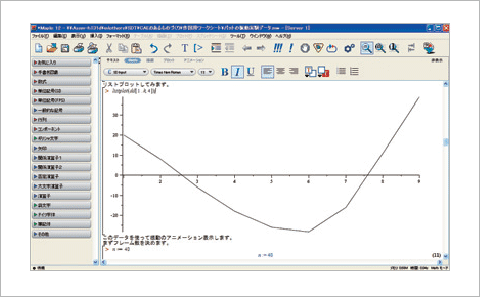
図9 Maple12による振動モード形状の作成例
図10 Maple12による振動モードアニメーション表示例
おわりに
ホームランとバットの振動解析をテーマに、Ansys Workbenchによる理論モード解析と、実験モード解析の両面から振動問題を扱う手順について説明しました。実際のものづくりにおいては、このようなシンプルな解析では解決できないような場合も多々あるのでしょうが、まずは、基礎的な事例について経験を積むことで、振動問題の知識を身につけた技術者が育ち増えることにより、日々振動対策に追われ忙しく飛び回っている方への助けになることを願っています。
【実験モード解析の参考書】「モード解析入門」 長松昭男 著 コロナ社
(CAEのあるものづくり2008年9号掲載)