データの次元数
Field ファイル作成で迷う所の一つに“データの次元数”があると思います。
データの次元数には「(A) データ構造の次元数」 と 「(B) 座標値の次元数」 があります。
以下では具体例を示しながら、(A) (B) の違いを説明します。
例 1
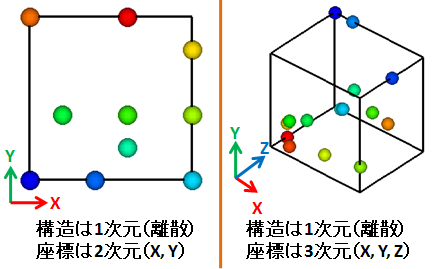
例えば、“データポイントが空間上のあちこちに分布している”データ。
よくあると思いますが、こういった“離散点の集まり”の場合、
(A) は 1 次元 (支援ツールでは「離散型」となっています) です。
“構造”としては「データポイントの定義の順番」のみなので、1次元とみなします。
(B) は 2 次元か 3 次元のどちらかになります(データポイントが分布する空間の範囲による)。
具体的には、ポイントがすべて同一平面上にあれば(座標値が X, Y だけなら) 2 次元、そうでなければ(座標値が X, Y, Z なら) 3 次元です。
下図の左は (B) が 2 次元、右は (B) が 3 次元の離散点データです
(枠線は分布空間を表す便宜上のものです)
(B) が 1次元である(座標が X のみで、データポイントが一直線にならんでいる)ことは 稀だと思います。
例 2
碁盤の目のような 2次元的な構造格子があったとして、それが平面で直交するのではなく、 3 次元空間に湾曲して存在する場合、例えば下図のような場合は

(A) は 2 次元 となります。マス目が歪んではいますが、
構造上は、「何行目の何列目」で各格子点が特定できるからです。
(B) は 3 次元 となります。各格子点の座標値は X, Y, Z の
3次元で定義する必要があります。
上記の【例 1】【例 2】は (A) と (B) の次元が異なる代表的な例ですが、こういったデータは実際に扱われる事は多いと思います。
Field ファイルのアスキーヘッダー (*.fld) にはいくつかのキーワードがありますが、上記の(A) は キーワード ndim、(B) は キーワード nspace にあたります。
また、(A) を「計算空間の次元」(B) を「物理空間の次元」と呼ぶこともあります。
まとめ
(A) - ndim - 計算空間の次元 →「データ構造の次元」
(B) - nspace - 物理空間の次元 →「座標値の次元」