CAEを学ぶ
はじめてみよう!流体解析(入門編)[Ⅲ]
~熱流体解析の概要~
はじめに
流れに加えて温度分布も確認したい場合、流れの基礎方程式(連続の式、運動方程式)に加えエネルギー方程式を考慮する必要があります。エネルギー方程式は流体の圧縮性(密度の圧力依存性)の考慮 ※ の有無により理論的な扱いが異なりますが、圧縮性を考慮しなければならないケースが限定されること、及び理論的な扱いがより簡単なことから、本稿では非圧縮性と仮定して説明します。
※ 一般にマッハ数(流速と音速の比)が0.3以上の流れでは、圧縮性の影響が無視できません。
熱の考慮
構造解析で熱応力解析を行う場合、よく伝熱解析との連成解析が行われますが、流体解析においても同様に伝熱解析(エネルギー方程式)と流体解析(流れの基礎方程式)の連成解析がよく行われます。以下に非圧縮性の基礎方程式(1)、(2)とエネルギー方程式(3)を示します。
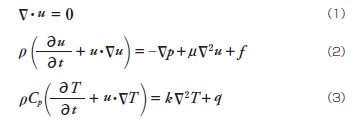
ここでT:温度、Cp:定圧比熱、k :熱伝導率、q :生成(発熱または吸熱)項です。(3)式の左辺第2項(移流項)に流速が含まれており、(1)~(3)式が連立方程式になっていることがわかります。なお、Ansys FluentやAnsys CFXなどのCFDツールでは、固体を含む熱流体解析(共役熱伝導解析;Conjugate Heat Transfer)を行うことが可能ですが、固体領域では流れを考慮しないため、(3)式の左辺第2項が省略され、熱伝導方程式になります。この場合、流体-固体境界面において熱の授受が考慮されます。
浮力
一般に周囲の流体より温度の高い流体は比重が小さくなり、温度の低い流体は比重が大きくなります。そのため重力場において流体に温度差が発生すると次式で表される浮力が発生します。
![]()
ここでΔρ:密度差、g :重力加速度で、(2)式の外力項f に相当します。Δρ> 0 のとき周囲の流体よりも比重が大きいため下降する方向に浮力が働き( f < 0)、Δρ> 0 のとき上昇する方向に浮力が働きます( f > 0)。
このように浮力を考慮する場合には、密度ρが未知数となり、流速三成分(u, v , w)と圧力p 、温度T と合わせて未知数の数は6つとなります。これに対して方程式の数は(1)~(3)式((2)式は流速三成分で3つの方程式)で5つとなりますが、未知数の数より1つ少ないため連立方程式が閉じず、解を得るためには密度と温度の関係を追加する必要があります。
これは熱流体解析を行う場合に、密度の温度依存性に関する追加の設定が必要であることを意味します。代表的な設定を以下に紹介します。
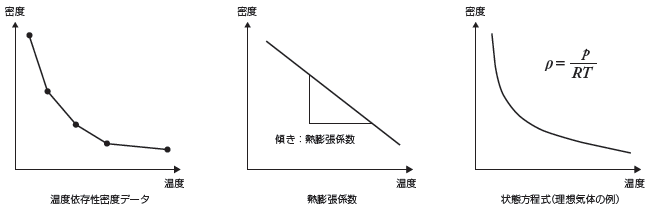
密度 vs. 温度データテーブル
実験や文献などから得られた離散データを入力します。
熱膨張係数(体膨張係数)
密度の温度変化を線形と仮定し、密度変化を以下のように近似します。
![]()
ここでαは1[K]当たりの密度変化率を表す物性値で、熱膨張係数または体膨張係数と呼ばれ、以下の式で定義されます。
![]()
詳細は割愛しますが、(5)式はブシネスク近似(Boussinesq Approximation)に基づいており、扱いが簡単になる一方、密度の温度依存性を線形化しているため他の手法と比較して温度の適用範囲が狭いことが特徴です。
状態方程式
密度の温度依存性をρ= f (T )という関数で表します。例えば理想気体の状態方程式では、ρ= p / RT( p:圧力、R:気体定数、T:絶対温度)という関数で表され、密度が温度に対して反比例します。
これらの手法を模式的に表すと図1のようになります。
強制対流と自然対流
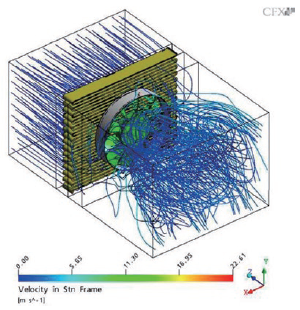
重力場において流体に温度差が形成されれば、浮力は多かれ少なかれ流体の流れに影響を与えますが、解析において常に考慮する必要はありません。例えばファンを駆動力とする流れにおいては、ファンが流体に与える慣性力と比較して浮力は無視できるほど小さく、考慮しないことがよくあります(その分計算負荷も小さくなります)。このような流れを強制対流(Forced Convection)と呼びます(図2)。
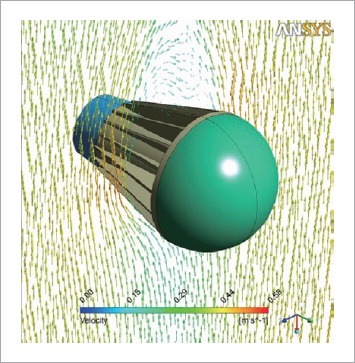
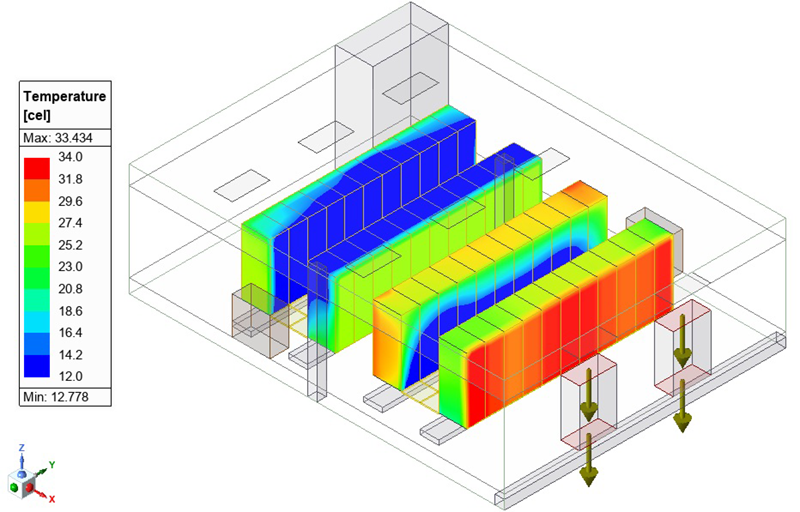
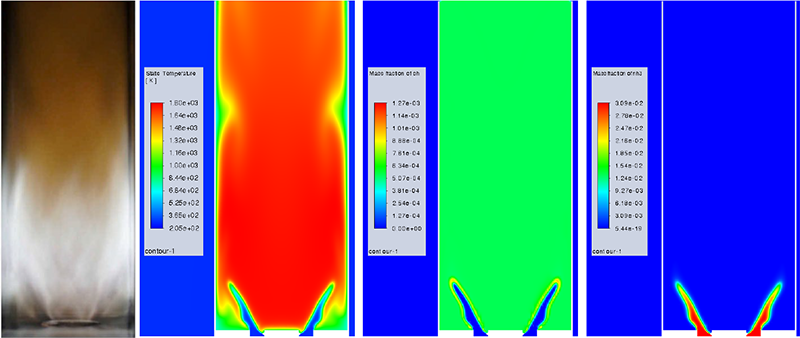
一方、ファンなどの流れの駆動源が無く、静止流体中に設置された発熱体の周囲では、ある程度の時間を置くと浮力による対流が卓越します。このような流れを自然対流(Natural Convection)または自由対流(Free Convection)と呼びます(図3)。
また、解析対象によっては両者が共存し、明確に区別できない場合があります。このような場合、混合対流(Mixed Convection)と呼びます。自然対流と混合対流では浮力の影響が共に無視できないため、解析において3節で説明した密度の温度依存性に加え、浮力の設定も必須となります。ここでは、強制対流と自然対流についてもう少し掘り下げて解説します。
強制対流
既に概要を述べたとおり、外力により強制的に発生させた流れにおいては浮力の影響を無視することが可能ですが、具体的にどんな場合に浮力を無視して良いのでしょうか。
方程式を見てみますと、(2)式の左辺第2項が流れの慣性力、右辺第3項が浮力を表し、それぞれの大きさを見積ると以下のようになります。
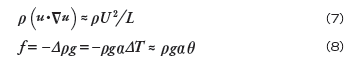
ここで、U:流れの代表速さスケール、L:代表長さスケール、θ:温度差スケールを表し、浮力については(5)式を使用しています。慣性力に対して浮力が無視できるほど小さい場合、(7)式 >>(8)式なので
![]()
という関係式が成り立ちます。温度差スケールの大きさによりますが、浮力によって発生する流れの速度は数mm/s ~数10cm/s程度であることが多く、ファンなどによりこれと比べてとても大きい流速を発生させている場合は浮力の影響は無視できる、と考えて良いでしょう。
(9)式が成り立つとき、(2)式において浮力項はゼロとなります。その結果、強制対流における方程式系では、流れ場((1)、(2)式)が温度場((3)式)に影響を与えますが、温度場は流れ場に影響を与えません。つまり、流体から伝熱への片方向連成解析となります。これは、次に述べる自然対流と比べて強制対流の方が解析の難易度、計算負荷が低い、ということを意味します。
自然対流
外力による流れが小さい、または外力がない場合、浮力の影響を無視することができません。浮力((4)式)の大きさは密度の変化、すなわち温度分布が未知の場合不明であるため、まずはエネルギー方程式による温度場の計算を行わなければなりません。浮力が求まると、連続の式((1)式)と運動方程式((2)式)から速度が求まります。速度はエネルギー方程式((3)式)の左辺第2項(移流項)を通じて温度場に影響を与えます。その結果浮力の大きさが変化し…というサイクルで流れ場、温度場が変化していきます。すなわち、流れ場は浮力を通して温度場に支配される一方、温度場は熱の移流を通して流れ場に依存します。このように、自然対流では流れ場と温度場の相互作用が強いため、流体と伝熱の双方向連成解析になります。その結果、浮力の影響が大きい流れにおいては非常に複雑な流れが発生し、解析の難易度や計算負荷も相対的に高くなります。
相似性
熱流体解析の場合にも、 第2回 で述べた流れの相似性について考えることで、解析に先立ち有益な情報が得られます。流れのみの解析では、幾何学的に相似な状況において、レイノルズ数が等しい場合に相似な流れが発生します(力学的相似性)。しかし、熱を考慮した場合は幾何学的な条件に加えて必要な条件がさらに追加されます。レイノルズ数と同様に無次元数を導入することで相似性について議論されますが、ここでは詳細については割愛し、結論だけ述べます。
強制対流の場合に相似性が成り立つには、レイノルズ数に加えて次式で定義されるプラントル数Pr(Prandtl Number)が等しくなる必要があります。
![]()
ここで、ν(=μ / ρ):動粘性率、κ (= k /ρCp) :熱拡散率(または温度伝導率)で共に物性値です。そのためPr は使用する流体にのみ依存し、特定の流れには依存しません。この条件が追加されることにより、ある条件の強制対流の解析で得られた結果を別の条件の解析に役立てるには制限がつくことになります。
自然対流の場合、浮力が未知のため浮力によって発生する流れの代表速さスケールを解析条件から見積ることができません。その代わり、温度差スケールθを用いて以下の無次元数が定義されます。
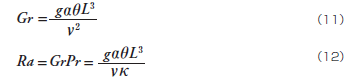
(11)式をグラスホフ数Gr(Grashof Number)、(12)式をレイリー数Ra(Rayleigh Number)と呼びます。Gr、Raは定義が異なるものの共に対流の強さを表す無次元数ですが、Pr は特に水平層の対流について使用されます。自然対流ではPr((10)式)と合わせた3つの無次元数のうち、2つが等しければ相似性が成立する、と言うことができます。
いずれの場合も2つの無次元パラメータによって流れが支配されるため、単一のパラメータ(レイノルズ数)で支配される流れのみの場合と比較して相似性が成り立ちにくいと言えるでしょう。
おわりに
熱流体解析と言うと、市販されているCFDツールのほとんどのカタログで筆頭の機能として記載されており、入門レベルの流体解析というイメージがあります。確かに、圧縮性流れや多相流、燃焼流などに比べると物理モデルは比較的簡単で、計算負荷は小さく、解析難易度も低い部類と言えます。しかし、特に自然対流においては、浮力を考慮するだけでありながらも実験事実として非常に複雑で多様な様相を見せる現象であることが知られています。解析においても収束させることが困難になりがちで、必要とする精度によっては計算が長時間に及ぶことも少なくありません。第2回にご紹介した乱流モデルとともに、解析に先立ってどれくらいの精度が必要なのか検討する必要があります。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~