CAEを学ぶ
はじめてみよう!流体解析(入門編)[Ⅱ]
~レイノルズ数と乱流~
はじめに
乱流は工学設計において性能を損なう要因になる一方、性能を向上させる要因にもなります。例えば、流線型物体 ※1に作用する抗力の増大、構造物の振動、乱流騒音など設計上好ましくない現象の発生要因となる一方で、熱交換器の冷却効率の向上や物質の混合を促進させる要因にもなります。このように乱流は様々な問題に関連し、適切な設計を行うためには乱流現象を理解し、それぞれの問題にどのような影響を及ぼしているのかを把握する必要があります。そのために、従来では実験が行なわれてきましたが、近年ではCFDによるアプローチも取られています。
そこで今回はCFDで乱流の解析を行う際に必要な知識として、乱流に関わる重要な無次元数であるレイノルズ数、さらに乱流の特徴と乱流モデルについて取り上げます。
レイノルズ数
レイノルズ数は、オズボーン・レイノルズ(Osborne Reynolds 1842~1912)が導入した無次元数で、次式で定義されます。

ここでρは密度、μは粘性率、Uは代表流速、Lは代表長さ(代表寸法)です。代表流速と代表長さは流れを特徴づける値を選びます。例えば円管内の流れにおいては流入流速をU、円管の直径をLに取ることが一般的です。レイノルズ数はこのように、流体の物性( ρ,μ)と解析条件( U,L)が決まれば計算することができ、事前に流れのパターン(層流、乱流)の見当をつけるために使用されます。
レイノルズ数の導出
まずはレイノルズ数の導出を行います。前回導出した非圧縮性の連続の式と、x方向の運動方程式を直行座標系で以下に示します
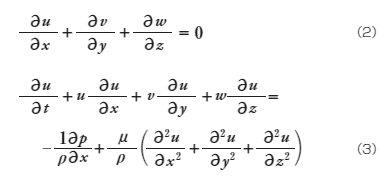
(3)式の左辺第2項~第4項は慣性項または移流項と呼ばれ、流速の2次に比例していることから非線形項とも呼ばれます。この非線形性のため流体の運動方程式の厳密解を求めることができるのはごく一部のケースに限られ、流れの研究は理論と実験の両方のアプローチが取られてきました。
実験では模型実験がよく行われます。実物を用意することができない場合や、用意するのにコストがかかる場合、実物を縮小した幾何学的に相似な形状の模型を用意します。形状が相似であることを流体力学では特に幾何学的相似性と呼び、以下のように表します。
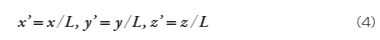
ここで、 x, y,zは実物の各軸方向の寸法、 x’, y’, z’は模型の寸法、Lは両者の比で無次元の長さを表します。では、幾何学的相似性を満たせば実物と同じ流れが再現されるのでしょうか ―答えはノーです。例えば、対気速度 200 m/s(時速 720 km/h に相当)で飛行する航空機を考える場合、幾何学的に相似な模型に 200m/s の風を当てても実物と同じ流れは再現されません。模型を 200m/s で飛ばしても同様です。
それでは、どのような条件で模型実験を行えば良いのでしょうか。結論を先に言うと、レイノルズ数が同一である必要があり、これを力学的相似性と呼びます。幾何学的相似性に加えて力学的相似性が満たされれば同じ流れのパターンが再現されます。この条件を導くため、流速の相似性を考えます。幾何学的相似性と同様にして、
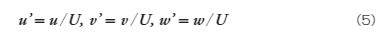
u, v, wは実物の各軸方向の流速、 u’, v’, w’は模型の流速、 Uは両者の比で無次元の流速を表します。(4)、(5)式より時間、圧力に関しても相似性を考えることができ、
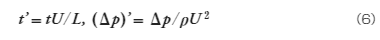
基礎方程式(2), (3)式に(4)~ (6)式を代入し、模型の流れを記述する方程式に変換すると
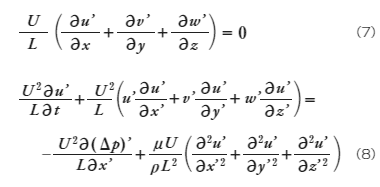
さらに式を整理すると以下の式が得られます。
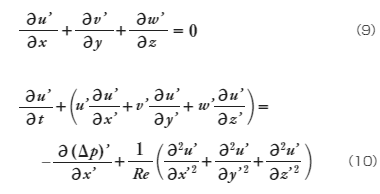
ここで(10)式のReは(1)式で定義されているレイノルズ数です。得られた方程式を見ると、連続の式(9)は元の式(2)と同一の形をしています。運動方程式(10)はレイノルズ数だけがパラメータになっており、幾何学的相似性を満たす2つの流れにおいてレイノルズ数が同じであれば同じ方程式によって流れは記述され、同じ流れのパターンが得られることがわかります。
レイノルズ数の利点
レイノルズ数(以下、Re)を考えることにより、模型実験を行うとき、模型実験のReと実物のReを同一にすれば同じ流れのパターンが得られることがわかりました。これは、Reさえ同じ値にすれば、模型実験の流体(物性値)、代表流速、代表長さを自由に変更して良いことを意味し、実験方法の選択肢が広がります。
また、解析を行うにあたっては、幾何学的に相似な解析モデルにおいて、Reが同じ実験結果または解析結果が過去に得られていれば、新しい解析を行う前に流れのパターンをある程度予想することができます。特に収束性などのトラブルが発生しやすい解析では、過去の経験を生かすことで作業の効率化が期待できます。

図1 層流 Re = 1.54 [1]
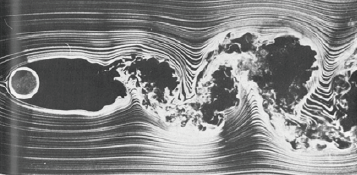
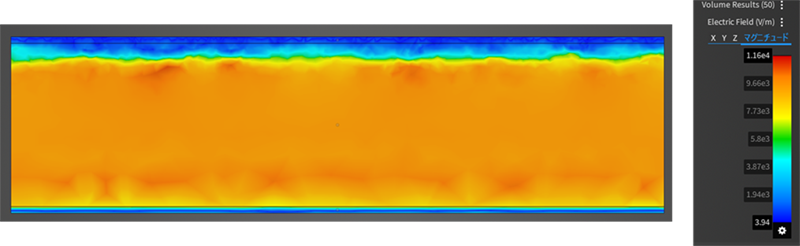
図2 乱流 Re = 10,000 [1]
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

実測 × 解析で基板の熱変形問題を解決!基板反り現象の高精度シミュレーション
~エスペック(株)×サイバネットシステム(株)の連携ソリューション~
-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~