資料ダウンロード
人間の皮膚および光学心拍センサーのモデリング

解析概要
近年広く普及しているスマートウォッチでは、内蔵されている心拍センサーによって脈拍を測ることができ、自身の健康状態をいつでも手軽に確認できるようになっています。この心拍センサーに利用されているのが、光電式容積脈波記録法(以下、PPG:photoplethysmography)と呼ばれる光学技術です。PPGは、皮膚に光を照射し、血流に伴う血液量の変化を検出する非侵襲な計測手法であり、脈拍や血中酸素飽和度(SpO₂)などを測定する目的で、さまざまなヘルスケア機器に応用されています。
本稿では、参考文献を基に、光学設計ソフトウェア Ansys Zemax OpticStudio(以下、OpticStudio)のノンシーケンシャルモードで、人間の皮膚と血液をモデリングし、PPGの時間依存シミュレーションをPythonとのAPI接続にて実行する方法をご紹介します。
背景/課題
非侵襲計測技術
体を傷つけることなく体内の状態を検査する非侵襲計測技術は、被験者への負担が小さく、安全かつ手軽に実施できることから、今後さらに普及していくことが期待されています。その中核技術の一つとして活用されているのが光です。検査対象に光を照射し、組織内で散乱・反射した光を検出・解析することで、人体の状態を間接的に評価することができます。
一方で、非侵襲計測では対象を直接観察・測定できないため、得られる情報の信頼性を確保するには高い測定精度が求められます。そのため、実環境を忠実に再現したシミュレーションによる評価や検証が重要となり、測定環境を高精度で再現することが不可欠となります。
PPGセンサー
血液を対象とした光学計測では、主に可視光および赤外光の波長帯が利用されます。光の波長によって皮膚や組織内への到達深さや吸収特性が異なるため、測定対象や目的に応じた波長の選定が重要となります。
例えば、血中酸素濃度(酸素飽和度:SpO₂)のような血液成分の評価では、皮膚の深部まで到達しやすい赤色光や近赤外光を用い、ヘモグロビンの吸収特性の違いを利用して測定が行われます。一方、本稿で取り扱うPPGによる脈拍解析では、ヘモグロビンによる吸収が大きく、皮膚浅層の血液量変化を高感度に捉えられる緑色や黄色の波長が適しています。これらの波長では、血液量変動に伴う光吸収の変化が顕著に表れるため、PPG信号を明瞭に観測することができます。
このように、PPGにおいては波長選定に加えて、光をどのように生体に照射し、検出するかというセンサー構成も測定性能に大きく影響します。PPGには、反射型と透過型の二つの検出方式があり、発光部と受光部が生体の同一側に配置されているものが反射型、生体を挟んで対向して配置されているものが透過型です。これらの方式は、計測対象や目的に応じて使い分けられます。
反射型PPGは、脈拍測定のような血流の変化を捉える用途に適しており、スマートウォッチなどのウェアラブル機器で広く用いられています。一方、透過型PPGは血中酸素飽和度などの血中成分分析に適しており、指先に装着するパルスオキシメーターに採用されています。本稿では、反射型PPGセンサーを対象として検証を行います。
設計の仕様
光源とセンサー
本解析では反射型PPGの光源として、皮膚および血液の光学パラメータが広く報告されている波長を対象とし、モデル化を行いました。具体的には、波長575nmを採用し、光源にはQSMF-C160 LED(Avago Technologies社製)を用いています。スマートウォッチでの利用を想定し、光源は人体モデルの表面側に配置しています。
センサーは光源と同一側に配置し、受光部は2mm × 2mmの領域を持つ1ピクセルの検出器としました。本解析では、PPGセンサーに入射する照度を取得することを目的としており、空間的な照度の分布は評価対象としていません。そのため、検出器は1ピクセルのみの構成としています。
皮膚と血液のモデリング
本解析では、PPGセンサーによる脈動の観測に着目するため、血液が流れる真皮を詳細にモデリングします。具体的には、乳頭層、上部毛細血管網層、網状層、下部毛細血管網層の4層構造を対象とします。一方、真皮の上に位置する表皮には血液が存在しないため、モデルを簡素化する目的で、角質層、顆粒層、有棘細胞層、基底細胞層をまとめて一つの厚い表皮層として仮定します。
各皮膚層内の血管構造を幾何学的に正確にモデリングする場合、構造が極めて複雑になり、解析に必要な要素数も膨大になります。そのため、本解析では血管構造を簡略化して再現します。具体的には、血液をジオメトリとして明示的にモデリングするのではなく、光線の伝搬挙動の変化として表現するため、屈折率によって血液の存在を再現する手法を採用します。
以上を踏まえ、参考文献に基づいて、本稿での解析に用いる皮膚の層構造および光学パラメータを、表1に上層から下層の順でまとめます。最下行には血液の光学パラメータを記載しています。図1ではOpticStudioで皮膚の層構造をオブジェクトで再現した様子を示しています。OpticStudioでは、皮膚を矩形体積オブジェクトとして表現し、血液は独立したオブジェクトとしてはモデル化しません。その代わりに、各皮膚層の材質として設定する屈折率により、血液の影響を反映させています。
具体的には、皮膚そのものが持つ屈折率、血液の屈折率、ならびに皮膚層内における血液量を考慮し、脈拍に伴って微小に変化すると想定される各皮膚層の屈折率を算出し、光線追跡の際にその屈折率を各皮膚構造に再定義します。
なお、これらの設定は人体の皮膚構造を一意に定義するものではありません。実際には個人差が存在するため、本モデルは平均的な特性を仮定した近似モデルである点に注意が必要です。
| 構造 | 厚み[mm] | 屈折率@ 575nm | 層内の血液量[%] |
| 表皮 | 0.1 | 1.450 | 0 |
| 乳頭層 | 0.15 | 1.399 | 2 |
| 上部毛細血管網層 | 0.1 | 1.398 | 5 |
| 網上層 | 1.5 | 1.400 | 1 |
| 下部毛細血管網層 | 0.1 | 1.398 | 5 |
| 皮下脂肪 | 6.0 | 1.436 | 5 |
| 血液 | - | 1.35 | - |
表1 : 人体のモデリングのための各種パラメータ
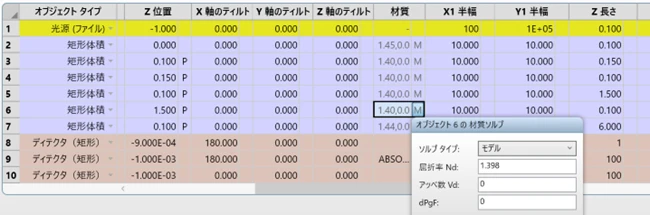
図1 : 皮膚のモデリング
さらに、光が人体の中で発生させるバルク散乱も定義します。生体組織などの混濁媒質内の微粒子による散乱は、Henyey-Greenstein分布関数で再現できます。この散乱光の角度分布は下記式で求められます。
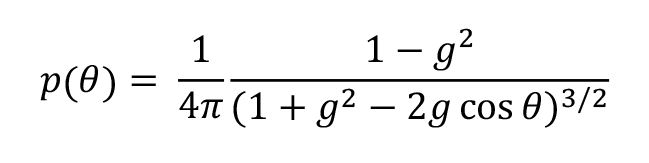
この関数の自由パラメータは、異方性パラメータ gのみです。gの領域は-1~1の範囲にあり、g= -1 は後方散乱、g= 0 は等方性散乱、g= 1 は前方散乱に対応します。
OpticStudioではHenyey-Greenstein散乱DLLで散乱を再現します。この際、参考文献に発表されている現実的な値に基づいて各層の散乱パラメータを設定しています。散乱の入力パラメータは平均光路(Mean Path)、透過率(Transmission)、異方性パラメータgです。一方、参考文献では一般的に、異方性パラメータとともに散乱係数μsと吸収係数μaが掲載されています。このため、モデルの入力パラメータである平均光路と透過率を、散乱係数μsと吸収係数μaで次式のように計算しました。
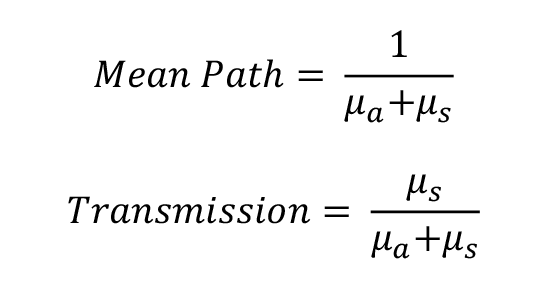
以上から、表2に各皮膚層について、今回使用する波長575nmにおける散乱係数、吸収係数、そこから求められる平均光路とTransmission、異方性の各パラメータをまとめます。
| 構造 | μa[1/mm] | μs[1/mm] | 平均光路 | Transmission | g |
| 表皮 | 1 | 20 | 0.0476 | 0.9524 | 0.79 |
| 乳頭層 | 0.28 | 21.5 | 0.0435 | 0.9599 | 0.79 |
| 上部毛細血管網層 | 0.28 | 21.5 | 0.0403 | 0.924 | 0.79 |
| 網上層 | 0.28 | 21.5 | 0.0447 | 0.9731 | 0.79 |
| 下部毛細血管網層 | 0.28 | 21.5 | 0.0403 | 0.924 | 0.79 |
| 皮下脂肪 | 0.081 | 1.396 | 0.1811 | 0.6928 | 0.75 |
| 血液 | 32.4 | 50 | - | - | 0.98 |
表2 : 人体のモデリングに対する散乱パラメータ
図2はOpticStudioでHenyey-Greenstein散乱を設定する実際の画面です。表皮に対する設定画面を示しています。
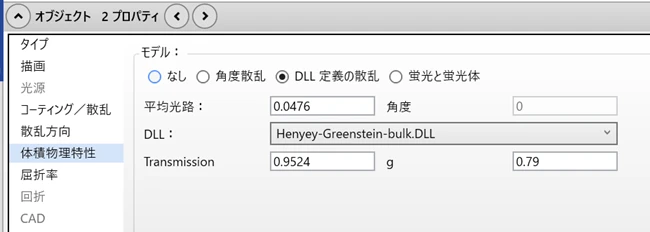
図2 : 散乱の設定(表皮の例)
解析条件
本解析の最終目標を、参考文献の実験結果を再現することとして、光源のパワーを0.1Watts、解析光線数1.0E+5本で実行します。最終的に得る結果は、PPGセンサーが「受光した光線数」と「受光したパワー」です。心拍数モニターにおける時間変化を検証するため、複数回の光線追跡を実施します。まず、参考文献に基づき、心臓が収縮期に血液を送り出す際には、皮膚層内の血液量が拡張期と比べて2倍になるものと仮定します。
本解析では、血液量の相対値が「1 → 2 → 1」と変化する過程を1周期と定義し、この周期を5回繰り返すことで測定を行います。さらに、1周期を10ステップに分割し、各ステップにおいて光線追跡を実行します。つまり、合計で50回の光線追跡、すなわち50回分の脈拍測定を行うことになります。
図3は、本解析における血液量の相対値の時間変化をプロットしたものです。なお、本解析では計算負荷とのバランスを考慮して上記の設定を採用していますが、解析条件を調整することで、より細かな時間分解能や、より長い周期にわたる結果を得ることも可能です。
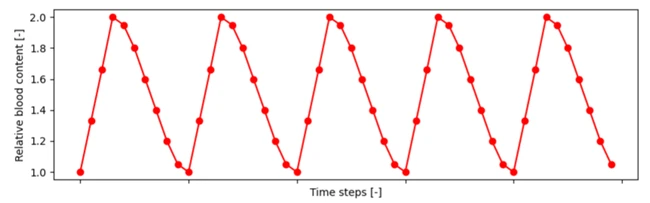
図3 : 血液量の時間変化
本解析では、各時刻の血液量に応じて各皮膚層の屈折率を再定義しながら光線追跡を実施します。各皮膚層の皮膚そのものの屈折率は一般に血液より高いため、血液量が増加すると、その層全体としての屈折率はわずかに低下します。
モデル化にあたっては、各皮膚層を「血液」と「皮膚組織」の二成分からなる均質な混合媒体とみなし、血液の体積比で屈折率や散乱のパラメータを線形補間して定義します(有効媒質の一次近似)。屈折率の場合、具体的には血液の体積比をfとすると、有効屈折率n_eff は
n_eff = f · n_blood + (1 − f) · n_tissue
と表します。
例えば網状層において、組織の屈折率が1.40、血液の屈折率が1.35、基準状態での血液含有割合が 5%(f = 0.05)であり、収縮期に相対量が2倍になると仮定します。このときの血液体積比は f = 0.05 × 2 = 0.10 となり、有効屈折率は
n_eff = 1.35 × 0.10 + 1.40 × (1 − 0.10) = 1.395
となります。このようなパラメータの再定義を、各ステップの光線追跡ごとに全ての皮膚層へ適用します。
解析結果
実際のモデル
図4は実際のモデルと光線の様子です。散乱の度に光線の色が変わるように描画しています。スマートウォッチのPPGから出射される光は、腕の皮膚の中でこのようにさまざまな方向へ伝搬していくことがわかります。
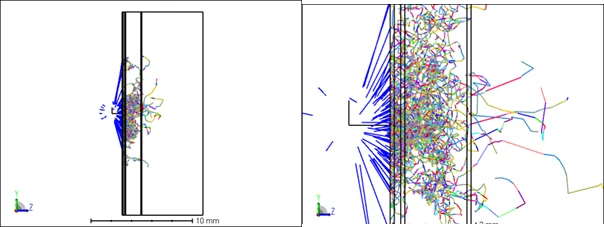
図4 : 皮膚の中を光線が伝搬する様子 (右図は拡大版)
図5は、光線が皮膚の中を伝搬したのちに、PPGセンサーへ入射した様子です。オレンジ色にハイライトされている小さい四角形がPPGセンサーです。今回の解析ではこのような光線を受信して脈拍測定を行っているわけです。
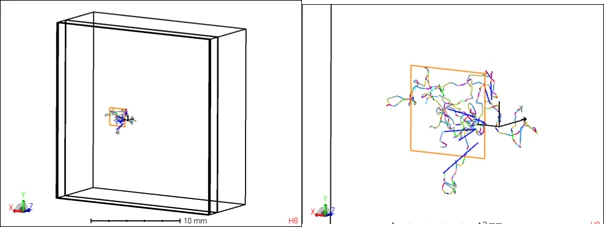
図5 : PPGセンサーで受光される光線
結果の評価
本解析では、1心拍を10ステップで表現し、それを5周期繰り返すことで、合計50回の光線追跡を実施しました。各ステップでPPGセンサーが受光した「光線数」と「受光パワー」を取得しています。これらの繰り返し処理と結果の集計は、PythonとOpticStudioのAPI連携により実行しました。その結果を図6に示します。
表2のとおり、血液は他の皮膚組織と比べて吸収係数が大きく、また異方性パラメータgは0.98 と前方散乱が卓越しています。したがって血液量が増えると、光は組織内でより強く吸収され、かつ前方へ散乱しやすくなるため、多重散乱の過程でPPGセンサーへ戻ってくる光が相対的に減少します。血液量が少ない場合はその逆で、検出器に到達する光線数と受光パワーはいずれも増加します。
図6の挙動はこの傾向をよく示しており、血液量が少ないときには受光光線数が多く受光パワーも大きく、血液量が多いときには受光光線数と受光パワーはどちらも小さくなります。今回の解析では、受光パワーから評価した信号変化量は、脈拍(血液量)の変化に対して概ね10~15%程度であることが分かりました。脈拍測定では、この信号の時間変動から実際の心拍数を算出します。
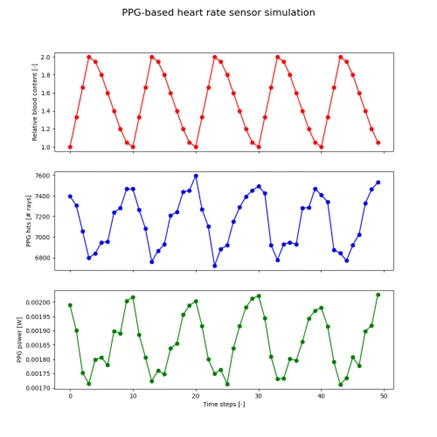
図6 : 脈拍測定の各種時間変化の様子
上(赤プロット) : 相対的な血液量(1.0~2.0)
中(青プロット) : PPGセンサーで受光した光線本数
下(緑プロット) : PPGセンサーで受光したパワー
まとめ
本事例では、既報の実験・数値研究を参考に、Ansys Zemax OpticStudioのノンシーケンシャルモードを用いて人間の皮膚を多層構造としてモデル化し、スマートウォッチ等に搭載されている反射型PPG(光電式容積脈波)による脈拍計測原理を再現しました。
皮膚各層における血液量の時間的変化に応じて、屈折率および散乱・吸収パラメータを更新しながら光線追跡を反復的に実行することで、検出器に到達する戻り光強度の周期的変動を取得し、脈拍信号の生成過程を数値的に再現しました。
本手法により、血液量変動と皮膚光学特性の関係を物理モデルとして明示的に扱うことが可能となり、PPGセンサーの信号生成メカニズムを定性的かつ定量的に理解するための基盤を示しました。今後は、波長依存性や個人差を考慮したパラメータ拡張を行うことで、実デバイス設計や信号最適化への応用が期待されます。
関連記事と参考文献
[発行日] 2026 年 2月
[発行元] サイバネットシステム株式会社 技術開発本部 デジタルエンジニアリング第1統括部