マルチスケールCAE ～数値材料試験のススメ～

東北大学大学院工学研究科 土木工学専攻
寺田 賢二郎

1．はじめに

すべての材料は微視的に見れば異種材料が組み合わさってできた複合材料です。“微視的”の程度にも依りますが、合成ゴムや樹脂、金属はμm以下のオーダーで非均質性が卓越しています。
また、多孔質セラミックスは数μmからmmオーダーの孔を有する非均質材料、コンクリート材料もmmからcmオーダーで骨材とモルタルからなる2相複合材料とみなすことができます。

しかし従来のCAEでは、このような微視的に観察される非均質な内部構造の存在は認めながらも、その影響はすべて材料試験で得られる計測データに反映されるであろうと期待しながら（あるいは気にとめることなく）解析が進められます。

本稿では、この材料内部の（ミクロスケールの）構造に着目した“CAEのあるものづくり”を紹介します。具体的には、ミクロ構造を解析対象とすることで、(a)等価な（マクロスケールの）力学特性値の算出と、(b)これを用いた全体構造物（マクロ構造物）の解析結果を反映させたミクロ構造物の応答評価を可能にする、「マルチスケールCAE」について述べます。

2．シングルスケールCAEのための材料試験

一般的な材料試験を思い出してみましょう。材料種別に応じた材料特性を計測するために、できる限り境界や治具の影響が出ないように、またできる限り理想的な載荷条件となるように供試体形状を決め、実験条件を整えます。換言すれば、材料の非均質性を特徴づける"微視的な構造特性"のみが見かけの応答に反映され、供試体形状や支持・載荷状態の影響は小さいものと期待して"巨視的な材料特性"を計測します。

例として図1(a)に示すように軟らかい材料と剛な材料が交互に繰り返されてできた1次元構造物を考えましょう。この繰り返し構造の最小単位をユニットセルといいますが、材料の微視的な内部構造（すなわち微視構造あるいはミクロ構造）であって、構造全体からすれば非常に小さいものと仮定できます。また、この2つの異なる材料の構成則とその材料パラメータ（ここでは線形弾性体の構成則でパラメータはYoung率）は既知と仮定します。

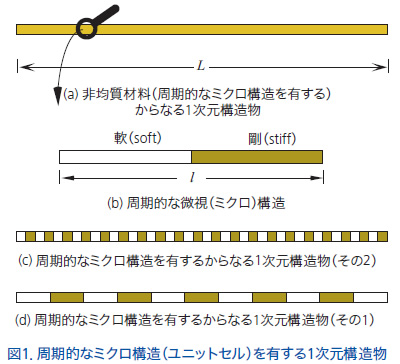
まず、図1(a)の構造体の軸方向の弾性率を知りたければ、これを供試体と 考えて素直に荷重を加えてみることでしょう。供試体の端面で測られる荷 重（あるいはロードセルで測った応力値）と変位（あるいは変形後の長さ をとしたときのひずみの関係，すなわち次式から容易 に見かけの剛性（ここでは平均的なYoung率）を計測できます。

さてでは、全体構造中のミクロ構造の個数が異なる図1(c)や(d)の構造物に対して、同じ理想的な条件で載荷すればどうでしょう？ここでは厳密な議論は避けますが、得られる荷重・変位関係は図1(a)の場合と同じになります。
このことは、供試体とみたてた図1(a)の構造物について“理想的な”条件下で計測される材料特性は、繰り返しの数に関係なく、ユニットセル単体（図1(b)）に対して行った供試体試験の結果と同じであることを意味します。
つまり、この軟・剛な材料が繰り返された複合材料の巨視的材料特性はユニットセルを供試体として"理想的な"載荷条件の下で材料試験を行えばよいのです（このようなミクロ構造を代表体積要素（RVE）と呼んでいます）。
しかし実際は、(1)ユニットセルは非常に小さいので供試体を生成するのは一般に困難ですし、(2)治具や計測器、そしてユニットセルの幾何形状（つまり境界条件）の影響を排除した理想的な実験は残念ながら不可能です。
そこで、以下では理想化された条件の下での構造物の応答解析を得意とするCAEの適用を考えましょう。つまり、ユニットセル（ミクロ構造）の数値モデルを生成してこれを供試体とみたてた数値実験を行い、得られる解析結果を材料試験の結果とみなしてデータ整理することで、その"微視的な構造特性"を反映した構造物全体の（シングルスケールの）CAEを実現するための"巨視的な材料特性"を評価するのです。

3．ミクロ構造に対する数値材料試験

図1(b)のユニットセル（座標系を導入した物理領域は領域 ）を“数値供試体”モデルとしてCAEソフトにより実験を模擬した構造解析を行うことを考えます。均質化法の理論によれば、この数値実験に対応する支配方程式は次のように与えられます（ただし、断面積は1）1）。

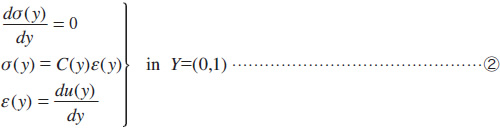
ここで、はデータとして“数値供試体”の端面（境界）に与えるマクロひずみです。また、これをCAEソフトで解析するという観点では、ミクロ構造の数値モデル（例えば，FEMメッシュ）と、2つの異なる材料のYoung率が用意されていなければなりません。未知変数は、ミクロスケールの変位、ひずみ、および各相のYoung率とミクロひずみから算出されるミクロ応力の3つです。

さて、このユニットセルという供試体に対する数値実験の第１の目的は、マクロな応力とひずみの関係式（つまりマクロ構成則） における係数（均質化Young率 ）を求めることです。ただしここで、このマクロ応力とひずみは、それぞれミクロ応力とひずみのユニットセルでの平均値であることが理論的に証明されています1）。つまり、および （ただし、）なのですが、このユニットセルに対してデータを与えた構造解析から得られるミクロ応力 に対するポスト処理の一環としてその平均値 を算出して、これをロードセルによる“数値供試体”の端面の応力の計測値とみなせば、結果として均質化Young率はのように求められます。実験を数値的に模擬しているので形式的には式①と同じ式が得られ、目的が達成されることになります。このような考え方は、実は多次元問題においても成り立ちます。すなわち、非均質（複合）材料を特徴づけるミクロ構造（＝ユニットセル＝RVE）の数値モデルを生成して適切な境界条件を与えて解析を実行し、ポストプロセスにおいて応力値のユニットセル領域内平均を計算すれば、平均的な材料特性が求められることになります。例えば、図2(a)に示すような2種類の線形弾性体からなるミクロ構造（の有限要素モデル）を有する複合材料を対象として、均質化（マクロ）構成則 における均質化弾性 係数行列 を算出することを考えます。ここで、はマクロひずみ、はマクロ応力です。このモデルに対して、平面ひずみの仮定で

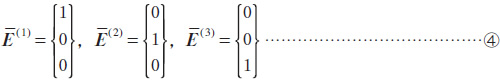
の3種類のマクロひずみをデータとして与える数値実験を行い、解析結果と して得られる図2(b)、(c)、(d)のミクロ応力のユニットセルでの体積平均を取れば、

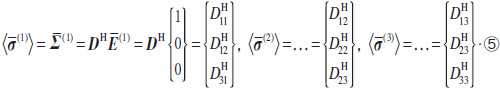
となるので、マクロスケールで異方的な弾性特性を表す均質化弾性係数行列 が算出できます。そして次に、得られた を用いてマクロモデルの構造解析（図2(e)、(f)）を従来のCAEの枠組みで実施することになります。
さらに、ミクロ構造の数値モデルに対する解析は（上記の単位マクロひずみだけではなく）任意のマクロ変形（ひずみ）をデータとして用いても実施できるので、必要に応じてマクロ解析結果として得られる各マクロ物質点のひずみを用いたミクロ解析を行えば、この点のマクロな材料挙動を特徴づけているミクロ構造の実際の応答を評価できます。たとえば、図2(g)はマクロ解析結果として得られた、あるマクロ物質点でのひずみをデータとしてミクロ解析を行った際のミクロ応力分布です。
以上、紙面の関係で線形弾性体の静的な力学挙動を題材にして数値材料試験について説明しましたが、その道具立てとしての均質化法に基づくマルチスケール解析法は、様々な物理現象や非線形問題に適用できる汎用的なものです。

※画像をクリックすると拡大表示します。

4．CAEの新しいカタチ ～マルチスケールCAE～

コンピュータハードウェア・ソフトウェアの高性能・高機能化、そして理論面の整備を背景として、FRPなどに代表される複合材料を中心とした「材料を設計変数にとる“CAEによるものづくり”」2）が可能となりつつあります。その場合、自ずと工業製品に利用される材料の性能に対する要求は高まり、利用目的に応じた所望の物理特性や機能を生み出すための材料設計が一般的になると考えられます。

材料設計には材料組成や製造プロセスを変化させる材料科学的なアプローチもあれば、個々の構成材料の形態や分布性状を決定する材料力学的なアプローチもあります。これらの新しい材料設計案は比較的容易に作成できますが、その一方で、実際の材料データ取得のための材料試作や材料実験等に掛かる労力やコストは膨大なものになります。
このため、材料実験をベースにしたミクロ構造の設計作業をCAEで代替するという考え方が生まれるのはごく自然な流れです。先に例示したミクロ構造に対する数値実験はその一環ですが、ちょうどマクロ工業製品に対するCAEの発展と経緯と同じなのです。また、このCAEによる数値材料試験では、先に触れたようにある理想化された条件下で材料挙動を特徴づけることができますので、結果は材料設計だけでなく製造・加工時における参照値（または目標値）として利用可能なのです。
このことは、材料試作や材料実験等に内在する誤差を排除し、開発者・設計者が材料の真の特性を導出することができ、適切な材料選択や設計した材料の適切な使用方法を示すことにつながります。さらに、このミクロ構造の数値解析は、先の2次元の数値例で示したようにユニットセルの構造体として力学挙動を特徴づけることに他ならないので、実際の実験のように見かけの（つまり巨視的）計測データを収集するだけでなく、そのマクロ特性が発現するミクロなメカニズムを調べたり、マクロ構造の解析結果を反映してユニットセルがどのように振る舞うかを予測できたりできるのです。マクロ構造とともにミクロ構造も同時に"ものづくり"の対象として捉えた新しいCAEのカタチと言えるのではないでしょうか。

5．おわりに

従来のマクロスケールのCAEにおいて、使用する材料のタイプ（材料カード）とその材料定数（パラメータ）は最も重要な入力データの一つです。まずは材料モデル（すなわち材料構成則）を選定して材料カードを決め、規格化された工業材料であればハンドブック値を、また特殊な材料であればその材料メーカーが提供する規格値を用いることになるでしょう。

しかし一方、材料メーカーや材料とともにこれを用いた構造物を製造するメーカーにとっては、その材料パラメータを得る必要があるので、材料実験はマクロCAEに先だって行わねばならないプロセスになります。本稿では、ミクロ構造の解析にCAEを適用す ることで、この材料実験を数値材料実験に置き換えることをおススメしました。