関連情報
Ansysを利用したマルチスケールCAE ~ Ansysを利用した数値材料試験 ~
日東紡績株式会社 グラスファイバー開発研究所
平山 紀夫
1.はじめに
著者がAnsysに代表されるCAEツールを使い始めてから、すでに15年以上
が経ちます。この間のCAEツールの進歩は目覚しく、今では、ほとんどの製造
業で商品開発・設計プロセスに不可欠のものになっています。特にこの数年
で、CAEツールによる数値解析技術が線形問題から非線形性の強い複雑な
物理現象を対象とするようになりました。なかでも構造解析の分野では、幾
何学的非線形はもとより、材料の非線形性、境界条件、荷重条件の非線形
をも考慮した解析が日常的に行われています。このことは、最近の企業の商
品設計や解析事例を見ても明らかで、今後もより複雑な非線形現象への解
析に積極的な挑戦が行われていくと思います。
しかしながら、著者の専門である材料技術の立場から見ると、製造業の開発現
場ではこのような非線形解析業務にかける労力と比較して、非線形材料特性の
算出や評価・把握が充分に行われているようには思えません。実際に、大学等の
公的な一部の研究機関を除けば、膨大な数値解析事例のなかで、材料の非線形
特性を積極的に解析に取り込んでいる事例は極めて少ないと思います。
「なぜだろうか?」と自問自答し、次の3つの理由にいきつきました。
- そもそも、異方性材料の非線形特性を正確に予測する解析的手段がなく、実験的にも算出が困難であるから
- 次に、何とかして実験的に異方性材料の非線形特性を計測できても、汎用のFEMプログラムに適切な異方性材料の構成式が具備されていないため解析ができないから
- そして、より本質的な問題として、多くの製造業の技術者達は商品開発の段階で用いる解析技術に、異方性材料の非線形特性までを考慮する必要はないと考えているから
これらのことは、多くの技術者が多かれ少なかれ感じていることではないかと思います。そして、1.と2.に関してはAnsysのようなCAEツールで解決したいと思われている技術者も多いのではないかと思います。
実は、著者もそのように強く考えている一人です。様々な異方性材料の時間や温度に依存した非線形性を計測できる試験システムが存在するのであれば、測定してみたい材料がたくさんあります。材料のクリープ特性や粘弾性も、計測する方向が異なれば全く異なる挙動を示すものがたくさんあります。まだ、我々が解析の対象として十分に取り扱えていないだけです。
このような異方性の非線形特性の計測には、東北大学・寺田助教授が提案されているようなマルチスケール解析技術を応用した数値材料試験が有用です(*1)、(*2)。
本解説では、東北大学・寺田助教授、(株)くいんと、サイバネットシステム(株)、と著者らで開発したAnsysを利用したマルチスケール解析システムと数値材料試験による材料物性の計測について解説します。そして、今年初夏にサイバネットシステム(株)から販売が予定されている、Ansysを利用したマルチスケール解析システムの線形バージョンについても紹介します。
2.Ansysを利用したマルチスケール解析システム(線形バージョン)
2.1. 数値材料試験としての均質化解析
均質化法を使用したマルチスケール解析技術では、その解析の一部で均質化と呼ばれる解析過程があります。実は、この均質化と呼ばれている解析が、複雑な構成をしている材料の等価な材料物性値を算出する数値材料試験に相当します。
詳しくは、文献(1)をご一読されたいと思いますが、ここでは簡単な構造問題を例にしてAnsysで解析を行う場合の考え方の一例を示します。
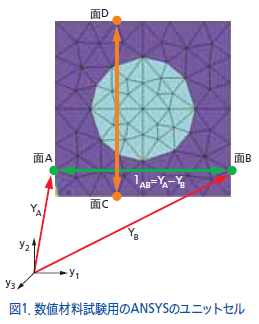
図1に示すようなユニットセルのFEMモデルを考えます。このユニットセルが材料のミクロな構造だと仮定しましょう。
この図のようにミクロ構造は“非均質性”をもっていますので、マクロ構造が荷重を受けて変形した時に、ミクロ構造の変形は非常に複雑な変
形をすることになります。
ところが、均質化法の理論によれば、その複雑なミクロ構造の変形も"平均的"に見ることでマクロ構造のある一点での変形と対応づけ
ることができます。
具体的には、ミクロ構造の複雑な変形は、ミクロ構造に一様に作用する平均的な変形成分(マクロ変形と一致する変形成分)と、平均すると消えてゼロになる変形成分(これが非均質性に起因して発生する変形成分)に分解して考えることができるのです。
したがって、テンソル表示でミクロの変位関数は一様変形と非均質性に起因して生ずる周期的な擾乱変位の和として次式で与えられると仮定できます。
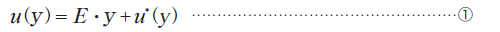
図1に示すユニットセルの境界での周期性を有するy1方向の相対する面をA面とB面とすると、これらA面、B面上での変位は、それぞれ、
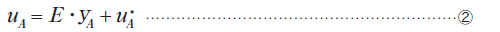
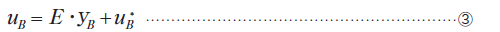
となります。ここで、ミクロ変位の周期性より、
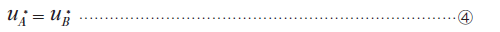
なので、
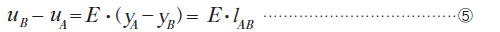
となります。
わかりやすく表現するため、⑤式をミクロ座標系における成分表示にすると
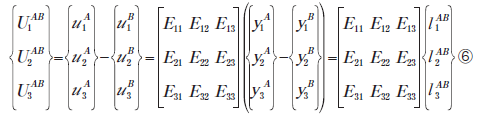
となります。別の面C、面D上の点でも、面E、面F上の点でも、同様な考え方でまとめられます。
実際のAnsysでの解析では、この(6)式において、ユニットセルの境界での周期性を有するy1方向の相対する面(A-B面)の変位関係![]() 等を拘束方程式で与えることになります。そして、例えばユニットセルにy1方向の単位ひずみ
等を拘束方程式で与えることになります。そして、例えばユニットセルにy1方向の単位ひずみ![]() だけを与えたい場合には、(6)式に
だけを与えたい場合には、(6)式に![]() 、その他は
、その他は![]() を代入し、対応する拘束方程式を算出します。
を代入し、対応する拘束方程式を算出します。
この変位拘束関係をAnsysに与えて、6方向のユニットセルのFEMモデルの解析を行います。求まったミクロ構造の変位は、結果的に一様変位と非均質性による周期的な擾乱変位の和になります。そして、線形問題では、この解析結果からユニットセルの応力を積分してユニットセルの体積平均を取ると均質化されたユニットセルの弾性定数を求めることができます。
2.2. マルチスケール解析としての局所化解析
マルチスケール解析技術では、前章の数値材料試験に相当する均質化解析の過程とその後段の解析プロセスとして局所化解析があります。すなわち、局所化解析には数値材料試験を行い算出した均質化物性値でマクロ解析の対象となる製品の解析を行った後に、その製品に発生しているマクロなひずみレベルから材料内部のミクロな応力状態を観察したいという気持ちがこめられています。
このような解析機能への要求は、製品の設計者というよりは材料開発者や研究者に多く存在するかもしれません。
Ansysによる局所化解析では、マクロ解析をした製品の解析結果から、ミクロ構造内部の応力状態を観察したい任意の場所の歪Eをとりだします。そして、式(6)により再度、変位拘束関係をAnsysに与えてユニットセルのFEM解析を行うことになります。このようにして解析したユニットセルの応力は、マクロ的なひずみと周期的なミクロ擾乱ひずみの両方に起因して材料内部に発生する実際の応力に
なります。
以上簡単ですが、数値材料試験に相当する均質化解析と局所化解析についてAnsysを使用して解析する概略の方法を説明しました。
次節では、実際に開発したAnsysを利用したマルチスケール解析システムについて説明をします。
2.3. Ansysマルチスケール解析システム(線形バージョン)
(1)GUIとミクロモデルの作成機能
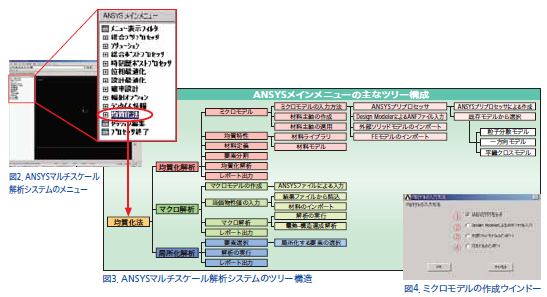
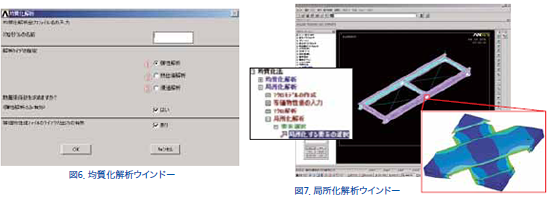
Ansysには、Ansysのメインメニューをユーザーが自在に操作できるように、プログラミング言語が用意されています。今回の開発ではこのプログラミング言語を使用して、Ansysのメインメニューに均質化解析と局所化解析のメニューの組み込みを行ないました。こうすることで、マルチスケール解析システムのすべての機能をAnsysの既存の操作方法で利用できます。実際に組み込んだマルチスケール解析システムのメニューを図2に示します。また、解析システムのメニューのツリー構造を図3に示します。
この開発する解析システムでは、システムを利用するユーザーが、その都度ミクロモデルの作成や要素分割を行う手間を省き、短時間で材料の等価物性値が算出できるように、ミクロモデルの自動作成機能と材料データベースを付加しています。また、任意のCADでミクロモデルの要素分割を行なったモデルでもこの解析システムで対応ができるように、非周期対称メッシュモデルへの周期対称条件の自動生成機能も持っています。図4にミクロモデルの作成ウィンドウを示し、図5には外部モデルデータにより入力できる材料データの一例を示します。これらの機能は、ミクロ構造のFEMモデルの作成が、マルチスケール解析全体の負荷を増大させることのないように配慮したものです。今後は、このようなミクロ構造の簡易モデリング機能の開発を進め、画像によるミクロモデルの生成ツールも提供したいと考えています。

(2)均質化機能
Ansysでミクロ構造を定義した後に、ミクロ構造を構成している個々の材料の物性値を入力し、その後、ミクロ構造の要素分割を行なえば数値材料試験、すなわち均質化解析を行う準備ができたことになります。Ansysの均質化解析メニューのなかから、均質化解析の実行を選ぶと、図6に示す均質化解析のメニューが現れます。現在のバージョンでは解析タイプを指定することで、次の3種類の均質化解析が実行でき、異方性のマクロ等価物性値が計算できます。
- 弾性解析 → 9つのマクロ弾性係数、ポアソン比と3方向のマクロ線膨張係数
- 熱伝導解析 → 3方向のマクロ熱伝導率
- 浸透解析 → 3方向のマクロ浸透係数
(3)局所化機能
均質化解析で算出したマクロ等価材料物性値を使用してマクロ構造の解析を行った後、マクロ応力の高いところでミクロ材料の内部にどの程度の応力やひずみが発生しているかを知りたいことがあると思います。たとえば、繊維で強化した高分子系の複合材料では、マクロ的な応力レベルはそれほど高くなくても、ミクロ構造内部ではマトリックスである高分子材料が塑性域に達するような高い応力やひずみが発生していることがあります。このようなケースでは局所化解析が有用な機能であり、従来では安全率など不明瞭な係数で回避していた設計に対して、新しい安全性評価のためのヒントを与えてくれると期待しています。
Ansysのマルチスケールシステムの局所化解析機能では、局所化したい任意の要素を選択した後、積層要素であればレイヤー番号とレイヤー位置を指定することで、簡単に局所化解析が実行できるようになっています。図7には、Ansysのマルチスケールシステムの局所化解析機能で、マクロ構造のひずみデータからミクロ材料の内部に発生している応力レベルを計算した例を示します。この図に示すように、構造解析であればその位置における各軸方向のひずみより、局所化解析が実行され、その結果はAnsysのポストプロセッサ機能を用いて可視化可能になっています。
3.Ansysマルチスケール解析の事例
3.1. 線形解析の事例
開発したAnsysマルチスケール解析システムの解析事例をいくつかご紹介します。
(1)構造解析
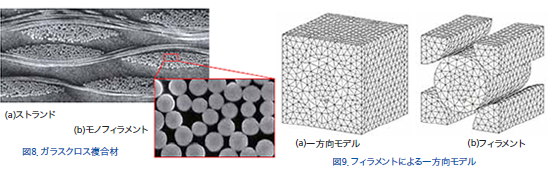
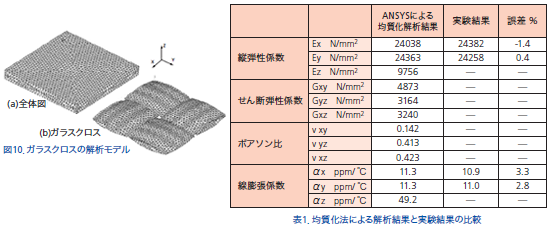
構造解析の事例としては、GFRP(ガラス繊維強化プラスチック)のマクロ弾性係数とマクロ線膨張係数の算出例を紹介します。この材料は、エポキシ樹脂をガラス繊維束で織ったクロス材で強化したもので、高分子系複合材料の代表的なものです。このガラスクロス複合材は、図8に示すように、直径10μのガラス繊維が数百本収束したストランドという単位で織り構造が形成されています。そのため、単純に2本の縦糸と横糸のガラス繊維が織られているようなモデル化はできません。このようなケースの解析モデルでは、ストランドは図9に示すフィラメントによる一方向材が周期的に配置されていると仮定し、一度均質化解析を行いストランドの異方性のマクロ等価材料物性値を算出しなくてはなりません。そして、算出したストランドの異方性のマクロ等価材料物性値を図10に示す織り構造の縦糸、横糸のストランドに適用して再度均質化解析を行います。このように2回の均質化解析を行うことで、ガラスクロス複合材の異方性のマクロ等価材料物性値を算出することができます。
表1にAnsysによる均質化解析結果と実験結果を比較して示します。表1より、解析結果は弾性係数及び線膨張係数ともに実験結果とよく一致し、開発した均質化解析機能の妥当性が確認できます。なお、局所化解析に関しては、均質化解析と同じ解析ルーティンを使用していることや実験による検証が難しいことから実験値との比較検証は行っていません。
(2)浸透解析
浸透流の解析の事例として、一方向に繊維が並んだ間を樹脂が浸透していく解析を行い、均質化解析の妥当性を検証してみました。この一方向に繊維が並んだ間を樹脂が浸透していく問題には、理論的な解析解が示されているからです。
円形断面の一方向繊維材料の横方向の浸透係数に関しては、Gebartが次 式に示すように理論的な算出式を導いています(3)。
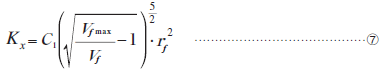
ここで、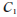 は次式で計算でき、
は次式で計算でき、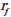 は繊維半径、
は繊維半径、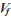 は繊維体積含有率、
は繊維体積含有率、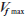 は最密繊維体積含有率です。
は最密繊維体積含有率です。
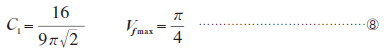
⑦式で示した理論解とAnsysによる均質化解析結果とを比較して図11に示します。解析結果は幅広い繊維の含有率で理論解とよく一致し、浸透係数に関しても開発した均質化解析機能の妥当性が確認できました。このような多孔質媒体中の浸透流の解析は、極めて応用範囲が広いと考えています。Ansysのプロダクトファミリーの流体解析ソフトである、FLOTRANやCFX-5では、この均質化解析結果のマクロ浸透係数をそのまま分布流体抵抗値として入力して解析を行うことができます。
3.2. 非線形解析への拡張
最後に、非線形解析への拡張についてふれたいと思います。今回開発しているAnsysマルチスケール解析システムは、非線形問題への拡張を前提としています。現在、開発を予定しているものは、次の3つのタイプの材料非線形解析機能です。
- 塑性
- 粘弾性およびクリープ
- 超弾性
どの機能も数値解析的にはとても難易度の高い高度なものです。本解説では、粘弾性特性を同定した数値材料試験の解析事例を紹介し、均質化法を材料非線形問題に応用する“ねらい”と“課題”について述べたいと思います。
(1)粘弾性解析のねらい
一般的な高分子系の複合材料や繊維で強化したゴム材料の応力緩和現象やクリープ現象は、その複合材料を構成しているマトリックス成分の粘弾性挙動に支配されます。一般的には繊維のような強化材料は、無機系の材料が多く粘性項は無視できることが多いからです。このような複合材料の粘弾性特性が、マトリックス成分の粘弾性挙動から予測できると非常に有意義です。なぜなら、一度、マトリックス成分の粘弾性挙動を測定し材料定数を算出しておけば、そのマトリックス成分と様々な比率や形態で強化材料を複合化した材料の時間や温度に依存した特性が、試験をしなくても予測できるようになるからです。また、様々な粘弾性挙動を有するポリマー成分を ブレンドするようなケースでも、複合された材料の粘弾性挙動を試作前に予測し、製品の減衰特性等の設計に積極的に利用するといったことも可能になるかも知れません。
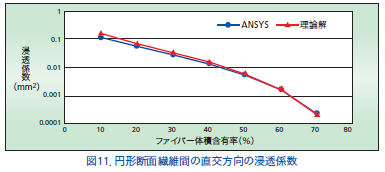
特に、異方性を有する粘弾性材料の時間や温度に依存した特性を測定するには、試験片作成にもそれなりの労力を覚悟しなくてはなりませんし、測定精度や測定時間も単一材料と同じでは済みません。今回は、このように、異方性を有する粘弾性材料の時間や温度に依存した特性をマトリックス成分の粘弾性挙動から予測することを目的に、均質化法を粘弾性解析に適用した事例を示します。図12に解析に用いたマトリックス樹脂の動的粘弾性試験から求めた緩和弾性率のマスターカーブを示します。この樹脂は特殊な熱可塑性のエポキシ樹脂で、この樹脂をマトリックスとして、強化繊維には一方向に引き揃えられた炭素繊維を使用して、一方向強化のCFRP(炭素 繊維強化プラスチック)を試作しました。図13にCFRP断面の走査型電子顕微鏡(SEM)写真を示します。この写真は、CFRPの繊維軸方向と直角の方向に切断した断面写真です。このCFRPの垂直方向の粘弾性挙動を均質化法による数値的な粘弾性試験で予測しました。
(2)粘弾性解析の結果と課題
解析の方法としては、一方向強化CFRP材のユニットセルを作成し、繊維直角方向に一定荷重を作用させる応力緩和現象と、動的に正弦波入力を与える動的粘弾性試験の2つの方法で行なっています。
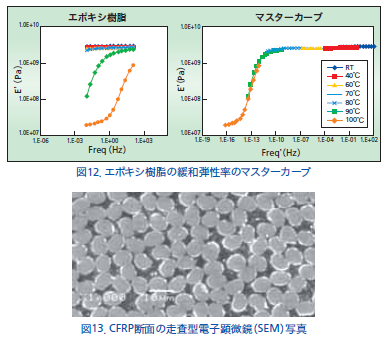
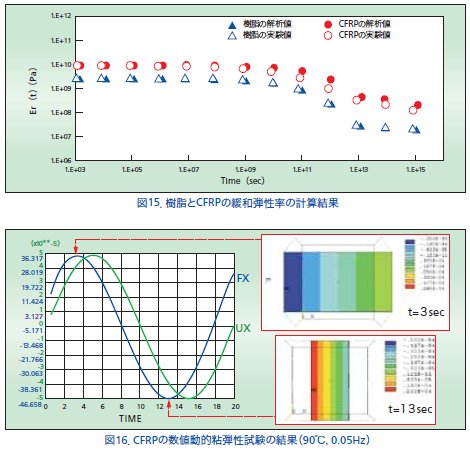
図14に、一方向強化CFRP材のユニットセルに繊維直角方向に一定荷重を作用させた時の応力緩和の様子を示します。そして、図15には実際に樹脂とCFRPの両方で行なった実験結果とAnsysによる数値材料試験を比較して示します。CFRP材のユニットセルを用いて数値材料試験から算出した緩和弾性率は、若干の誤差はありますが実験から求めたCFRPの緩和弾性率と幅広い時間域でよく一致しています。また、図16には動的粘弾性試験の解析例として、雰囲気温度が90℃で繊維直角方向に0.05Hzの正弦波入力を与えた時のCFRPの荷重と変位の位相差を示します。この位相差の情報は材料が持つ減衰特性の予測を行う際には重要なファクターとなります。この位相差は動的粘弾性試験では![]() (貯蔵弾性率と損失弾性率との比)として計測されますが、今回の解析結果は実験結果とよく一致していました。
このように、均質化法を非線形解析の領域まで応用すると、従来では計測が困難であった材料の特性予測が可能となってきます。ただし、今回のように異方性を有する粘弾性材料の特性が算出できるようになっても、現状のAnsysでは異方性の粘弾性挙動の解析を行なうことができません。他のソルバーでも異方性主軸の各軸方向における粘弾性挙動を単に係数比で入力するだけの機能しか備わっていないことがほとんどです。このような場合にはユーザーサブルーティンで機能を拡張することになりますが、適切な構成則を決定し入力できるかが今後の大きな課題です。
(貯蔵弾性率と損失弾性率との比)として計測されますが、今回の解析結果は実験結果とよく一致していました。
このように、均質化法を非線形解析の領域まで応用すると、従来では計測が困難であった材料の特性予測が可能となってきます。ただし、今回のように異方性を有する粘弾性材料の特性が算出できるようになっても、現状のAnsysでは異方性の粘弾性挙動の解析を行なうことができません。他のソルバーでも異方性主軸の各軸方向における粘弾性挙動を単に係数比で入力するだけの機能しか備わっていないことがほとんどです。このような場合にはユーザーサブルーティンで機能を拡張することになりますが、適切な構成則を決定し入力できるかが今後の大きな課題です。

4.おわりに
最初に述べましたように、今回のAnsysマルチスケール解析システムは材料非線形現象をより深く理解し、その知見をマクロな数値解析や製品設計に反映させたいという願いをこめて開発しています。したがいまして、Ansysマルチスケール解析システムの均質化解析機能も材料の異方性の非線形特性の計測を行えることを強く志向しています。なぜなら、材料の異方性の非線形特性の計測をする場合、現状の実験を主体とした方法には以下のような課題があるからです。
- 任意の材料をブレンドする複合材料では、材料実験のための試料作成自体が困難な場合が多く材料試験自体ができないことがある。
- 材料試験片が加工できても、試験片の厚み方向の特性や面外のせん断特性等の非線形挙動は実験では計測が難しい。
- そして、実験で計測できる方向に限って測定しても、試料作成時のバラツキや試験の精度の問題で、真の非線形材料特性の取得が困難であるケースがある。
- さらに、異方性を示す材料の非線形領域のデータ収集には、膨大なコストと労力がかかる。
「材料の異方性の非線形特性の計測が数値解析で行える」ということは、多くの技術者の知的好奇心を満たすだけではなく、これらの4つの課題に対して現実的な回答を与えることのできる数少ないアプローチであると思います。この現在開発中のAnsysを使用したマルチスケール非線形解析のシステムは、著者が検証した事例において数値材料試験としては実用的なレベルであると思います。ただし、実用化に向けては次のような大きな課題を残しています。
- 超弾性材料等における解析の収束性
- 同定された異方性材料特性の構成則の決定とその入力手段
特に、構成則の決定に関しては、重大な課題です。なぜなら、異方性の非線形材料特性が数値材料試験によって同定されても、その材料特性を使用してマクロ解析を行う場合には、対応する適切な構成式が用意されていなくてはならないからです。しかしながら、現状の汎用FEMソフトに具備されている構成式はごく少数で、同定された異方性の材料特性が表現できない可能性があります。今後は、この課題について検討を進め、適切な時期に研究の成果を公開したいと考えています。
参考文献
*2:寺田賢二郎:マルチスケールCAE~数値材料試験のススメ~,CAEのあるものづくり,サイバネットシステム,Vol.5,p.9-10,2006
*3:B.R.Gebart, Journal of Composite Materials, Vol.26,No.8(1992), PP.1100-1133.



