資料ダウンロード
数値材料試験による異方性非線形材料特性の算出（2）
繊維強化プラスチックのマルチスケール解析
CAEのあるものづくり Vol.11｜公開日：2009年9月
目次
はじめに
前稿 1） では、繊維強化プラスチック（以下、FRP）の微視的（ミクロ）構造と巨視的（マクロ）構造の力学的相互作用の評価を意図して、マクロ材料特性を把握するための「数値材料試験」、すなわちミクロ構造に対する“均質化解析”に用いるプラスチック（エポキシ樹脂）の材料試験データの計測手順と、データ処理・分析について説明しました。本稿では、このプラスチックを母材に用いたFRPのマクロ的な材料挙動を表現可能な異方性粘弾性構成則を提示し、その材料パラメーターを数値材料試験により同定する方法を解説します。また、そのFRPの供試体をマクロ構造物とするクリープ試験の“マクロ解析”を行い、実験結果と比較することで提示した構成則を検証するとともに、その変形履歴を反映したミクロ構造の応答を再現する“局所化解析”の一例を紹介します。
この均質化解析ーマクロ解析ー局所化解析という一連の解析を（均質化理論に基づく）「マルチスケール解析」と呼んでいますが、その理論の詳細については文献 2） 等を、数値材料試験の考え方や方法については文献 3）～ 5） 等を参照して下さい。
異方性粘弾性構成則
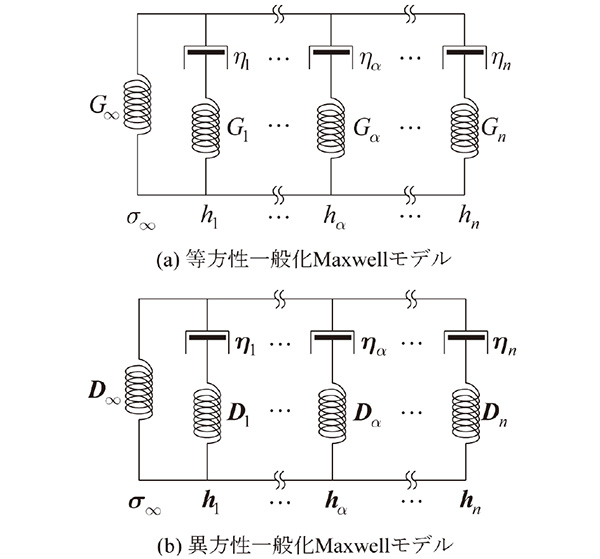
図1 一般化Maxwellモデル
前稿 1） では、一般に広く利用されている等方性一般化Maxwellモデルを、FRPミクロ構造内の母材（プラスチック）の粘弾性特性として用いて数値材料試験を行いました。その数値材料試験で得られたマクロ応力緩和応答が異方性を示したことをから、本稿では等方性一般化Maxwellモデルを異方性粘弾性体に拡張したモデル 6） を紹介し、マクロ構成則として採用することにします。
2.1 “等方性”一般化Maxwellモデル
Ansys等の汎用FEMコードでは一般に、一般化Maxwellモデルが等方的な粘弾性モデルとして用意されています。このモデルは図1（a）に示すような“ばねーダッシュポット”系を想定して、時間tに関する緩和（せん断）弾性率を
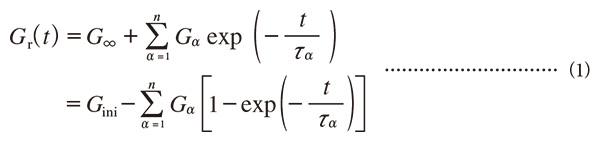
と与えます。ここで、G ∞ 平衡応力に関するせん断弾性係数、G ini = G ∞ ＋Σ α G α は初期せん断弾性率、G α とη α はそれぞれMaxwell要素αのせん断弾性係数と粘弾性係数です。また、緩和時間t α は次式で定義されています。
このモデルは、前稿 1） でプラスチックの材料モデルとして採用したものであり、同定された材料パラメーターは数値材料試験に際しての入力データとなります（文献 1） の図5を参照）。
通常は、応力の静水圧成分は粘弾性挙動を示さないと仮定するので、緩和試験を想定して一定ひずみ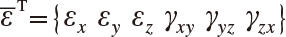 
を与えると、応力 
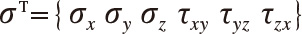は、
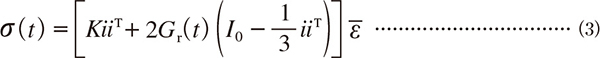
と計算されます。ここで、添え字“T”は行列・ベクトルの転置を表し、Kは（時間に依存しない）体積弾性係数です。また、iやI 0 は次式で定義されています。
この式（3）に緩和せん断弾性率（1）（第1式）を代入すると、次式のように応力の平衡部分σ ∞ と非平衡部分Σh α （時間とともに緩和する成分）に分解できます。
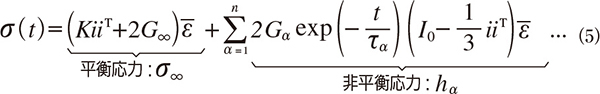
2.2 “異方性”一般化Maxwellモデルへの拡張
前稿 1） では、FRPの母材であるプラスチックには前節で示した等方性一般化Maxwellモデルを用いて、繊維は粘弾性挙動を示さない弾性体とみなしました。そして、そのFRPミクロ構造に対して数値材料試験を行うと、マクロ材料挙動としては異方的な粘弾性応答が得られることを、前稿（1）の図7で示しました（図2）。本節では、そのような異方性粘弾性挙動を表現できる構成則として、前節の一般化Maxwellモデルを拡張したモデルを紹介します…
