CAEを学ぶ
逆解析による実験と解析の合わせ込み
~4点曲げ試験による検証事例~
はじめに
この記事をお読みいただいている皆様の多くは、AnsysをはじめとするCAEツールを実際にご利用されている方だと思いますが、解析結果が実験と定量的または定性的に合わないという経験を何度もされているのではないでしょうか?
CAEツールは入力データと設定した理論に則って結果を出しているだけの電卓のようなものですから、ソフトの不具合や実験の失敗といった解析以外の原因を除くと、実験と合わない原因のほとんどは以下のいずれかによるものになります。
- 原因(1):単なる操作ミス
- 原因(2):設定した理論では現象が表現できない
- 原因(3):入力条件が現象を再現していない
解析専任者がよく使用するツールは物理現象の再現性を高めるために設定項目が多く、原因(1)の操作ミスが発生しやすくなりますが、これはそのツールを用いた解析経験や、入力後のチェックを慎重に行うことである程度防ぐことができます。
次に原因(2)は、例えば「大変形理論での計算が必要な問題に微小変形理論を用いている」「必要な精度が得られる要素分割を行っていない」といったことが挙げられますが、これも原因としては比較的特定しやすく、多くの場合修正も容易です。
最後に原因(3)ですが、これは(1)(2)がクリアされた状態でも発生するものであり、正しいと考えて入力した解析条件が実は現象を再現していないという状態を指します。
なぜこのような状態になるかというと、解析モデル作成者が意識せずに結果に影響を及ぼす要因をモデル化から省略してしまうことによるものが多いようです。
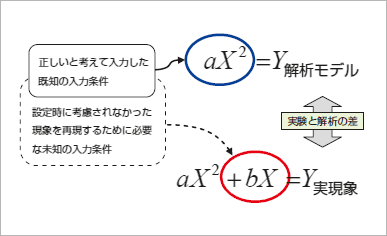 原因(3)を簡単な数式で表した概念図
原因(3)を簡単な数式で表した概念図 これは、例えば片持ち梁の曲げをモデル化する際に、「固定している壁が鉄か粘土か」「固定方法は壁に埋め込んでいるのかL字アングルで固定しているのか」「材料物性は一般的なカタログスペックを使うべきなのか」といったことが無意識に省略されるといったことを表しています。
実験と解析のすり合わせを行う際にはこれら「合わない原因」を影響の強いものから徐々に排除していくことになりますが、その際にこれまで全て既知であった解析条件に、合わせ込みのための未知の条件が発生して通常の解析ができなくなることがあります。そのような場合には、実験等により得られた結果から逆解析という手法を用いて未知の解析条件を推定することが必要になります。
本稿では薄板の4点曲げ試験を例に挙げ、逆解析を用いて実験と解析のすりあわせを実際に行ったプロセスについてご紹介いたします。
逆解析とは
CAEツールを用いた計算の多くは「既知の解析条件によって未知の結果を計算する」というものであり、順解析と呼ばれています。それとは逆に「既知の結果から未知の解析条件を推定する」という流れを逆解析と呼びます。
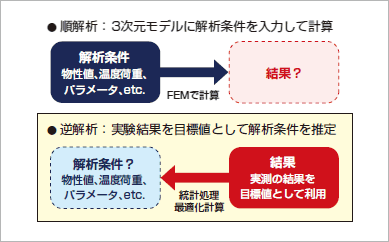 順解析と逆解析の概念図
順解析と逆解析の概念図 逆解析の手法としては、逆定式化法、出力誤差法、最小分散推定法といったものがありますが、本稿では 最適化ソフトOptimus を用いた出力誤差法による逆解析を行います。
出力誤差法は、未知の解析条件を設計変数、実験値と解析結果の誤差を目的関数として、これを最小化する最適化問題を解く事により最適な解析条件を推定する方法であり、Optimusのような最適化ソフトの機能をそのまま利用できるため、他の手法と比較して容易に逆解析を行うことができるという利点を持ちます。
実験と解析の概要
本事例では、弊社で開催している「CAEユニバーシティ FEM実験室ver.1」で実際に測定されたデータを用いており、実験内容は次頁の図のように、両端をクランプ固定したSUSの薄板の2点に荷重をかけ、中央部の変位を観察するというものになります。
これを再現するための初期解析モデルは、端部を固定した対称性考慮の1/4シェルモデルで、幾何学的非線形性の設定を行っています。
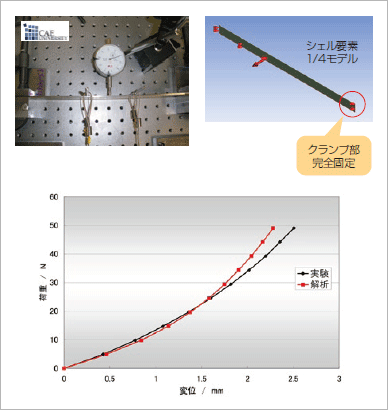 実験モデルと解析モデルの図
実験モデルと解析モデルの図 変位-荷重の結果を比較してみると、変位量が小さいうちは実験と解析の結果はある程度一致していますが、荷重が増加して変位量が大きくなると明らかに両者の挙動が変わっていることがわかります。
また、これは結果のグラフには現れていませんが、以下のような挙動も示していました。
- 実験後におもりをはずしても変位量がゼロに戻らない
- 固定を全てはずすと平板に戻る
次項からはこれらの結果をふまえて逆解析による実験と解析のすり合わせを行います。
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

非線形解析の壁を突破するシミュレーション技術
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない実レベルの振動解析
~Ansys Mechanicalで実現する高度な製品開発~
-
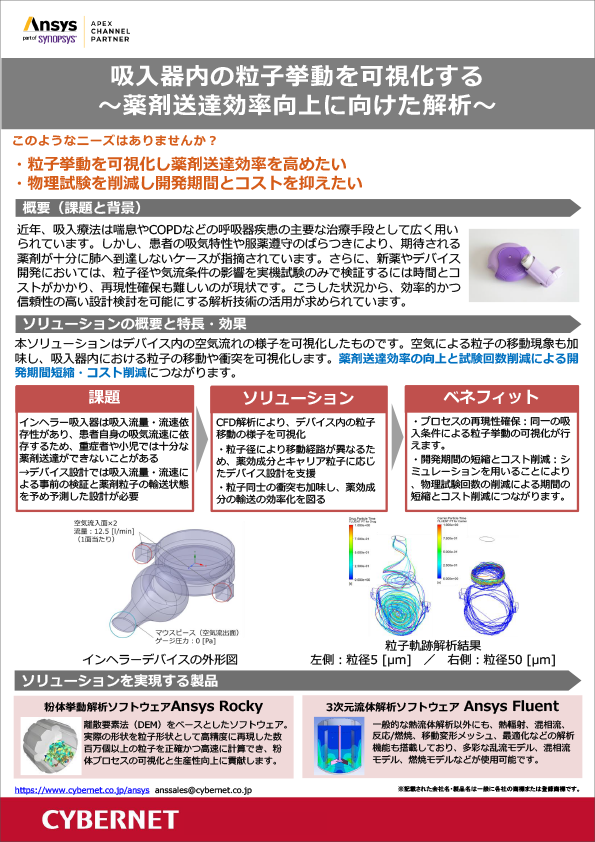
吸入器内の粒子挙動を可視化する
~薬剤送達効率向上に向けた解析~
-

医薬品バイアルの温度挙動解析
~保管環境の影響把握と品質維持に向けた可視化アプローチ~
-

そのFDTD計算、もっと速くできる!Lumerical+GPUでフォトニクス解析に革命を