CAEを学ぶ
FEMを用いた身近なものづくり体験~パスタブリッジ解析検証事例~
~パスタブリッジ解析検証事例~
はじめに
昨今のFEMプログラムは以前と比べてCADとの連携が強化され、操作もより簡便になりつつありますが、それと共に利用者の層が大きく拡大しており、層が広がった分利用者の解析との関わり方も多種多様になっています。
そのような利用者の中には実際のものづくりに関わらない技術者も多く、設計目標が限界に近づく中で、実際の挙動を想像できないまま解析の結果だけを信じて設計を行った結果、不具合品を出してしまうということもあるでしょう。さらに設計サイクルが短期間の場合は、なぜ不具合品になってしまったのかを検証する時間もなく次の設計に進むこともあるでしょう。
実際のものづくりにおける試行錯誤や失敗の経験は強烈であり、これまではそれらの積み重ねが熟練の技術者を育ててきましたが、製品の製造工程が複雑になり、技術者の分業が進む現状を考えると、全ての技術者が実際のものづくりを経験すると言うのも無理な話なのかもしれません。
本稿ではこのような現状をふまえ、身近な物を用いて実現象と解析をすり合わせて試行錯誤や失敗を経験できる例として、さまざまな教育機関でも授業の一環として用いられているパスタブリッジを挙げ、実際に検討した内容などをご紹介いたします。
パスタブリッジとは
パスタブリッジとは、その名のとおりパスタをホットボンドのような速乾性の接着剤を用いて組み上げた橋のことを指しますが、ただ単に橋を作成するだけではなくさまざまな制約条件を設け、それを達成するような橋を実際に作ることが目標となります。
パスタブリッジには技術レベルに応じた制約条件を設定することにより、初級者から上級者まで幅広い技術者の挑戦が可能ですが、本稿では説明用に以下のような少ない制約条件の問題を用意し、2次元の解析と検証を行っています。
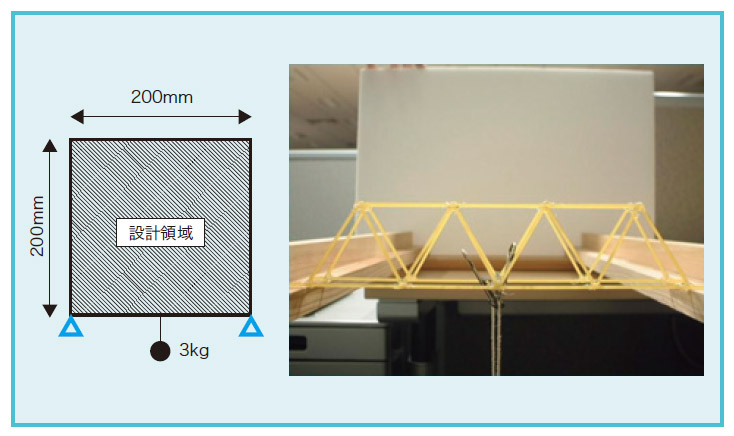
【パスタブリッジ設計・製造の制約条件】
・設計領域の最底辺中央に3kgのおもりを紐で吊るすことができる
・使用するパスタの量をできるだけ少なくする
解析の前準備
さて、これから実際にパスタブリッジをモデル化して解析を実施することになりますが、その前に行う必要のある項目を挙げて検討します。
(a) 基本となる形状の決定
設計初期段階では制約条件による設計領域だけが決まっており、基本形状をどのようにすればよいのか不明な状態のため、まずは位相最適化を行うことでどのような基本形状にすべきかの指針を探ります。
なお、位相最適化は厚肉部品の設計向けの機能であり、パスタブリッジのような骨組み構造向けではないため、その解析結果はあくまでも参考程度としています。
上図は位相最適化の結果ですが、これを参考に今回の基本形状は正三角形の組み合わせモデルとします。
(b) 使用する要素
使用するパスタは単純な円形断面の細長い棒状構造であり、変形は軸方向および曲げが支配的となるため、梁要素でのモデル化が適切であると思われます。面外せん断の影響はほとんど無いと考えられますが、BEAM188はティモシェンコ のビーム理論に基づいており適用範囲が広いため、解析ではこの要素を用いることとします。なお、パスタは断面が円形のため、ワーピングの自由度を考慮する必要はありません。
(c) パスタの材料特性
パスタの材料物性は、「パスタブリッジコンテスト」「ヤング率」といったキーワードでWEBを検索するといくつかヒットしますが、身近な道具で簡単な3点曲げ試験などを行い、大雑把な値を求めるのもいいかもしれません。
また、パスタがどんな荷重によって破壊してしまうのかわからない場合は、軸方向や曲げ方向の破壊荷重を求める試験も併せて行う必要があるかもしれません。
(d) パスタ結合部の影響
本モデルではパスタの結合にホットボンドを用いており、パスタと比べると充分硬いためビーム要素同士を節点共有してモデル化できますが、弱い粘土などで結合する必要がある場合は、結合部の節点を共有せずにカップリングとばねの組み合わせによる結合を行うことで挙動をモデル化する必要があるかもしれません。
(e) 固定と荷重
出来上がったパスタブリッジは台の上に置いて中央部におもりを吊り下げますが、これを解析で表現するにはこの状態を境界条件に置き換える必要があります。
台に置かれている部分は浮き上がらないと仮定すると、固定はUY方向の単純支持で表現できます。また、おもりの部分は力荷重に置き換えることで同じく表現できると思われます。
3kgのおもりの影響を力荷重に変換するには【力】=【質量】×【重力加速度】の式を用いますが、解析に用いる単位系(ton、mm、sec)に当てはめて考えると【力】=3e-3x9800=29.4Nであり、これが今回の荷重値となります。
なお、パスタブリッジ本体は非常に軽く、自重による変形は軽微なものと予測されるため、荷重としての重力は省略できるものと思われます。
(f) パスタブリッジの解析モデル
本モデルは形状、荷重が左右対称であり、静解析の結果も左右対称となることが予想されるため、解析モデルは1/2対称モデルとして作成することが可能です。
なお、力荷重を定義する節点が対称境界面上にあるため、荷重値は半分にする必要があります。
解析結果とその検討
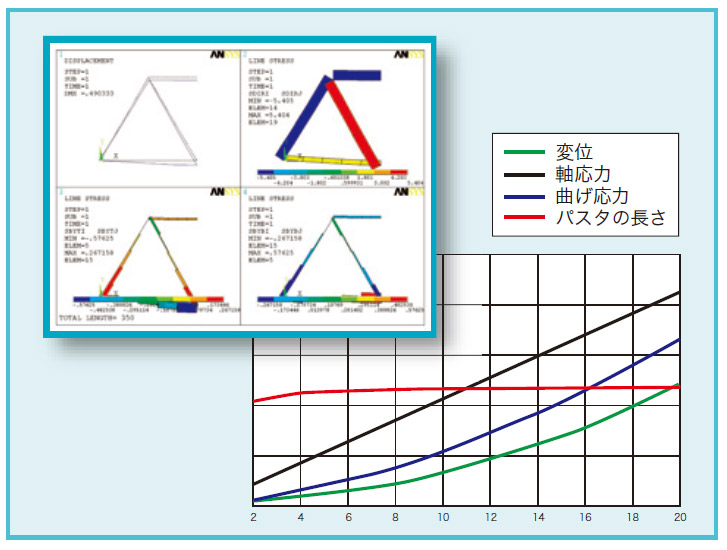
前項の検討を考慮したモデルで正三角形の数を変えて解析を行い、最大の変位、軸応力、曲げ応力、パスタのトータル長さをプロットした図を以下に示します。
この結果を見ると、全ての結果で上向き三角形が2個のモデルの値が最も低く、三角形の数が増えれば増えるほど高くなっている様子が観察できるため、このモデルが最良設計として良いと思われます。
しかしながら、検証のために実際に上向き三角形が2個のモデルを作成しておもりを載せてみると簡単に壊れてしまいました。逆に上向き三角形が8個あるモデルを作成して試験を行うと、3kg以上のおもりを載せても壊れませんでした。これはどういうことでしょうか?位相最適化や静解析の結果が間違っていたのでしょうか?
モデルを見ただけでお気づきになられた方もいらっしゃるかもしれませんが、上向き三角形が2個のモデルは応力が材料の限界に達して壊れたのではなく、実はパスタが座屈することによって壊れていました。
長い梁はオイラーの式で求まる座屈応力が軸方向に与えられると、材料の破壊応力に達していなくても折れ曲がって破壊しやすくなるため、最適な形状を得るためには静解析だけでなく座屈解析も同時に実施して、応力による破壊と座屈による破壊の両方を回避できるモデルを選択する必要があるということになります。
上のグラフは上向き三角形の数と今回負荷する荷重および座屈荷重の関係をプロットしたものですが、これによると上向き三角形が6個のモデルなら座屈しないという結果になります。
ただし、これは線形座屈解析の結果のため、実際の座屈荷重はグラフにプロットされた値よりも小さくなる傾向があり、パスタのように初期不整となりえる材料および形状のばらつきが大きな対象物については解析結果と真の座屈荷重の差がより大きくなります。
よって最終的には絞り込まれた条件を実験によって確認するか、さらに確率論的な解析を実施することにより、最終的な最良モデルを判断することになります。
最後に
ものづくりの経験が豊富な技術者にとって、本稿の解析結果から得られた結論は解析するまでもなく気づく内容であり、実際の業務でも初期の段階で不具合になる可能性の高いモデルはモデル化の候補から除外されるため、精度が高い解析を効率良く行うことができます。また、最良な設計には力学的な問題だけでなく、部品の作りやすさやデザインといったFEMで計算することが難しい要素もたくさん含まれており、それらも含めて総合的な判断を下すにはやはり実際にものづくりを行った経験が大きいと思われます。
まずは身近なものづくり体験!いかがでしょうか?
(CAEのあるものづくり2008年9号掲載)
関連情報
関連する解析事例
MORE関連する資料ダウンロード
MORE-

【全記事】CAEのあるものづくり vol.42
ユーザー様インタビュー記事7件を1冊に集約した保存版
-

誤差との上手なつきあい方 ~流体解析の計算誤差~ (完全保存版)
誤差との上手なつきあい方 前編・後編 を1冊にまとめた保存版 PDF
-

非線形解析の最大強度評価はAnsys LS-DYNAで解決!
~Ansys LS-DYNAで解決!最大荷重評価のボトルネック~
-

事例でご紹介!流体解析分野のエンジニアリングサービス ~解析業務の委託・立ち上げ支援・カスタマイズによる効率化など~
-

はんだ濡れ上がり形状予測解析で電子機器の信頼性向上
~Ansys LS-DYNAで電子機器の信頼性向上に貢献~
-

Ansys ユーザーのための PyAnsys 完全ガイド
Pythonで加速するCAEワークフロー
-

共振回避だけで終わらせない振動解析の進め方を解説(周波数応答・時刻歴まで)
~Ansys Mechanicalで実現する高度な製品開発~
-
吸入器内の粒子挙動を可視化することで薬剤送達効率の向上へ
~薬剤送達効率向上に向けた解析~