分野別の課題
薄膜LiNbO₃位相変調器の解析事例
こんな方におすすめ
解析概要
本事例では、薄膜LiNbO₃(LN)変調器の電気特性解析を行います。まず、Step1としてAnsys Lumerical CHARGEを用いてポッケルス効果による屈折率変化の解析を行います。続いて、Step2としてStep1で解析した屈折率変化をモデルにインポートし、Lumerical FEEMを用いて光学解析を行います。なお、本記事の内容は Thin Film Lithium Niobate Electro-Optic Phase Modulator – Ansys Optics に基づいております。
使用ソフトウェア
Ansys Lumeraical CHARGE
Ansys Lumeraical FEEM
※2023R1.2以降のバージョンが必要です。
解析目的および解析手法
背景と目的
高速・大容量通信や高精度センサへの需要が高まる中、LNの優れた電気光学効果を最大限に活用するには、ポッケルス効果を考慮した解析が不可欠です。しかし、通常のFDTD解析のみではポッケルス効果などの非線形光学効果を考慮した解析は困難です。そのため、光と電気の連成解析が可能なLumerical Multiphysics(CHARGEとFEEM)を使用し、薄膜LN変調器の電気光学特性の解析を行います。
解析対象
解析対象を図1に示します。本事例は2Dシミュレーションとなっています。 SiO2基板上に薄膜LNが配置されており、Ground電極2つとSignal電極1つが配置されています。ただし、解析領域はオレンジ色の線で囲われた領域(Signal電極と一方のGround電極のみ)となっております。
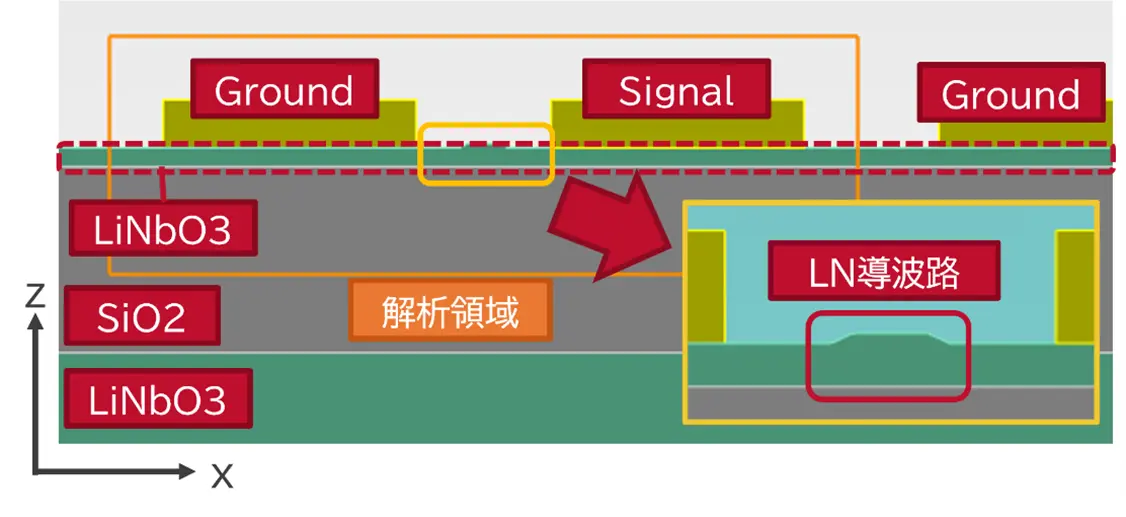
図1 解析モデル
解析手法
以下の2ステップで解析を行います。
(1)ポッケルス効果によるLNの屈折率変化の解析(Lumerical CHARGE)
(2)電気光学特性の解析(Lumerical FEEM)
解析内容
Step1. ポッケルス効果によるLNの屈折率変化の解析
ここでは、電圧印加による薄膜LNの屈折率変化(ポッケルス効果)の解析を行います。解析にはLumerical CHARGEを用います。ポッケルス効果による屈折率変化は式(1)に基づいて計算されます。
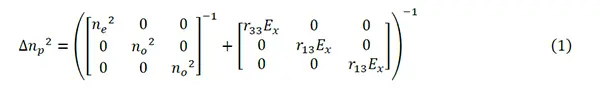
これを各方向成分に展開すると式(2)のようになります。
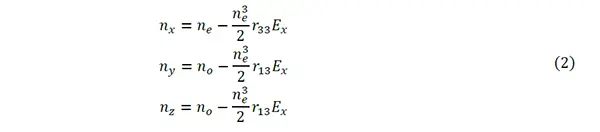
※本事例は2Dシミュレーション(xz平面)であり、Ey=0となります。また、Ex≫EzであるためExによる影響のみを考慮しています。
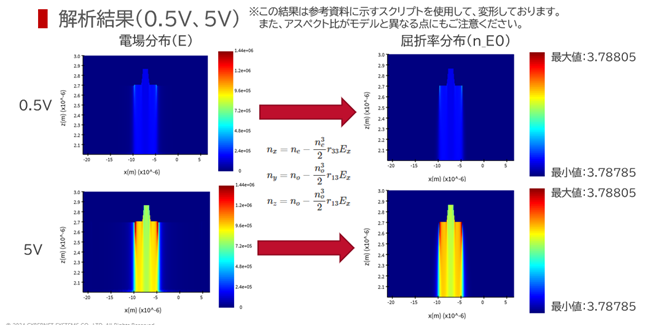
図2に解析結果を示します。電圧を0-5V(0.5V間隔、11ステップ)で変化させ、それぞれの電圧におけるLN導波路の屈折率変化を算出しています。

図2 LN導波路の屈折率変化(0.5V,5V時)
Step2. 電気光学特性解析
次にStep1で計算した屈折率分布をモデルにインポートし、Lumerical FEEMを使用して以下の特性評価を行います。
- 基本モード・実効屈折率の計算
- Lπ・Vπ Lの計算
- 損失の計算
まず、基本モードと実効屈折率の計算についてです。結果を図3に示します。各電圧においてTE偏光成分が95%以上のモードを基本モードとし、そのモードにおける実効屈折率を取得します。この操作をすべての電圧で行うことで実効屈折率を計算します。
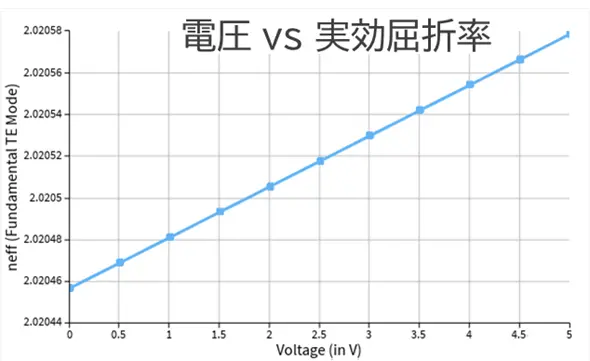
図3 LN導波路の実効屈折率
続いて、Lπ・Vπ Lの計算についてです。結果を図4、5に示します。Lπは式(3)に基づいて導出されます。電圧とLπの関係から印加電圧が大きくなると光の位相がπ変化するために必要な変調器の長さは短くなることがわかります。また、VπLはすべての電圧で約3.2V・cmとなっています。

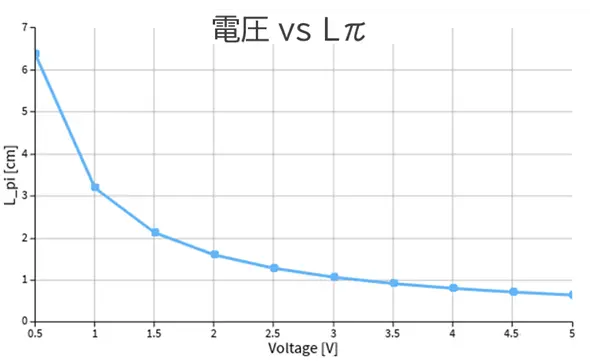
図4 LN変調器のLπ
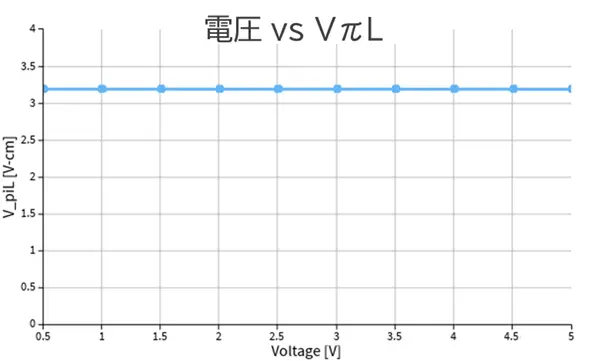
図5 LN変調器のVπL
最後に、LN変調器の損失の計算についてです。結果を図6、7に示します。LN変調器の損失は式(4)により求められます。本モデルの損失は電圧に依存しないことが図6からわかります。一方、5V印加時の基本TEモードを確認するとモードの一部が電極へと侵入し、金属による吸収損失が発生している可能性が考えられます。
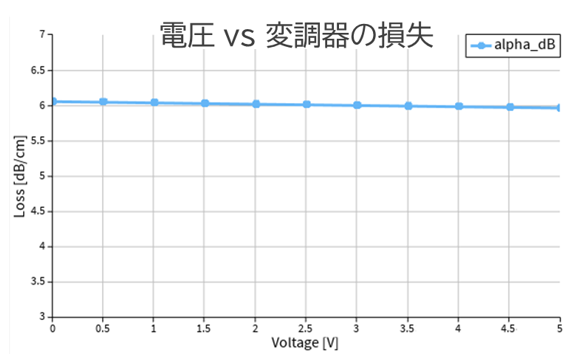
図6 LN変調器の損失
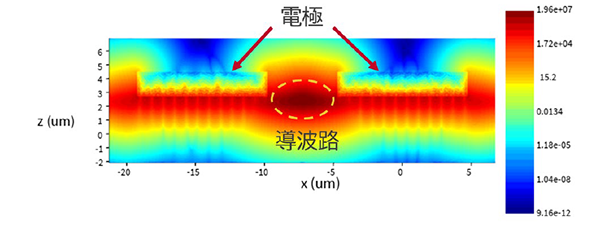
図7 5V時の基本TEモードにおける電場分布(ログスケール)
まとめ
Lumerical Multiphysics(CHARGE+FEEM)を用いた、薄膜LN位相変調器の解析例をご紹介いたしました。CHARGEソルバーとFEEMソルバーを用いることにより、FDTDなどの電磁場解析のみでは困難なポッケルス効果の影響を考慮した薄膜LN位相変調器の電気光学特性の解析を行うことが可能となります。
また、下記ボタンよりダウンロード可能な資料では本モデルを使用して簡単なAC解析を行った結果を記載しております。
※内容の詳細は、下記ボタンより資料ダウンロード頂けます。