資料ダウンロード
はじめての最適化(第1回)

この連載では、いわゆる『最適化』についてこれから勉強される方を対象に、最適化の基礎知識としてアルゴリズムおよび周辺技術について代表例を挙げて、その概要を説明します。
最適化とは
最適化という言葉は現在広く一般的な言葉として使用されていますが、この連載では次のように定義された最適化を扱います。
「最適化とは、関数/プログラム/製造物などを最適な状態に近づけること」
特にCAEを利用した最適化を行う場合は、CAEにより得られる出力値が最小化または最大化される解(入力値)を求めることが目的となります。(目標値への最適化の場合は、目標値との差などを最小化します) このとき、そのような解を探索するための様々なアプローチを総称として最適化と表現する場合や最適化アルゴリズムによる解の探索を最適化と表現する場合があります。
最適化アプローチ
まずここでは最適化アプローチから説明します。一般的な最適化アプローチでは単に最適化アルゴリズムを使用して最適解を探索するだけではなく、事前に実験計画法や応答曲面法を利用することで対象とする最適化問題の特徴を捉えます。そこで得られた情報を元に設計変数の絞り込みや適切な最適化アルゴリズムの選択が行われ、全体として効率的な最適化を行います。
一般的な流れとして次のようなアプローチが考えられます(図1)。まず未知の最適化問題に対してその特徴を把握するため、実験計画法によるサンプリングを行います。続いて、得られたデータから応答曲面モデル(近似式)を作成します。これにより改善したい評価指標にどのような特徴(特性)があるか把握します。次に得られた情報を元に設計変数の絞り込みなどを実施し、適切な最適化アルゴリズムを用いて最適化計算を実施します。ここで得られる最適解はCAEを使った計算の場合、同じ入力値を与えれば原則同じ出力値が得られるようなある意味で理想条件での最適解となります。しかしながら現実においては入力値に対し常にバラツキが発生し、それに伴って出力値にもバラツキが発生します。そこでより現実に近い最適化としてこのようなバラツキを考慮した最適化も行われます。
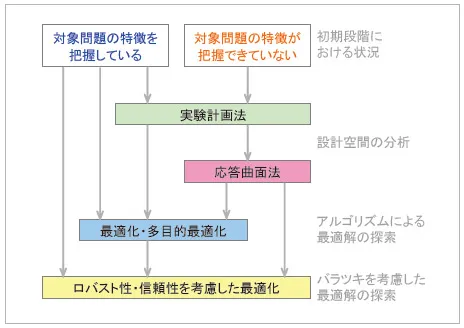
図1 最適化アプローチの例
以上が一般的な最適化アプローチとなり、この全体を指して最適化と表現することがあります。
一方、最適化アルゴリズムを使用した解の探索を指して最適化と表現する場合もありますが、その探索イメージを以下に説明します(図2)。
最適化アルゴリズムによる解の探索では、まず対象となるシステムが必要となります。対象システムは入力値を与えると、それに応じた何らかの出力値を返す仕組みが必要です。例えばCAEや関数、Excelによる計算の仕組みや実測の実験などが考えられます。このようなシステムに対し、最適化アルゴリズムは入力値を与え、システムから出力された応答が最適かどうかを判断し、最適でなければ新たな入力値を与えるという繰り返しを行い、得られる出力値が最適な解となるまで繰り返し計算を行います。
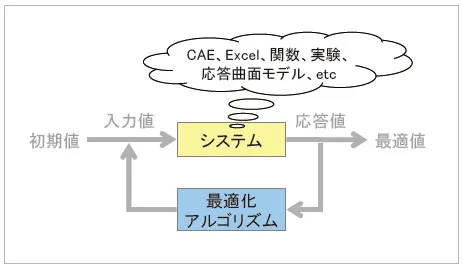
図2 アルゴリズムによる最適化イメージ
最適化問題の定式化
最適化を実施する際、まず行わなければならないのが問題の定式化です。一般に最適化問題は次のように定義されます(図3)。

図3 最適化問題の定式化
ここで目的関数は改善したい評価指標で、通常最小化問題として扱われます。(最大化問題は目的関数にマイナスの符号を付加した最小化問題として扱われます) 制約条件は最適化において満足しなければならない条件、設計変数は目的関数を改善するために調整可能な変数です。簡単な構造解析を例に考えると、質量を目的関数として最小化する際、発生する応力が許容応力以下であるという制約条件を考えます。このとき設計変数としては、製品の寸法や物性値などが扱われることになります。このように定式化した問題において、最適化アルゴリズムが最適解を求めることになります。
従って目的関数、制約条件、設計変数をそれぞれどのように定義するか充分に考慮する必要があります。さらにCAEを使った最適化の場合は、対象モデルの解析に1回あたりどの程度の計算時間を要するかということも重要になります。前述のとおり最適化では繰り返しの計算を必要とするため、解析時間によってどれだけ最適化計算を実施できるかが左右されます。充分な計算回数を確保できれば解ける問題でも現実的には時間的な制約があり、最適解に達するまで計算できないといったことが起こりえます。
基本用語
ここでは最適化に関して一般的によく使用される基本的な用語について説明します(図4)。
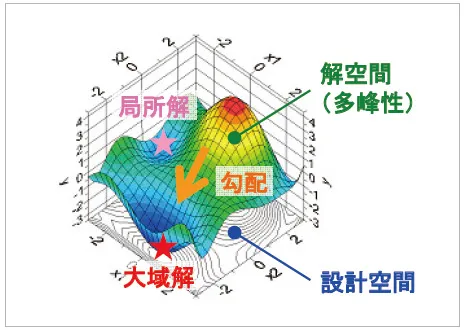
図4 基本的な用語
設計空間 : 設計変数の組み合わせにより作られる集合を意味し、最適解を探索する空間です。多数の設計変数が定義される場合、設計空間は多次元の空間となるため、一般に次元が増えるほど解の探索は難しくなります。
解空間 : 設計空間上に作り出される目的関数の曲面です。特に解空間に山や谷となる領域が1つ存在する場合は単峰性の問題と呼ばれ、複数存在する場合は多峰性の問題と呼ばれます。多峰性が強いほど、極値となる点が複数存在するため、一般に難しい問題となります。
勾配 : 解空間における任意の点の曲面の傾きを意味します。(目的関数を設計変数でそれぞれ偏微分した情報)局所的最適解(局所解) : 解空間においてある近傍領域で良好な解。
大域的最適解(大域解) : 定義された設計空間において最も良好な解。(局所最適解の中で最良の解)
最適化問題の分類
定義した最適化問題は様々な基準により分類することができます。最適化問題にはそれぞれ特徴があり、それに応じて適切な最適化アルゴリズムを選択する必要があります。ここでは最適化アルゴリズムを選択するにあたり、どのような最適化問題の分類があるか、いくつかの例を挙げます。
*続きはダウンロードしてお読みください。


