世界最先端の記号・数値演算エンジンを搭載
高度な計算、可視化、データ分析、アルゴリズム作成… あらゆる数学的なニーズに対応
STEM コンピューティング・プラットフォーム『Maple』は、1980年にカナダ・ウォータールー大学で生まれた数式処理技術をコアテクノロジーとして持つ科学・技術・工学・数学に関する統合的計算環境です。数値計算を行うだけでなく、実行可能な技術文書作成や計算アプリ開発によって、様々なシーンでの活用を可能にします。
Maple の詳細はこちら >>
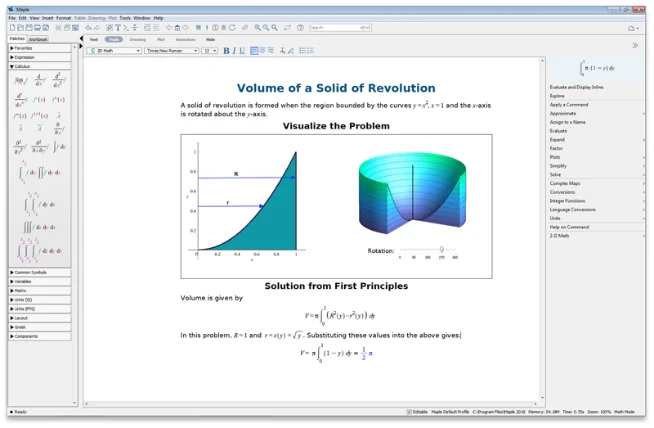
より深い解析と高度なソルバにより、
数学的な問題を解決
単一環境で、計算ツール、
数学に対応したスクリプト、
内蔵の解析アプリケーションにアクセス可能
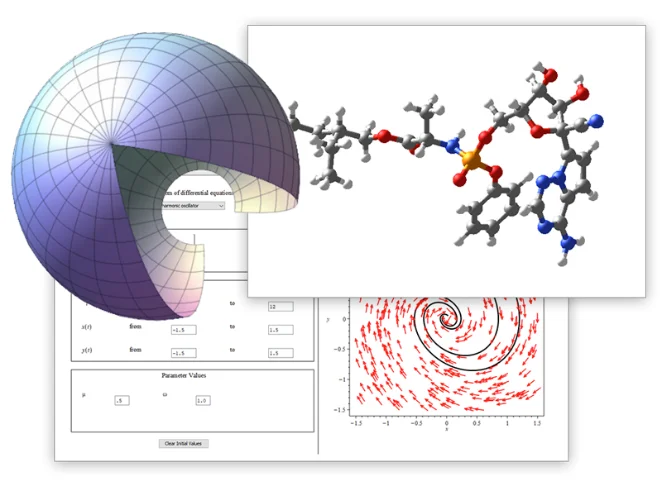

単一環境で、計算ツール、
数学に対応したスクリプト、
内蔵の解析アプリケーションにアクセス可能
Mapleの数学エンジンを利用した1Dシステムレベルモデリング&シミュレーションツール
開発期間の短縮、コスト削減、マシン性能の問題診断を可能に
次世代の1D CAE ソフトウェア『MapleSim』は、Maplesoft のコアテクノロジーである数式処理技術とモデリング言語 Modelica の融合を軸に、電気、機械、熱、流体、信号等、さまざまなドメインにまたがる統合的なモデリングとシミュレーションによるシステム開発環境を提供します。
MapleSim の詳細はこちら >>
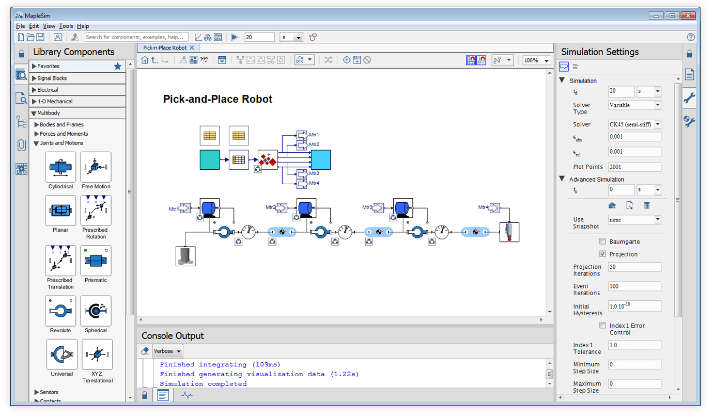
設計概念とパフォーマンスの結果を
最適化して探求
マシン(製造装置)や製品の
マルチドメイン・システムモデルを作成
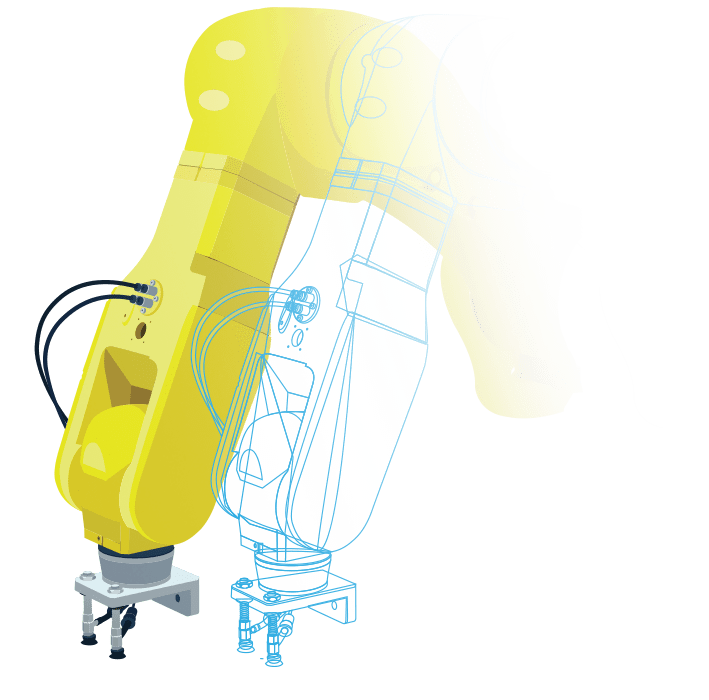

マシン(製造装置)や製品の
マルチドメイン・システムモデルを作成

バーチャルコミッショニングや
デジタルツインのアプリケーションのための
環境をシミュレート
計算を流れるように
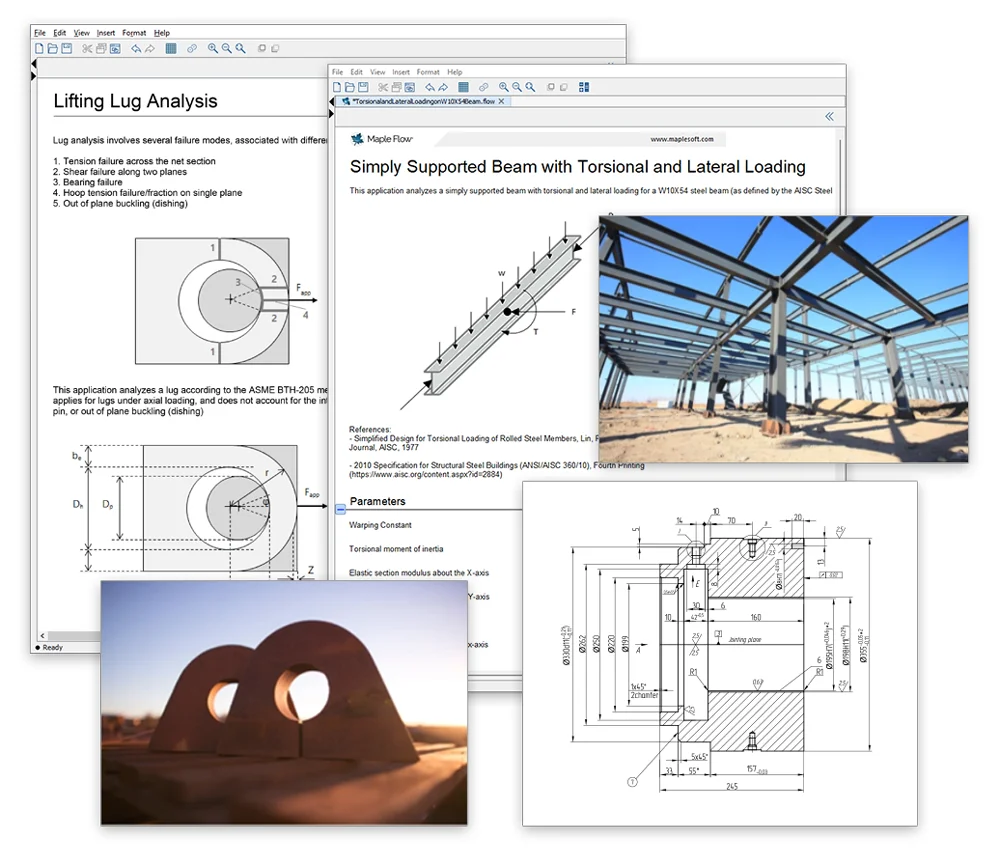
紙のような自由度の高いスクラッチパッド型インターフェース
Maple Flow には高速なソルバ、ビルトイン単位のトラッキング、柔軟なプロットなど、技術者が計算に必要な機能が備わっております。ツール上での作業とは思えないような自由度の高いインターフェースで数学の演算、テキスト、画像、グラフなどを好きな場所に配置し、計算/記録することができます。
Maple Flow の詳細はこちら >>
無料トライアル、製品に関するお問い合わせはお気軽にご連絡ください。