Multiscale.Simによる非線形マルチスケール解析 (5)

目次

PSO最適化アルゴリズムと材料物性値同定

Multiscale.Simでは、異方性クリープの材料モデルとしてHillポテンシャルにもとづく構成則を採用しております。今回は紙面の都合上、材料モデルの詳細については割愛して、材料物性値の同定手法について紹介します。

材料物性値の同定は最適化解析を利用して行います。最適化を図る目的関数（Φ）には、材料試験の応答と材料モデルの応答との誤差を定量化したものを与えます。式で表現すると

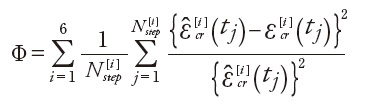
となります。ここでiは6方向の材料試験を表す数値、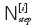は方向試験のサンプリング点数で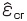と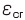はそれぞれサンプリング点jの時刻における、材料試験と材料モデルが示す相当クリープひずみです。この汎関数の最小化問題を最適化することで物性値同定が実現します。解析の大まかな流れを図5に示しました。

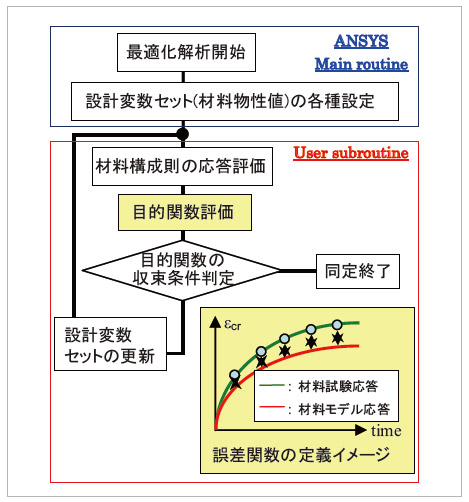
図5　最適化解析による材料定数同定の流れ

設計変数の更新ルールには、先進的な最適化アルゴルズムである粒子群最適化（PSO）を採用しております※5 。PSOは数ある確率論的な最適化アルゴリズムの中でも優れた収束性を示すことで知られており、その有用性から広い分野に応用されることが期待されております※6 。群知能を基本とした社会的行動モデルであり、複数の個体の情報を群全体で共有しながら、探索領域が絞られていきますが、定式化を次に簡単にまとめます。

各々の個体が設計空間の中で移動する速度ベクトルvは現在のイタレーションkの情報をもとに次のように更新されます。

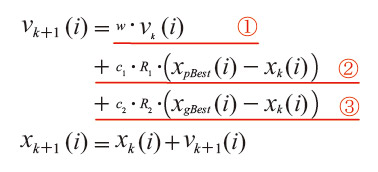
ここでwは探索個体が持つ慣性力に関する重み係数、xkは探索個体iの現在の位置ベクトルで、添え字pbestとgbestはそれぞれ、各探索個体が探索履歴の中で得た最良点位置、探索個体群全体の中の最良点位置を表します。C1とC2は任意の係数、R1とR2は乱数値です。本定式化を図示すると図6のようになります。図中の数値①～③は、前述した速度ベクトルの更新式の第1項から第3項の成分を表しております。探索個体に慣性の影響を考慮していることや、履歴のbest情報に乱数による重みをつけることで、多峰性の応答曲面を持つ問題に対しても局所最適解が避けられるような対策がとられています。

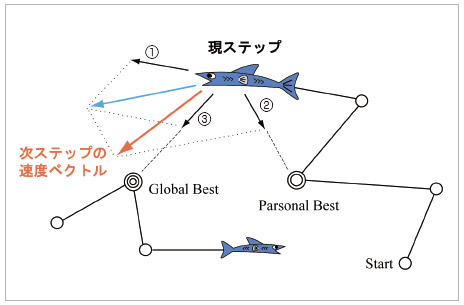
図6　PSOにおける探索個体移動規則の概念図

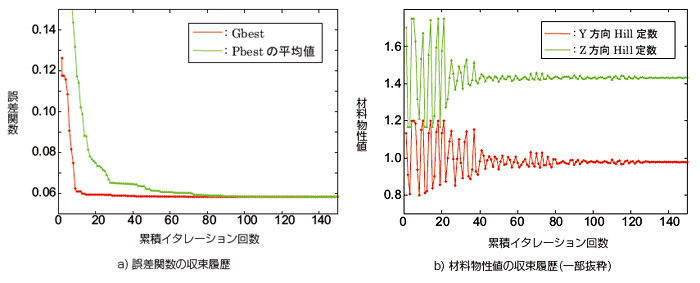
さて、前節で得られたクリープ数値材料試験のデータに対して、PSO最適化によるカーブフィットを実行した結果を図3に実線で示しました。単軸方向のみを代表して表示しておりますが、非常に良好な同定精度が得られている様子が確認できます。図7には収束履歴を確認した結果を示しています。イタレーションの増加とともに探索個体が最適値に向かって収束している様子が確認できます。

図7　PSO最適化解析の収束履歴

おわりに

マルチスケールに関連する学会や勉強会等にて、均質化法という言葉は将来的に論文等の紙面では、存在しなくなる可能性を示唆する話を拝聴することがあります。これは決して理論が衰退するという意味合いではなく、FEMの解析では「あえて言うまでもなく」均質化法を併用していることが暗黙の了解となるとの推測が元になってなります。複合材料の将来性を期待しての言葉でもありますが、本ツールが採用しているアプローチの有用性を物語ってもいるものと期待しております。マルチスケール解析の取り組みが、複合材料を用いた解析に携わる皆様の課題を解決する糸口となることを心より願っております。