関連情報
数値材料試験による異方性非線形材料特性の算出 〜Hillの異方性塑性パラメーターの同定〜
日東紡績株式会社 グラスファイバー開発研究所
平山 紀夫
東北大学大学院工学研究科
寺田賢二郎 准教授
1.はじめに
現在の汎用の有限要素法プログラムは、様々な材料非線形問題に対応できるように非常に多くの非線形材料モデルが用意されています。
特にAnsysに代表されるようなプリ・ポスト処理を統合したCAEツールでは、材料試験の結果から非線形材料定数を同定するフィッティングツールまで用意されています。そして最近では、材料の非線形特性に異方性がある場合でも対応ができるように、異方性の材料非線形構成則が標準で組み込まれています。例えばAnsysでは、様々な非線形材料モデルとHill型の異方性モデルを組み合わせることによって複雑な異方性材料の非線形挙動を模擬できます。具体的には、
(1)等方硬化をともなう速度非依存の異方性塑性
(2)移動硬化をともなう速度非依存の異方性塑性
(3)複合硬化をともなう速度非依存の異方性塑性
(4)等方硬化をともなう速度依存の異方性塑性 (異方性粘塑性)
(5)移動硬化をともなう異方性クリープと異方性塑性等
非常に多種多様な材料モデルの組み合わせが可能です。
しかしながら、Hillの異方性パラメーターを実際に材料試験から算出するためには、全部で6方向の材料試験を行う必要があります。そして、材料試験から得られた応力-ひずみデータからHillの異方性パラメーターを算出しなくてはなりません。実際に6方向の材料試験を実行して異方性パラメーターの算出を行うためには、異方性材料の試験片の準備・作成から行わなくてはならず多くの時間と労力が必要となります。一般的には、異方性材料の材料試験片は作成すること自体が難しく、さらに材料試験も等方性材料の時のように簡単に行うことができません。
著者らはこのような異方性の非線形材料特性の算出には、非線形均質化解析をベースにした数値材料試験が有用だと考えています[1]〜[3]。
本解説では、プラスチックを炭素繊維で強化した一方向強化複合材料の異方性塑性を例にして、Ansysを利用した非線形均質化解析による数値材料試験を用いたHillの異方性パラメーターの算出について解説します。
2.数値材料試験によるHillの異方性パラメーターの算出
2.1. Hillの異方性パラメーター
最初に、Hillの異方性パラメーターについて簡単に紹介しておきます。Hillのモデルでは異方性材料の降伏を扱うために、次のような降伏関数を使用します。

ここで、Hill応力 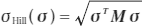 を次式で定義します。
を次式で定義します。
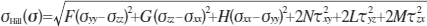
この降伏関数における は、累積塑性ひずみαを硬化パラメーターとする硬化関数です。また、行列Mは材料の直交異方性を仮定して次のように定義します。
は、累積塑性ひずみαを硬化パラメーターとする硬化関数です。また、行列Mは材料の直交異方性を仮定して次のように定義します。
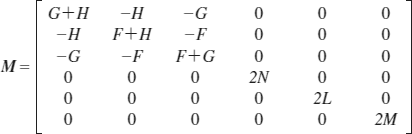
ここで、F 〜 NがHillの異方性係数と呼ばれるもので、各軸方向の材料試験から得られる降伏応力の比Rxx ,Ryy ,Rzz ,Rxy ,Ryz ,Rzxと次式で関係付けられています。
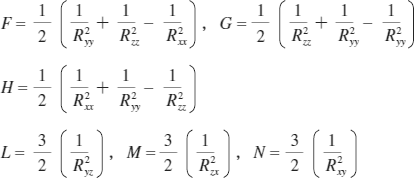
Ansysで入力しなくてはならないHillの異方性パラメーターは、F〜Nの異方性係数ではなく、降伏応力の比Rxx 〜 Rzxになることに注意してください。数値材料試験でも、この降伏応力の比Rxx 〜 Rzxを算出することになります。以後、各軸方向の材料試験から得られるこれらの比Rxx 〜 RzxをHillの異方性パラメーターと呼ぶことにします。
なお、これらのパラメーターは正規化した値でよいため、本稿ではRxxを1とおいて他のRij値をRxx対する比で表現することにします。
(Ansysで入力する場合には、どのRij値を1とおいてもかまいません)
2.2 数値材料モデル
数値材料試験によるHillの異方性パラメーターの算出手順を説明するために、今後、航空機や自動車分野で採用が期待される熱可塑性プラスチックを炭素繊維で強化した一方向強化複合材料の数値材料モデルを取り上げます。この一方向強化複合材料の数値供試体(ユニットセルモデル)を図1に示し、線形の均質化解析で算出した異方性の材料物性値を表1に示します。表1から明らかなように、ここで例示した一方向強化複合材料は著しい異方性を持っています。また、繊維軸方向以外には弾性体である炭素繊維の物性がそれほど寄与しないと考えられるため、繊維軸方向以外にはマトリックスの非線形性が複合材料の異方性の非線形材料特性に大きく反映されることが予測できます。マトリックスである熱可塑性プラスチックは、ポリアミド樹脂(ナイロン6)を想定しています。材料試験から得られたポリアミド樹脂のS-S曲線を図2に示します。この図からわかるように、このポリアミド樹脂は比較的微小なひずみ領域から非線形性が現われています。
このような熱可塑性プラスチックの非線形性を塑性現象として取り扱ってよいかどうかは、より厳密な検討が必要ですが、今回は塑性モデルとして取り扱い多直線等方硬化 (MISO) オプションで近似することにしました。
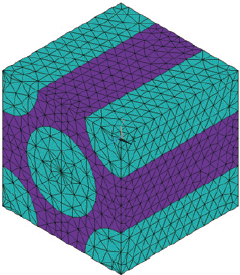
図1 一方向強化複合材料の数値材料モデル
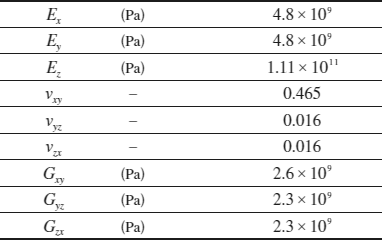
表1 一方向強化複合材料の材料物性値
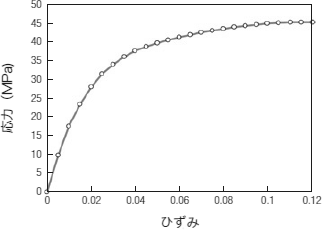
図2 ポリアミド樹脂のS-S 曲線
2.3 数値材料試験とHillの異方性パラメーターの算出手順
均質化法を使用した数値材料試験の手順に関しては、文献[1]〜[3]に詳しく記載されていますので、そちらをご一読ください。ここでは、6方向の数値材料試験の結果から得られた材料データから、Hillの異方性パラメーターを具体的に算出する手順について解説します。
はじめに、ij = xx ,yy ,zz ,xy ,yz ,zx 方向のそれぞれの6方向の数値材料試験を行います。今回は、一方向強化複合材料のミクロモデルにトータルで3%のひずみを適切な分割数で与えて6方向の弾塑性解析を行いました。Hillの異方性パラメーターの定義に従えば、この6方向の弾塑性解析結果から、[ ij ]の各方向一軸状態での降伏応力
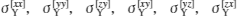
を求め、 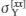 で正規化したHillパラメーターRxx 〜 Rzxを次式で算出すれば良いことになります。
で正規化したHillパラメーターRxx 〜 Rzxを次式で算出すれば良いことになります。
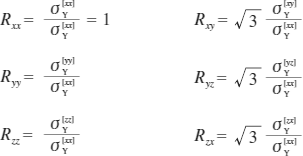
しかしながら、上式でHillパラメーターを算出するためには、各軸方向の解析結果から降伏したかどうかの判定を行わなくてはなりません。そのために、例えば降伏を累積相当塑性ひずみの有無で判定し、降伏直前の2ステップおよび降伏直後の2ステップの応力とひずみで直線を作成してその交点を降伏点とする方法が考えられます。しかし、このような方法でHillパラメーターを算出しますと、ミクロモデルの要素分割等でHillパラメーターが大きく異なるようなことが発生して好ましくありません。そこで、ここでは次のような方法でHillパラメーターを算出することにします。
- まず、6方向の数値材料試験で得られるひずみはトータルひずみのため、弾性ひずみの寄与を除去する必要があります。そこで、次式から塑性ひずみを計算します。
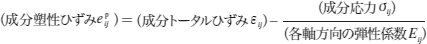
- 次に、仮の値としてHillパラメーターRxx ,Ryy ,Rzz ,Rxy ,Ryz ,Rzxをすべて1とします。
- そして、1.で算出した成分応力
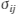 と成分塑性ひずみ
と成分塑性ひずみ 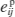 を使用して、次式から[ ij ]の各方向一軸状態でのHillの等価応力
を使用して、次式から[ ij ]の各方向一軸状態でのHillの等価応力 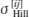 とHillの蓄積等価塑性ひずみ
とHillの蓄積等価塑性ひずみ 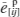 を次式で計算します。
を次式で計算します。

- 最後に、上式から計算した各荷重ケースでのHillの等価応力とHillの蓄積等価塑性ひずみの曲線が一本の曲線に重なるようにHillパラメーターRxx 〜 Rzxを変化させながら繰り返し計算を行い決定します。
以上の手順に従って、図1の一方向強化複合材料のHillパラメーターRxx 〜 Rzxを決定したときの各軸方向でのHillの等価応力とHillの蓄積等価塑性ひずみの曲線を図3に示します。この例ではHillの蓄積等価塑性ひずみが0.5%の時に全ての曲線が一致するようにHillパラメーターを決定しました。繊維軸方向(z軸方向)の曲線が他の曲線と比較して大きくずれていますが、そもそも今回のような一方向強化複合材料では、繊維方向にはほとんど塑性変形しないためRzzは無限大かあるいは非常に大きな値になります。今回のケースのように、特定の方向には塑性変形しない一方向強化複合材料のようなモデルでは、その方向はHillの等価応力とHillの蓄積等価塑性ひずみの曲線群から削除しても構いません(今回はあえて削除していません)。
以上の手順により算出したHillパラメーターを表2に示します。
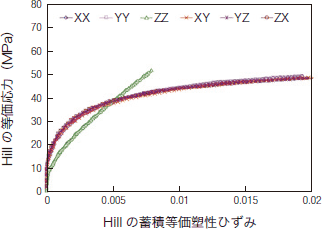
図3 Hillの等価応力とHillの蓄積等価塑性ひずみの曲線
3.算出したHillパラメーターの検証
表2に示した各軸方向の材料試験から算出されたHillパラメーターRxx 〜 Rzxの値と、[xx]方向のHillの等価応力とHillの蓄積等価塑性ひずみの曲線を用いて、ユニットセルを均質異方性体として数値材料試験を行い、前章での一方向強化複合材料の各軸方向の材料試験が再現できるかを検証しました。もし、前章の手順で算出したHillパラメーターが一方向強化複合材料の異方性を表現できているとすれば、そのパラメーターを使用して同じ荷重条件で材料試験を行った異方性均質体の応力-ひずみ曲線は、前章での一方向強化複合材料のそれと一致するはずです。検証結果を図4に示します。この図から明らかなように、一方向材料の数値材料試験と算出したHillパラメーターでモデル化した異方性均質体での解析結果は全ての荷重方向で良い一致を示しています。若干、せん断ひずみの大きな領域で差がみられますが、現実的には炭素繊維で強化した一方向強化複合材料の破断ひずみは2%を超えることはないため、実用的なレベルでは大きな誤差ではありません。
4.おわりに
本解説では、Ansysを利用した非線形均質化解析による数値材料試験を行うことで、Hill型の異方性塑性材料の非線形材料物性を算出する手順を示しました。Ansysでは、様々な非線形材料モデルとHill型の異方性モデルを組み合わせることによって複雑な異方性材料の非線形挙動を模擬できるため、この記事で解説した方法の適用範囲は非常に広いはずです。ここで紹介したような数値材料試験では、実際の材料試験からは得ることのできなかった多くの情報を得ることが可能で、従来では見過ごしていた材料挙動を観察することもできます。本解説が多くの読者の方々の解析業務に少しでも参考になる点があれば幸いです。

表2 材料試験から算出されたHill パラメーター
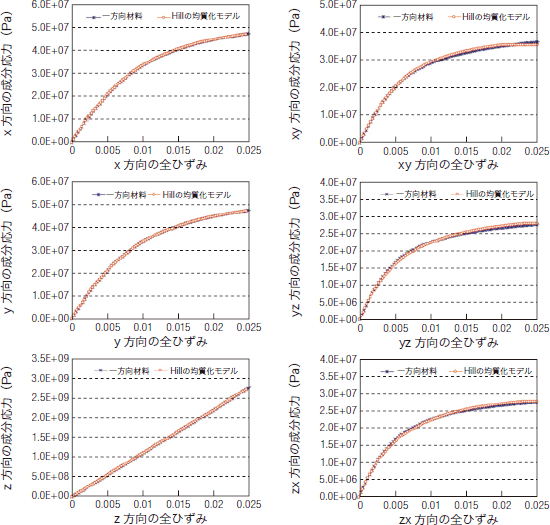
図4 一方向強化複合材料の検証結果
[1]寺田賢二郎・菊池昇:均質化法入門,丸善(2003)
[2]寺田賢二郎:マルチスケールCAE 〜数値材料試験のススメ〜,CAEのあるものづくり,サイバネットシステム,Vol.5 ,p.9-10 ,2006
[3]平山紀夫:Ansysを利用したマルチスケールCAE 〜 Ansysを利用した数値材料試験〜,CAEのあるものづくり,サイバネットシステム,Vol.6 ,p.11-15 ,2007
CAEのあるものづくりニュースは、年2回(春・秋)発行されています。Ansysシリーズ、Optimusを始めとした各種メカニカルCAE製品の最新情報だけでなく、お客様の解析事例紹介やインタビューなどの現場の声や、また技術トピックなどを充実させた読み応えのある内容としてご好評いただいております。
ご希望の方は、資料ダウンロードページよりご請求下さい。



