資料ダウンロード
CFDシミュレーションにおける乱流の課題
Application Brief

2017年9月
目次
2次元のはく離
CFDエンジニアの主要な課題の1つに、流れのはく離の正確な予測があります。ほぼすべての設計で、はく離領域はデバイス効率の損失に関連するため、解消または最小化することが望まれています。ディフューザは多くの流体設計における非常に傑出した機械的要素です。ディフューザは内部流れで異なる直径の流路を接続するために必要であり、ほぼすべての産業部門および用途で使用されています。ディフューザ設計の目標は、可能な限り小型化しつつ、同時にその壁面からのはく離を避けるか最小化することです。コンパクトな設計では結果として二次側の開口角が大きくなり、それがはく離を起こしやすくするため、最適化の問題が発生します。図1はディフューザ内流れの計算結果を示しています。流れは左側から入り、狭い流入口部分を通り、ディフューザを通過して右側から出ていきます。この実験は日本の慶応義塾大学と、スタンフォード大学で行われました[1]。二次側の開口角が10°でレイノルズ数(Re)が20,000の非対称のジオメトリを含みます。この実験では、傾斜した壁から流れがはく離しています。SST乱流モデルとk-εモデルの比較から、k-εモデルでははく離気泡が完全に失われていることがわかります。同じ図の速度分布は、SSTモデルが予測するはく離流れが、実験結果と良好に一致することを示しています。
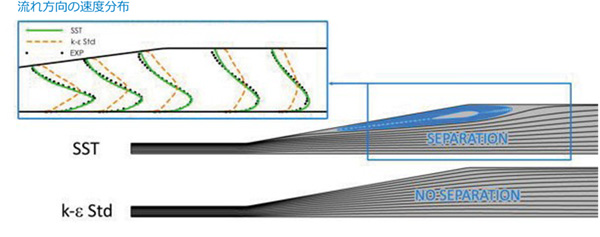
図1 : Obiディフューザ内の流れ。
上 : SSTモデルでのシミュレーション。下 : K-εモデルでのシミュレーション。
このような流れでk-εモデルを実行すると、ディフューザ設計の過度に楽観的な結果をエンジニアに提供することになります。シミュレーション結果と相反し、実際のディフューザははるかに大きな圧力損失を示します。壁面上に大きくて非定常な力がかかることで、非定常な渦の離脱までも引き起こす可能性があります。
3次元のはく離
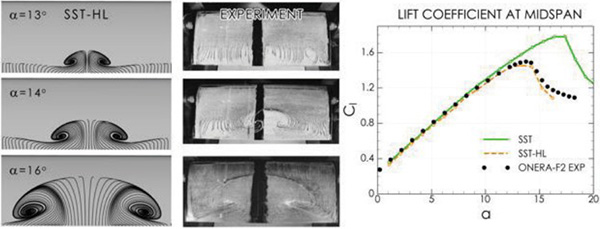
図 2 : さまざまな迎え角αによる風洞内の翼型。
左 : 最適化されたSSTモデルで計算された流れトポロジー。
中央 : 該当する実験による油の流れの画像。
右 :揚力係数Clと迎え角αの比較。
図2に流れのはく離のより複雑な例を示します。迎え角αを変更した時の風洞内の翼型の表面流れを示します。実験の設定[2]が基本的に2次元であるのにかかわらず、流れは3次元構造で表されます。この現象はキャプチャが難しく、3次元モード(オレンジ色の破線による曲線)のSST-HL(HLはHighLift(高揚力)の略)モデルの拡張バージョンのみで再現できます…