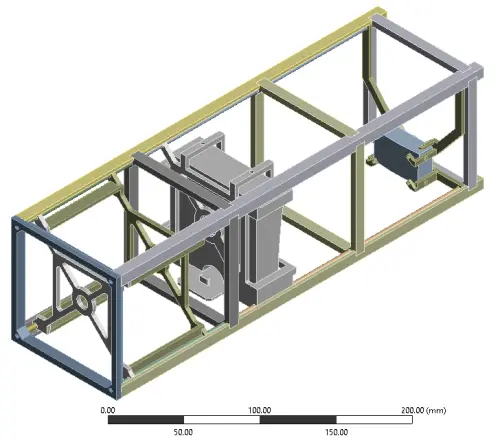
CAEを学ぶ
弾塑性材料モデルの基礎(第2回)
佐賀大学 大学院工学系研究科 機械システム工学専攻 只野 裕一 様
弾塑性材料モデルの基礎(第2回)の概要

弾塑性材料モデルの基礎 第1~4回 完全保存版 PDF を "無料" 公開中!

弾塑性材料モデルの基礎 完全保存版 PDF サンプル
これさえ読めば”弾塑性材料モデルの基礎”がわかる
全4回のシリーズとなっております「弾塑性材料モデルの基礎」について、4回分の解析講座を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
ページ数:24 ページ
ファイル形式: PDF
佐賀大学 大学院工学系研究科
機械システム工学専攻 只野 裕一 様 著
【完全保存版 PDF 目次】
|
1. はじめに 2. 弾塑性モデルの概要 3. 弾塑性モデルを理解するための 予備知識 4. 降伏関数 |
5.ひずみ硬化則 6. 弾塑性構成式の基礎 7. おわりに |
4 降伏関数
4.1 降伏関数とは
弾塑性変形を記述するにあたって重要となる3つの因子のうち、今回は降伏関数について解説します。降伏関数とは、材料がいつ降伏するかを記述する数学モデルです。弾塑性変形における応力・ひずみ線図(第1 回の図1をご参照ください)を見てもわかるように、延性材料では応力が降伏応力に達すると降伏を生じます。その後、塑性変形の進行と共に降伏は維持されていると考えるため、この最初に降伏することを特に初期降伏と呼ぶこともあります。このように、材料の降伏は応力によって支配されていると考えることできます。
材料が降伏する、すなわち塑性変形を開始する条件を降伏条件と呼びます。降伏条件を具体的な関数で表現したものが降伏関数です。降伏が応力によって支配されていることから、降伏関数は応力の関数となります。また、降伏関数に応力以外の状態変数を加えることも可能です。例えば、温度や変形速度を降伏関数に含めることで、これらの降伏への影響を考慮することができます。
降伏関数![]() をすると、一般に
をすると、一般に![]() は次式を満たすスカラー値関数として定義されます。
は次式を満たすスカラー値関数として定義されます。

すなわち、材料が弾性状態にあるときは常に負で、降伏するときにゼロなるような関数![]() を定義することになります。弾性状態で
を定義することになります。弾性状態で![]() 、降伏の瞬間(初期降伏)で
、降伏の瞬間(初期降伏)で![]() となることから、その後塑性変形が進行する間は
となることから、その後塑性変形が進行する間は![]() となるように思われるかも知れません。実際にそのような定義は可能であり、塑性変形の速度依存性を考慮する場合にはそのような定式化を行う場合もあるのですが、一般的な弾塑性モデルでは
となるように思われるかも知れません。実際にそのような定義は可能であり、塑性変形の速度依存性を考慮する場合にはそのような定式化を行う場合もあるのですが、一般的な弾塑性モデルでは![]() となる状態は考えません。それでは塑性変形進行中はどう考えるのかというと、常に
となる状態は考えません。それでは塑性変形進行中はどう考えるのかというと、常に![]() となるようにうまく降伏関数を定義するのです。これは、降伏応力が定数ではなく塑性変形の進行と共に変化すると考えることで解決できます。この塑性変形に伴う降伏応力の変化については、次回のひずみ硬化則で取り上げることになります。
となるようにうまく降伏関数を定義するのです。これは、降伏応力が定数ではなく塑性変形の進行と共に変化すると考えることで解決できます。この塑性変形に伴う降伏応力の変化については、次回のひずみ硬化則で取り上げることになります。
それでは、降伏関数の具体形について見ていきましょう。現在までに数多くの降伏関数が提案されていますが、本稿では古典的かつ重要な2 つの降伏関数であるTrescaとMisesの降伏関数について学び、降伏関数の考え方の基本を解説します。特にMisesの降伏関数は、多くの汎用FEMコードにおいて標準的な弾塑性モデルに採用されている降伏関数であり、またその中で用いられるMises応力は多くのポストプロセッサでデフォルトの出力となっている量です。本稿を通じて、Mises応力に対する理解も深めて頂きたいと思います。
4.2 1次元の降伏関数
まずは1 次元問題における降伏関数を考えてみましょう。これは、単軸引張・圧縮状態を考えているということになります。一般に降伏点を評価するための最も簡単な材料試験は単軸引張試験ですので、単軸引張試験において材料が降伏する応力を降伏応力![]() としましょう。実際の材料試験においては、明確な降伏点が観測される材料と、そうでない材料(弾性変形から塑性変形への遷移が連続的であり、降伏点が不明瞭な材料)があります。後者の場合、例えば塑性ひずみがある値となるときの応力をもって、降伏応力とみなす場合があります(よく使われるのは塑性ひずみが0.2%となるときの応力で、これを0.2%耐力と呼びます)。
としましょう。実際の材料試験においては、明確な降伏点が観測される材料と、そうでない材料(弾性変形から塑性変形への遷移が連続的であり、降伏点が不明瞭な材料)があります。後者の場合、例えば塑性ひずみがある値となるときの応力をもって、降伏応力とみなす場合があります(よく使われるのは塑性ひずみが0.2%となるときの応力で、これを0.2%耐力と呼びます)。
降伏応力![]() が与えられているとき、軸方向の応力を
が与えられているとき、軸方向の応力を![]() とすれば、降伏関数はつぎのように表現することができます。
とすれば、降伏関数はつぎのように表現することができます。

この降伏関数に、弾性状態の応力![]() を代入すれば、
を代入すれば、
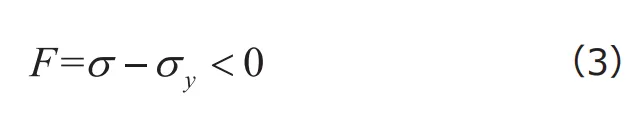
となりますから、弾性状態では降伏関数は常に![]() となります。応力
となります。応力![]() が降伏応力
が降伏応力![]() に達すると材料は降伏しますが、この状態を降伏関数に代入すれば、
に達すると材料は降伏しますが、この状態を降伏関数に代入すれば、

となり、確かに式(1)の条件を満たしていることがわかります。初期降伏後に塑性変形が進行すると、一般に応力![]() は上昇していきます。式(4)が塑性変形中は常に満たされるようにするためには、前述のようにひずみ硬化則を導入することで、降伏応力
は上昇していきます。式(4)が塑性変形中は常に満たされるようにするためには、前述のようにひずみ硬化則を導入することで、降伏応力![]() が塑性変形と共に変化するよう定義します。
が塑性変形と共に変化するよう定義します。
このように1次元問題であれば、式(1)を満たす降伏関数は容易に定義することができます。しかし、2次元、3次元の問題となると、ちょっとやっかいです。応力はテンソルであり3次元であれば6 つの独立成分を持ちますが、あらゆる応力状態に対して降伏応力を実験的に測定することは不可能です(複数の応力成分を考えると、応力の加え方の組み合わせは無限に存在します)。また![]() はスカラー値関数ですから、応力テンソルからスカラー値関数を定義する必要があります。そこで、応力テンソルをなんらかのスカラー量(これを相当応力と呼びます)に変換し、スカラー値関数である降伏関数
はスカラー値関数ですから、応力テンソルからスカラー値関数を定義する必要があります。そこで、応力テンソルをなんらかのスカラー量(これを相当応力と呼びます)に変換し、スカラー値関数である降伏関数![]() を定義することを考えてみましょう。
を定義することを考えてみましょう。
4.3 Trescaの降伏関数
延性金属材料の降伏はせん断応力によって引き起こされることが、古くから実験的に知られています。ある点における応力テンソルの成分は座標系によって値を変えますが、垂直応力やせん断応力が最大となる座標系が存在すること、その最大値を主応力、主せん断応力と呼ぶことを前回学びました。このことから、主せん断応力はある点におけるせん断応力の大きさを特徴付ける量と考えることができます。3 次元状態では主せん断応力も3 つ存在するのですが、その中でも最大のもの(最大せん断応力)が基準値に達すると材料が降伏すると考えたのがTrescaです。最大せん断応力![]() は、最大主応力と最小主応力の差の
は、最大主応力と最小主応力の差の![]() として求められます。すなわち、Trescaの降伏条件は
として求められます。すなわち、Trescaの降伏条件は
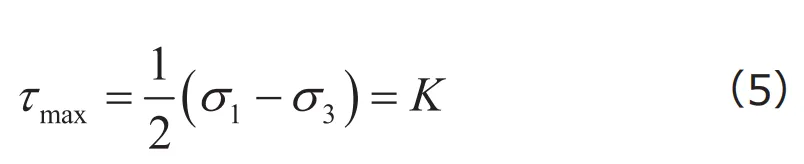
と表現することができます。![]() 、
、![]() は
は![]() となるよう定義したときの主応力、
となるよう定義したときの主応力、![]() は基準となるせん断応力です。Trescaの降伏条件は、最大せん断応力によって材料が降伏するというアイデアであることから、最大せん断応力説とも呼ばれています。
は基準となるせん断応力です。Trescaの降伏条件は、最大せん断応力によって材料が降伏するというアイデアであることから、最大せん断応力説とも呼ばれています。
![]() の値は、具体的にはどのように決めればよいでしょうか。最大せん断応力のみが作用するような実験ができれば、そこから同定することも可能ですが、これは一般には難しい実験です。そこで、単軸引張試験の結果から
の値は、具体的にはどのように決めればよいでしょうか。最大せん断応力のみが作用するような実験ができれば、そこから同定することも可能ですが、これは一般には難しい実験です。そこで、単軸引張試験の結果から![]() を同定することを考えてみましょう。単軸引張試験で材料が降伏したとき、軸方向応力は降伏応力
を同定することを考えてみましょう。単軸引張試験で材料が降伏したとき、軸方向応力は降伏応力![]() 、その他の応力成分は全てゼロとなります。ですから、このとき主応力は
、その他の応力成分は全てゼロとなります。ですから、このとき主応力は![]() となります。この条件を式(5)に代入すれば、つぎの関係式を得ます。
となります。この条件を式(5)に代入すれば、つぎの関係式を得ます。
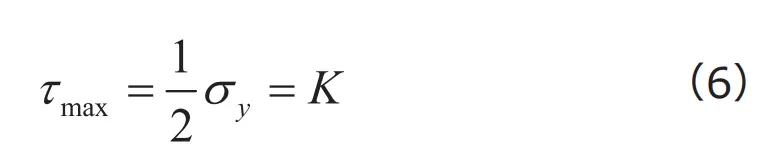
このことから、単軸引張における降伏応力を用いて、![]() と表せることがわかります。この
と表せることがわかります。この![]() は、単軸引張に限らず、任意の応力状態に対して同じ値を用いることができます。ですから、単軸引張試験で降伏応力を同定しその値を
は、単軸引張に限らず、任意の応力状態に対して同じ値を用いることができます。ですから、単軸引張試験で降伏応力を同定しその値を![]() すれば、Trescaの降伏条件に用いる基準応力が求められるのです。これより、
すれば、Trescaの降伏条件に用いる基準応力が求められるのです。これより、
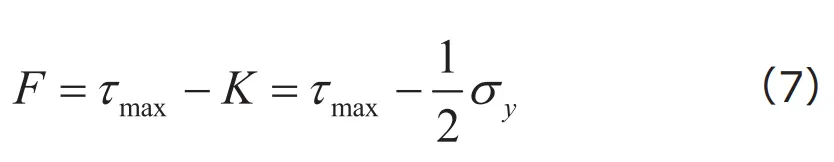
がTrescaの降伏関数として得られます。3次元の任意の応力状態に対して、単軸引張試験における降伏応力のみから降伏関数を定義することができています。これにより、現実的な材料試験から3次元に一般化された降伏関数を得ることができました。もしくは、![]() ここで と定義すれば、
ここで と定義すれば、

というTrescaの降伏関数の別表現も得られます。
4.4 Misesの降伏関数
Trescaの降伏条件では、最大せん断応力によって降伏が支配されていると考えました。これに対して、せん断ひずみによるひずみエネルギーが基準値に達すると材料が降伏すると考えるのが、von Misesの降伏条件、もしくは単にMisesの降伏条件と呼ばれる降伏条件です。Misesの降伏関数の導出に先立って、偏差応力テンソルの主不変量を定義しておきます。第1 回に解説した偏差応力テンソルも応力テンソルの一種ですから、主不変量を求めることができます。偏差応力テンソルの主不変量を特に![]() とすれば、
とすれば、
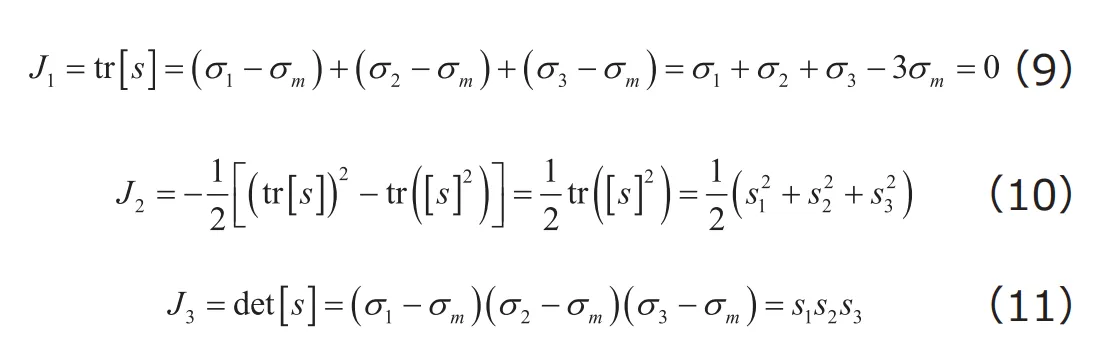
となります。ここで、は![]() 偏差応力テンソルに対する主応力、
偏差応力テンソルに対する主応力、![]() は平均応力です。上式で
は平均応力です。上式で![]() と
と![]() は応力テンソルの主不変量と同じ定義ですが、
は応力テンソルの主不変量と同じ定義ですが、 ![]() は応力テンソルの第2不変量と符号が異なります。これは、
は応力テンソルの第2不変量と符号が異なります。これは、 ![]() の符号が常に正になるように定義するための辻褄合わせと考えてください(符号を反転させただけですから、不変量としての本質は変わりません)。なお、第1不変量
の符号が常に正になるように定義するための辻褄合わせと考えてください(符号を反転させただけですから、不変量としての本質は変わりません)。なお、第1不変量![]() は必ずゼロとなります。これは、応力テンソルの第1不変量は平均応力に対応するものであり、偏差応力テンソルは応力テンソルから平均応力の影響を取り除いたものであることに対応します。
は必ずゼロとなります。これは、応力テンソルの第1不変量は平均応力に対応するものであり、偏差応力テンソルは応力テンソルから平均応力の影響を取り除いたものであることに対応します。
それでは、Misesの降伏条件と降伏関数を具体的に導いてみましょう。ある方向のせん断応力![]() のみが作用しているとき、 によるせん断ひずみエネルギー
のみが作用しているとき、 によるせん断ひずみエネルギー![]() は、対応するせん断ひずみを
は、対応するせん断ひずみを![]() 、せん断弾性係数を
、せん断弾性係数を![]() とすれば、次式で求められます。
とすれば、次式で求められます。
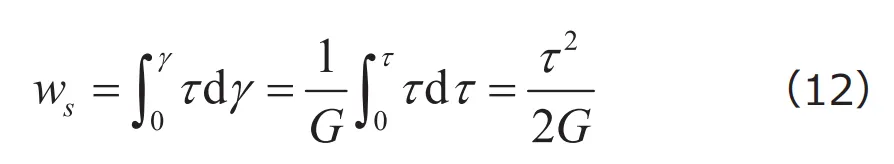
これを用いて、せん断応力が基準値![]() に達したときのひずみエネルギー
に達したときのひずみエネルギー![]() は、
は、

と求めることができます。つぎに3次元的な応力状態において、せん断ひずみによって生じるひずみエネルギー![]() は次式で表されます。
は次式で表されます。
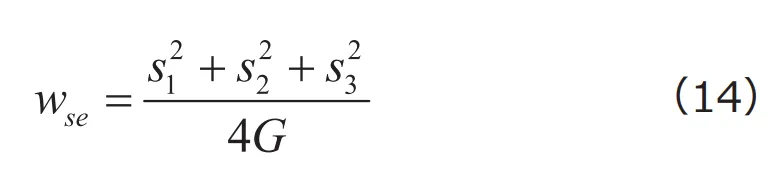
ここで、式(14)のせん断ひずみエネルギーが式(13)で求めたひずみエネルギーと一致する、すなわち![]() となる条件を考えてみましょう。式(13)と式(14)のそれぞれ右辺が等しいとすれば、
となる条件を考えてみましょう。式(13)と式(14)のそれぞれ右辺が等しいとすれば、
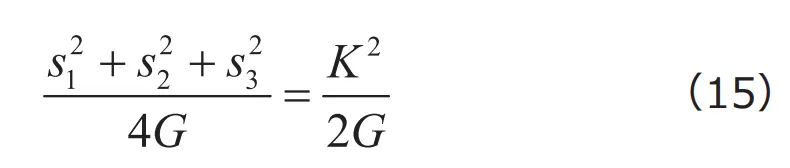
となり、これを変形すれば
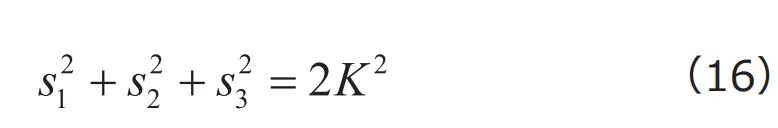
が得られます。ここで式(10)より![]() であることを用いれば、
であることを用いれば、

すなわち、偏差応力の第2不変量が![]() となるとき材料が降伏するという条件式が得られます。もしくは、定義より
となるとき材料が降伏するという条件式が得られます。もしくは、定義より![]() であることから、
であることから、

と表すこともできます。これがMisesの降伏条件となります。せん断ひずみエネルギーによって降伏を生じると考えることから、これを最大せん断エネルギー説とも呼びます。
式(18)より、Misesの降伏関数がつぎのように与えられます。

Trescaの降伏条件と同じように、単軸引張における降伏応力![]() から
から![]() の値を同定することを考えてみましょう。単軸引張で材料が降伏したときの主応力は
の値を同定することを考えてみましょう。単軸引張で材料が降伏したときの主応力は![]() ですから、これに対する偏差応力の主応力は
ですから、これに対する偏差応力の主応力は![]() となります。これに対して偏差応力の第2不変量を求めると
となります。これに対して偏差応力の第2不変量を求めると
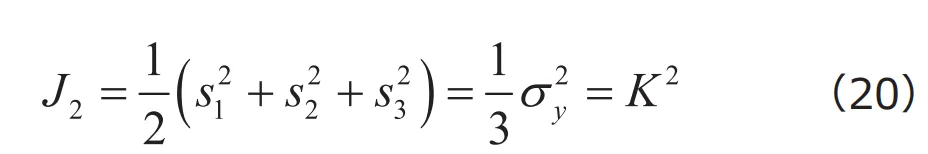
となり、 ![]() という関係を得ることができます。ここで
という関係を得ることができます。ここで

という量を新たに定義しましょう。この![]() をMisesの相当応力、もしくは単にMises応力と呼びます。すると
をMisesの相当応力、もしくは単にMises応力と呼びます。すると![]() となりますから、式(20)をつぎのように書き換えることができます。
となりますから、式(20)をつぎのように書き換えることができます。
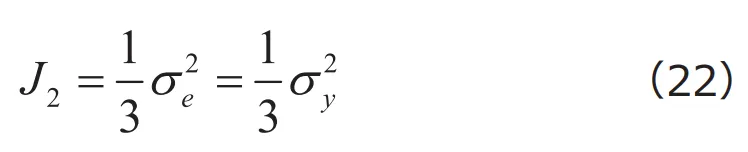
![]() であることから、Misesの降伏条件の別表現として次式を得ます。
であることから、Misesの降伏条件の別表現として次式を得ます。

これを降伏関数として表せば、
![]()
となります。すなわち、Mises応力と単軸引張における降伏応力![]() が等しくなるときに材料が降伏する、という関係が得られるのです。これは大変使い勝手のよい式です。なぜなら、任意の応力状態に対してMises応力を求めたとき、これを単軸引張における降伏応力
が等しくなるときに材料が降伏する、という関係が得られるのです。これは大変使い勝手のよい式です。なぜなら、任意の応力状態に対してMises応力を求めたとき、これを単軸引張における降伏応力![]() と直接比較することで降伏の判定ができるからです。このようにMises応力は延性材料の応力評価にとても便利な量であり、これが多くの汎用ソフトウェアのポスト処理でデフォルトの出力となっている理由です。
と直接比較することで降伏の判定ができるからです。このようにMises応力は延性材料の応力評価にとても便利な量であり、これが多くの汎用ソフトウェアのポスト処理でデフォルトの出力となっている理由です。
ただし、Mises応力も万能ではありません。Mises応力はスカラーであることから、方向の情報は一切含まれません。また定義よりMises応力は常に非負となり、これは引張、圧縮を区別する情報も含んでいないことを意味します。結果として、Mises応力は負荷方向に依存する降伏(異方性降伏)や、引張と圧縮で異なる降伏挙動を示す材料の評価には、必ずしも適切ではありません。また、脆性的な材料にはMisesの降伏条件は一般に当てはまりません(脆性材料の場合、弾性限界や破断の予測には主応力などを用います)。しかし、これらの点に注意を払って適切に扱えば、Mises応力は非常に活躍の場の多い量ですから、その物理的意味と使い方をしっかりマスターしてください。
なお、偏差応力の第2不変量![]() は、偏差応力の主応力のほかに、偏差応力テンソルの成分、主応力、応力テンソルの成分のいずれからも求めることができます。
は、偏差応力の主応力のほかに、偏差応力テンソルの成分、主応力、応力テンソルの成分のいずれからも求めることができます。
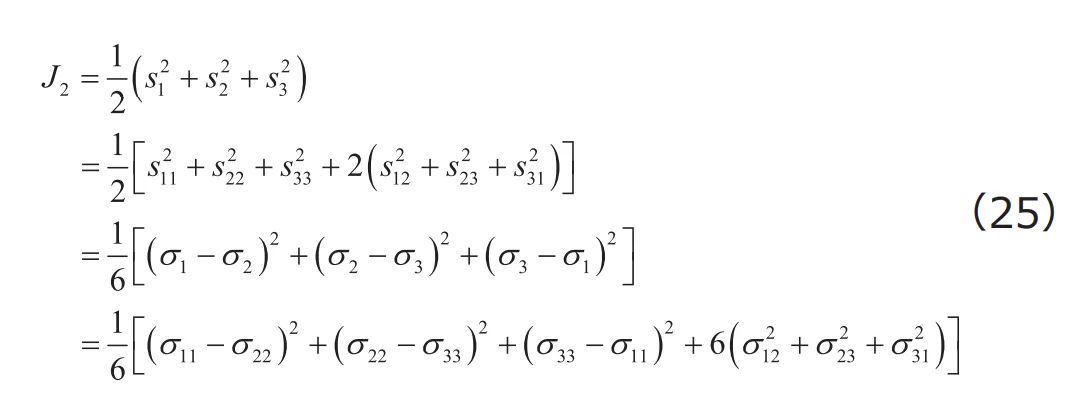
もちろん、どの式からも同じ値が求められますから、計算の上で使い勝手のよい式を使って構いません。
4.5 Misesの降伏関数の別解釈
ここで、Misesの降伏関数について、別の視点からの解釈を紹介します。古くから知られている実験事実として、多くの延性金属材料の降伏は以下の2 つの仮定をほぼ満たすことが知られています。
仮定1: 降伏は平均応力に依存しない
仮定2: 単軸応力状態において降伏は引張と圧縮のいずれでも絶対値が同じ応力で生じる
もちろん、これを満たさない材料も多数存在するのですが、ここではこの2つの仮定を踏まえた降伏関数がどのように記述できるかを考えてみましょう。第1回で解説したよう
に、応力テンソルを構成式に導入する際には、不変量を用いることで座標系に依存しない材料モデルを構築することができます。ここでは、主不変量を用いた降伏関数を考えることにしましょう。
仮定1 より、降伏関数は平均応力の影響を含まないはずですから、応力テンソルの第1 不変量(これは平均応力に対応することを思い出しましょう)は降伏関数に含まれるべきではありません。もしくは、前節で導入した偏差応力テンソルの主不変量を用いても、本質は変わりません(偏差応力テンソルには、平均応力の影響が含まれません)。そこで、仮定1 を満たすために偏差応力の主不変量、![]() 、
、![]() を用いることにしましょう。
を用いることにしましょう。
つぎに仮定2を考えます。応力の絶対値が同じ単軸引張と単軸圧縮では、主応力はそれぞれ
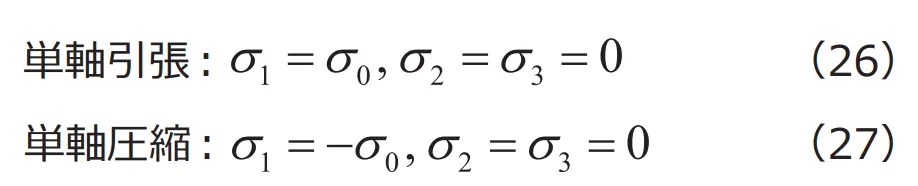
と表すことができます(ただし![]() )。これらに対して、 をそれぞれ
)。これらに対して、 をそれぞれ![]() 、
、![]() 求めてみましょう。
求めてみましょう。
、という形が考えられます。すなわち、
これより ![]() となることがわかります。第2不変量は引張と圧縮で同じ値となりますが、第3不変量は符号が反転しています。仮定2は引張と圧縮で降伏は(絶対値が)同じ応力で起こるとしていますが、これを自然に表せるのは第2不変量
となることがわかります。第2不変量は引張と圧縮で同じ値となりますが、第3不変量は符号が反転しています。仮定2は引張と圧縮で降伏は(絶対値が)同じ応力で起こるとしていますが、これを自然に表せるのは第2不変量![]() ということになります。
ということになります。
以上より、偏差応力テンソルの第2不変量![]() だけを用いれば、2つの仮定を自然に満たす降伏関数が構築できそうです。
だけを用いれば、2つの仮定を自然に満たす降伏関数が構築できそうです。 ![]() を含む降伏関数で最も簡単な形式として、
を含む降伏関数で最も簡単な形式として、![]() がある基準値に達したときに降伏する、という形が考えられます。すなわち、
がある基準値に達したときに降伏する、という形が考えられます。すなわち、

となります。ここで右辺を![]() の2乗としているのは、
の2乗としているのは、![]() が応力の2乗の次元を持つ量となるためです。式(30)は、式(17)に示したMisesの降伏条件そのものです。前節と同様にすれば、ここから式(19)や式(24)のMisesの降伏関数も導かれます。すなわちMisesの降伏条件とは、降伏は平均応力に依存しない、単軸応力状態において降伏は引張と圧縮のいずれでも絶対値が同じ応力で生じる、という2つの仮定を満足する、最も単純な降伏関数の形式と解釈することができます。
が応力の2乗の次元を持つ量となるためです。式(30)は、式(17)に示したMisesの降伏条件そのものです。前節と同様にすれば、ここから式(19)や式(24)のMisesの降伏関数も導かれます。すなわちMisesの降伏条件とは、降伏は平均応力に依存しない、単軸応力状態において降伏は引張と圧縮のいずれでも絶対値が同じ応力で生じる、という2つの仮定を満足する、最も単純な降伏関数の形式と解釈することができます。
4.6 降伏曲面
つぎに、降伏関数を幾何学的に理解する方法として、降伏曲面について解説します。降伏曲面とは、応力空間に降伏関数を満たす点(![]() となる点)をプロットして得られる曲面です。つまり、応力が降伏曲面上に存在するとき、材料が降伏すると解釈できます。ところで、降伏関数は応力テンソルの関数ですが、応力テンソルは一般に独立な6成分を持つため、応力空間は6次元となってしまいます。我々は6次元の空間を直接認識することはできません。そこで応力テンソルの主応力を求め、主応力空間で降伏曲面を考えます。これならば、3次元空間で降伏曲面を捉えることができます。
となる点)をプロットして得られる曲面です。つまり、応力が降伏曲面上に存在するとき、材料が降伏すると解釈できます。ところで、降伏関数は応力テンソルの関数ですが、応力テンソルは一般に独立な6成分を持つため、応力空間は6次元となってしまいます。我々は6次元の空間を直接認識することはできません。そこで応力テンソルの主応力を求め、主応力空間で降伏曲面を考えます。これならば、3次元空間で降伏曲面を捉えることができます。
主応力空間に描いたMisesの降伏曲面を、図1に示します。Misesの降伏曲面は、![]() を中心軸とする半径
を中心軸とする半径![]() の円筒の表面となります。ただし、この曲面に上下底面は存在しません。これは、
の円筒の表面となります。ただし、この曲面に上下底面は存在しません。これは、![]() を保って応力を与える限り、どれだけ高い応力を与えても材料が降伏しないことを意味します。
を保って応力を与える限り、どれだけ高い応力を与えても材料が降伏しないことを意味します。 ![]() を満たす応力状態というのは、平均応力だけが加わる(せん断応力が一切作用しない)状態を意味しており、Misesの降伏条件は平均応力だけでは満たされることがないことに対応しています。
を満たす応力状態というのは、平均応力だけが加わる(せん断応力が一切作用しない)状態を意味しており、Misesの降伏条件は平均応力だけでは満たされることがないことに対応しています。
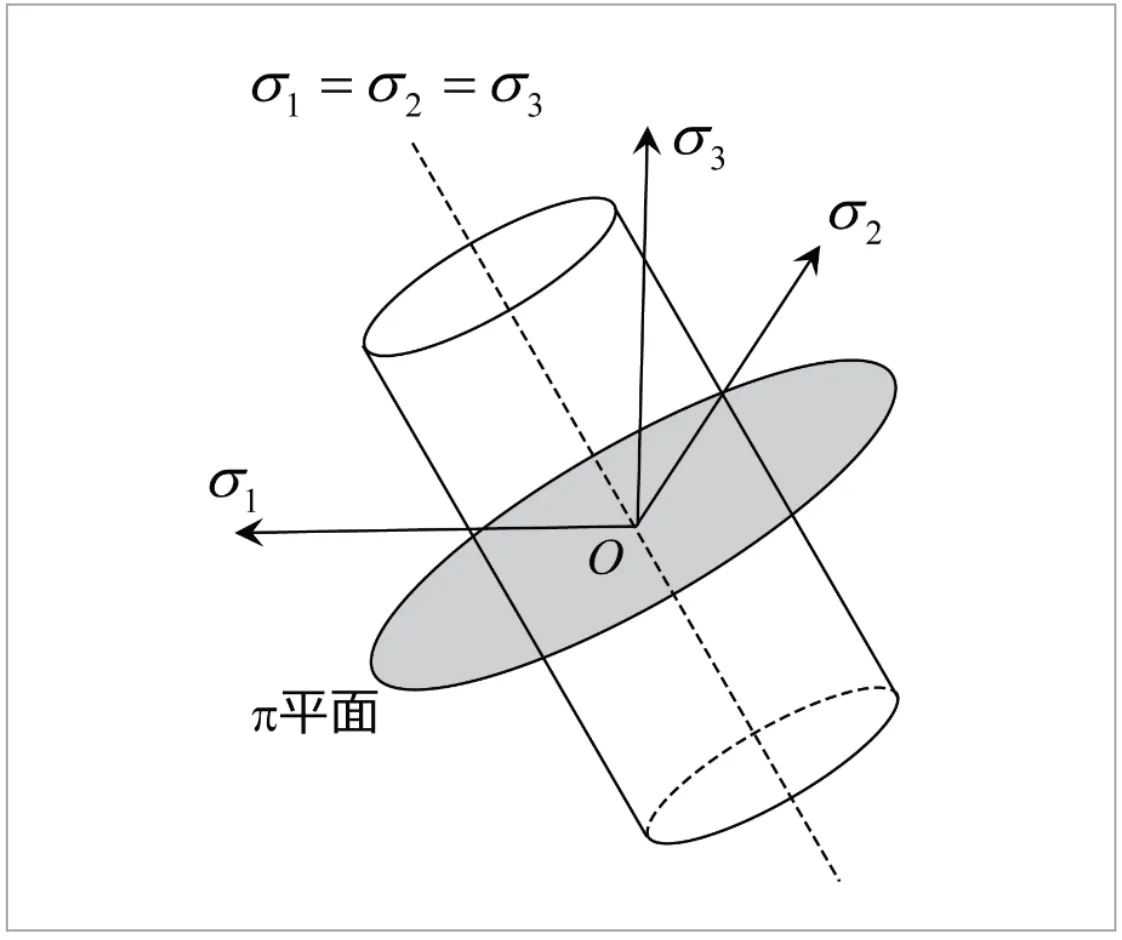
図1 主応力空間におけるMisesの降伏曲面
つぎに、![]() に直交し原点
に直交し原点![]() を通る平面における降伏曲面の断面を見てみましょう。このような平面を
を通る平面における降伏曲面の断面を見てみましょう。このような平面を![]() 平面と呼びます。
平面と呼びます。 ![]() 平面上のTrescaおよびMisesの降伏曲面 を図2に示します。Misesの降伏曲面が真円になるのに対し、 Trescaの降伏曲面はこれに内接する正六角形になります(なお、主応力空間にTrescaの降伏曲面を描くと、図1の円筒に内接する正六角柱の表面となります)。
平面上のTrescaおよびMisesの降伏曲面 を図2に示します。Misesの降伏曲面が真円になるのに対し、 Trescaの降伏曲面はこれに内接する正六角形になります(なお、主応力空間にTrescaの降伏曲面を描くと、図1の円筒に内接する正六角柱の表面となります)。
さらに、応力状態を平面応力に限定すると主応力は2つとなりますから(![]() )、2次元平面上に降伏曲面を得ることができます。これを図3に示します。これは3次元主応力空間における降伏曲面について、
)、2次元平面上に降伏曲面を得ることができます。これを図3に示します。これは3次元主応力空間における降伏曲面について、![]() となる平面における断面を描いたものになります。Misesの降伏曲面は楕 円、Trescaの降伏曲面はこれに内接する六角形(正六角形で はありません)となります。板材の塑性加工などでは、変形を通じて平面応力と見なせる場合も多く、平面応力に特化した降伏関数も提案されています。このため、平面応力状態に対する降伏曲面を目にする機会は少なくありません。
となる平面における断面を描いたものになります。Misesの降伏曲面は楕 円、Trescaの降伏曲面はこれに内接する六角形(正六角形で はありません)となります。板材の塑性加工などでは、変形を通じて平面応力と見なせる場合も多く、平面応力に特化した降伏関数も提案されています。このため、平面応力状態に対する降伏曲面を目にする機会は少なくありません。
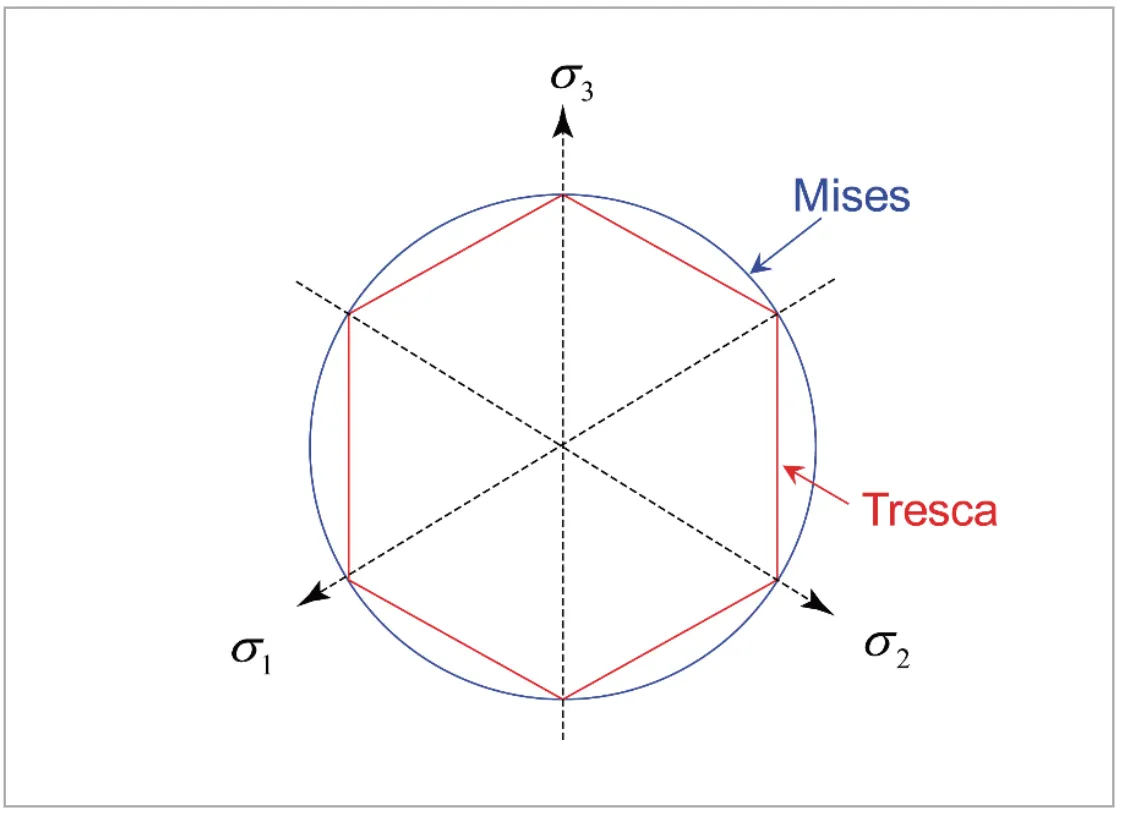
図2 平面におけるTrescaとMisesの降伏曲面
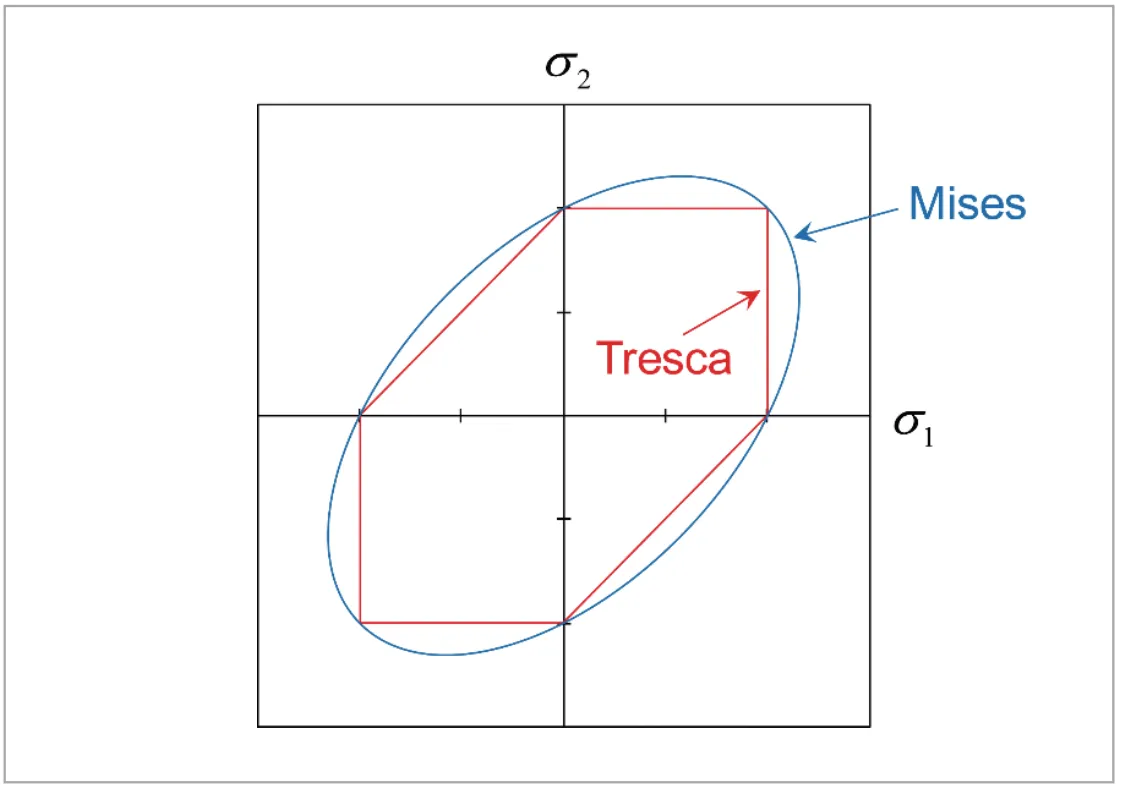
図3 平面応力状態におけるTrescaとMisesの降伏曲面
4.7 TrescaとMisesの降伏関数の比較
図3を見ると、TrescaとMisesの降伏曲面は形状こそ![]() 平面上で正六角形と真円という差異があるものの、本質的には非常によく似た傾向をもつ曲面であることがわかり ます。実際、これらの降伏関数が適用可能な材料の降伏点は、両者の中間に存在することが多いと知られています。ですから、降伏を予測するだけであれば、実はどちらを用いても大きな差はありません。しかしながら、実際にはMisesの降伏関数が用いられることが圧倒的に多数です。 これは、第4 回で取り扱う塑性構成式において、降伏関数の微分が必要となることが大きな理由です。Trescaの降伏関数は、降伏曲面に角があることからわかるように、微分不可能な点が存在します。一方、Misesの降伏曲面は全ての点でなめらかであり、降伏関数が任意の点で微分可能となります。このような数学的な理由(可微分性)から、 Misesの降伏関数は非常に使い勝手がよいのです。
平面上で正六角形と真円という差異があるものの、本質的には非常によく似た傾向をもつ曲面であることがわかり ます。実際、これらの降伏関数が適用可能な材料の降伏点は、両者の中間に存在することが多いと知られています。ですから、降伏を予測するだけであれば、実はどちらを用いても大きな差はありません。しかしながら、実際にはMisesの降伏関数が用いられることが圧倒的に多数です。 これは、第4 回で取り扱う塑性構成式において、降伏関数の微分が必要となることが大きな理由です。Trescaの降伏関数は、降伏曲面に角があることからわかるように、微分不可能な点が存在します。一方、Misesの降伏曲面は全ての点でなめらかであり、降伏関数が任意の点で微分可能となります。このような数学的な理由(可微分性)から、 Misesの降伏関数は非常に使い勝手がよいのです。
第2回は、降伏関数の考え方とTresca、Misesの降伏関数の具体形を解説しました。特にMisesの降伏関数は、今日でも最も重要な降伏関数の1 つです。また、これと密接な関係があるMises応力も非常に便利な量であり、CAEの実用現場において正しく理解して使いこなすことが重要です。次回は、初期降伏以降の応力の変化を表すひずみ硬化則について解説します。ひずみ硬化則の理解にあたっては、今回の降伏関数についての知識も重要となりますので、その基礎をしっかりマスターして頂ければ幸いです。