資料ダウンロード
破壊力学について(4)
破壊力学解析事例(応力拡大係数やJ積分計算、き裂進展解析事例の紹介)

CAEのあるものづくり Vol.27|公開日:2017年12月
目次
- はじめに(破壊力学解析事例)
- VCCM(仮想き裂閉口積分法; Virtual Crack Closure-Integral Method)や相互積分法による 応力拡大係数の計算精度について
- 表面き裂問題で現れる特徴的な応力拡大係数の分布
- 様々なき裂進展解析例(表面き裂、超大規模解析、キンクしながらの進展、複数き裂の成長・合体)
- 非線形破壊力学問題
- 結び
1. はじめに(破壊力学解析事例)
前回まではかなり理論的な話題を提供してきましたが、最終回となる今回は応用や破壊力学解析事例について紹介することにします。前回までに有限要素法解析を用いた応力拡大係数やJ積分といった破壊力学パラメータ解析手法の基礎、さらに二次元から三次元問題への拡張について述べてきました。今回は、それらを用いたき裂問題やき裂進展解析について最近の筆者の解析事例を中心に紹介していきます。はじめに、応力拡大係数の解析精度について計算例とともに紹介します。次に、表面き裂問題で現れる特徴的な応力拡大係数の分布について議論を行い、き裂進展解析でき裂形状がどのように変わっていくかについて一般的な知見を述べます。その中で荷重軸に対して傾いたき裂や複数のき裂が進展の結果どのような形状になるか、等について議論をしていきます。特に結論はありませんが、最後に結びを述べて第一回から四回目となる今回までの締めくくりとさせていただきます。
2. VCCM(仮想き裂閉口積分法; Virtual Crack Closure-Integral Method)や相互積分法による 応力拡大係数の計算精度について
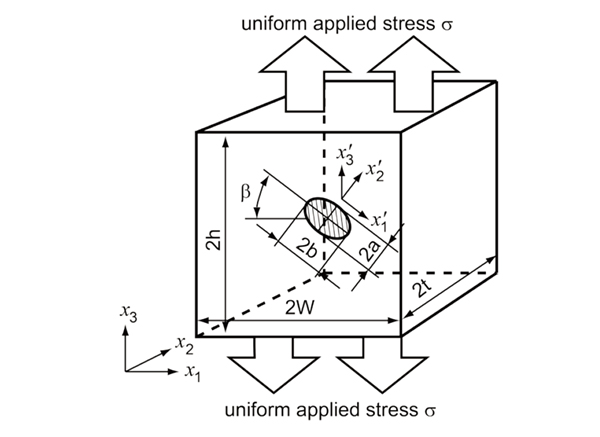
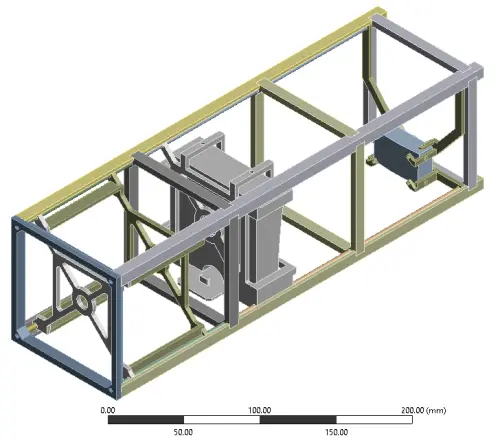
図1遠方で一様引張荷重を受ける、傾いた埋め込みき裂を有する弾性ブロックの問題
はじめに、第三回目まででご紹介した破壊力学パラメータ解析手法でどの程度の精度で解析ができるのか、について紹介します。結論から述べますと、き裂前縁の応力拡大係数の分布をグラフにすると厳密解との違いがわからないくらいの精度で解析が可能です。図1に一様分布荷重を受ける、傾いた埋め込みき裂を有する弾性体ブロック問題の概要を示します。このような問題の解析結果は遠方で一様応力を受ける無限弾性体中の埋め込みき裂の解との比較でそれら数値解析結果の精度を評価することが可能です。
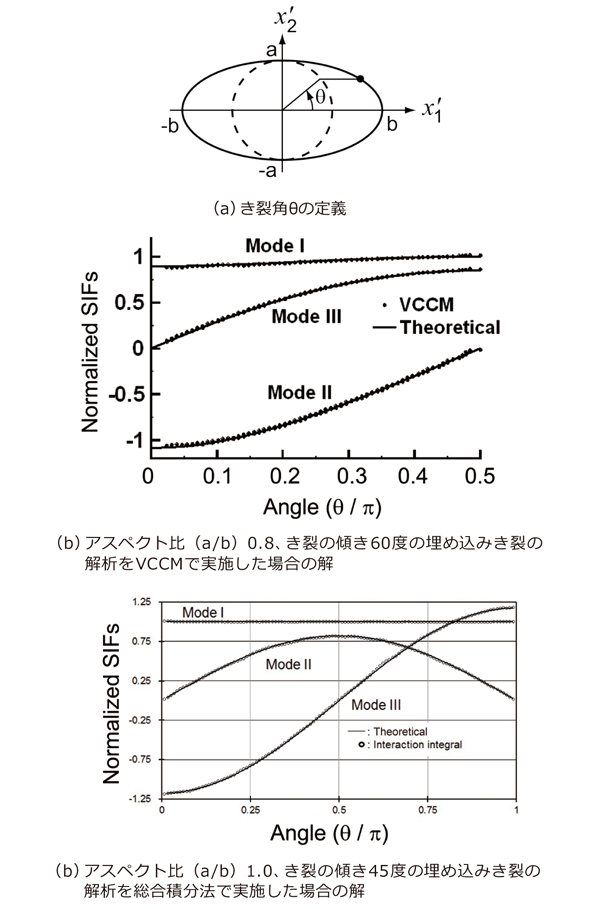
図2 混合モード下のだ円形埋込き裂に対する応力拡大係数計算結果
図2にVCCMと相互積分法で混合モード応力拡大係数の計算を行った結果をそれぞれ示します。解析の詳細については割愛しますが、どちらとも無限弾性体中の埋め込みき裂の解(厳密解)と良く一致しています。グラフにすると、厳密解を表す曲線の上に数値解析で求めたものがほぼ完全に重なってしまっています。これらから、有限要素法を用いた破壊力学パラメータ計算の精度は大変良好であることがわかります。稀に、応力拡大係数の計算結果が±2~3%の誤差を有しても良好な解析結果であるような議論を見かけることがありますが、筆者は少なくとも1%以内の計算精度が得られると考えています。
有限要素法解析の精度解析条件や有限要素法解析モデルに関する詳細についてはOkadaら[1]やDaimonら[2]を参照して下さい。
3. 表面き裂問題で現れる特徴的な応力拡大係数の分布
表面き裂問題の解というと、 有名なRaju-Newmanの解 [3]があります。 例えば、 MurakamiらのStress Intensity Factor HandBook[4]に纏められている表のデータからき裂前縁の応力拡大係数の分布を描くと図 3 中央のようになります…