資料ダウンロード
Ansysにおける1Dモデル化(モデルリダクション)技術

CAEのあるものづくり Vol.24|公開日:2016年5月
目次
- はじめに
- 状態空間実現マトリクス出力機能(SPMWRITE)
- 非線形振動問題
- 非定常熱伝導問題
はじめに
昨今は有限要素法を中心とした数値計算技術と計算機性能の向上を背景に、自動車や電子機器など工業製品の設計開発を中心にCAEが積極的に活用されています。近年では最適化や制御など、従来有限要素法のモデルを使用するには計算時間がかかりすぎて、その適用が躊躇されていた分野にも徐々に適用がみられつつあります。しかし有限要素法のモデルをそのまま適用すると、計算時間が現実の設計期間に収まらないため、使用を断念せざるを得ないケースもしばしば起こるようです。そこで、シミュレーション時間を短縮する方法の1つとして、Ansys ® のモデルリダクション技術について、いくつか事例を交えて紹介します。
状態空間実現マトリクス出力機能(SPMWRITE)
構造解析におけるモード解析の結果から、現代制御理論の状態空間実現マトリクスを出力する機能です。Ansysのモード解析終了後に、出力点(節点とその方向)の指定をすることで、モード解析の固有値と固有ベクトル情報から状態空間実現マトリクスを作成することができます。これらの情報から(所謂1D系のシミュレーションツールを使用して)、現代制御に基づく制御系を構成した制御シミュレーションやPID制御によるシミュレーションも実施することができます。
この機能は、構造解析のみに対応する機能なため、振動制御のシミュレーションに応用可能な機能です。
非線形振動問題
2で紹介した状態空間実現マトリクス機能を応用した例を紹介します。
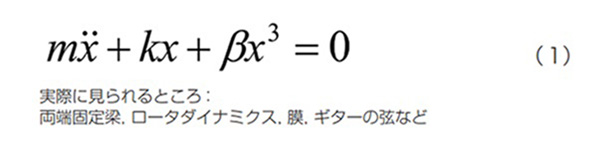
一般に式(1)に示されるような運動方程式はダフィング方程式と呼ばれます。実際の物理現象としては、ロータダイナミクスや膜、ギターの絃などの振動を表現する非線形微分方程式として現れます。特徴は剛性が線形効果のみでなく、非線形効果も併せてもつ方程式です。変形量の三乗に比例した剛性が寄与する方程式となっており、式(1)の方程式は非線形方程式ですが、剛性項が線形項と非線形項に分離できる点に大きな特徴があります。このケースを想定できるAnsysの解析は、材料は線形材料のみを使用し、非線形性は大変形効果のみが適用されるような場合です。材料非線形性や境界非線形(接触)を使用すると、一般に剛性項の分離ができなくなります。このような縮退方法は、駆動する周波数が決まっているような振動問題に特に効果的です。
図1 に示すような圧電式駆動ミラーデバイスを例に解析方法を紹介します。まず、このモデルにおけるモード解析を...