CAEを学ぶ
疲労解析の重要性〜解析に必要な材料データと設定手順〜
本記事では、疲労評価の重要性を認識しながらも、疲労評価(疲労解析)を実施されたことがない方に対し、「事前準備として必要なデータは何か」から「疲労ツールではどのようなことまで評価できるのか」までをAnsysの疲労解析ツールの機能を交えてご紹介いたします。
1.はじめに
疲労破壊とは、『繰り返し荷重が作用することにより、徐々にき裂が進行し破壊に至る現象』ですが、図1にあるデータによると部品破損の80%以上が疲労破壊に起因していることになります。疲労破壊を引き起こさないためにも、各部品に対する疲労寿命の発生予測を行うことは部品設計を行う上で重要であると言えます。
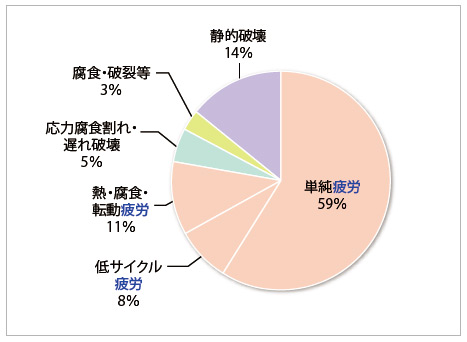
図1 破損の原因別分類
疲労破壊の特徴は、繰り返し荷重により静的な破壊強度や降伏応力以下の荷重負荷においても発生することです。静的な応力評価(静的構造解析)では疲労破壊を予測しきれないため、疲労解析が用いられます。本稿では、疲労解析を実施されたことがない方向けに、解析を実施するために必要なデータの説明とAnsysを用いた疲労解析をご紹介いたします。
2.手計算による疲労評価の限界
疲労評価に必要な事前情報は以下の2点です。
- 構造評価で得られる各部の応力・ひずみ値
応力・ひずみ値は構造解析で得られます。
- S-NまたはE-N疲労線図(図2)
疲労線図は縦軸に応力・ひずみの振幅、横軸にその負荷振幅を繰り返した際の破壊に至るサイクルをまとめた材料物性値です。縦軸が応力のものをS-N線図、ひずみのものをE-N線図と呼びます。線図使い分けの目安として、S-N(応力-寿命)線図は104回以上の高サイクル疲労に使用され、E-N(ひずみ-寿命)線図は104回以下の低サイクル疲労に使用されます。
疲労線図は疲労試験にて取得しなければなりませんが、材料データベースCYBERNET Total Materiaに搭載されている疲労データをご利用いただく方法もあります。
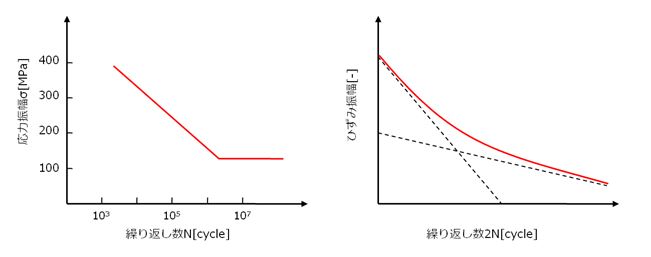
図2. 疲労線図(S-N, E-N)
この疲労線図と構造評価で得られた応力・ひずみ値を比較することで疲労破壊に至るサイクル数、つまり寿命を算出します。図3のように繰り返し荷重が単純な一定振幅の場合、応力値と疲労線図から手計算で疲労寿命を算出可能です。
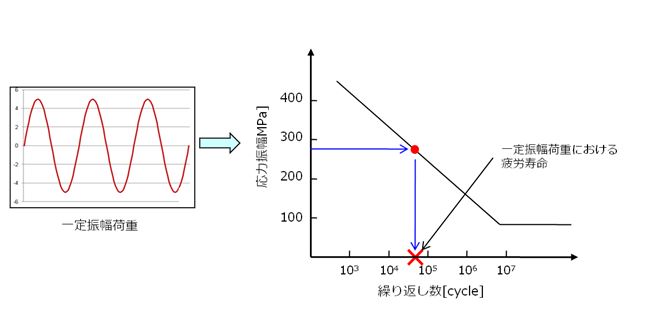
図3. 一定振幅荷重の寿命算出
ところが、図4のように繰り返し荷重が非一定振幅の場合、手計算による寿命算出は容易ではありません。変動する振幅荷重を各々の振幅毎に分解し、それぞれの振幅荷重による損傷度を累積した上で寿命を算出する必要があります。通常は複数個所に対し疲労寿命を算出する必要があり、より手計算での評価が困難であることが予想されます。
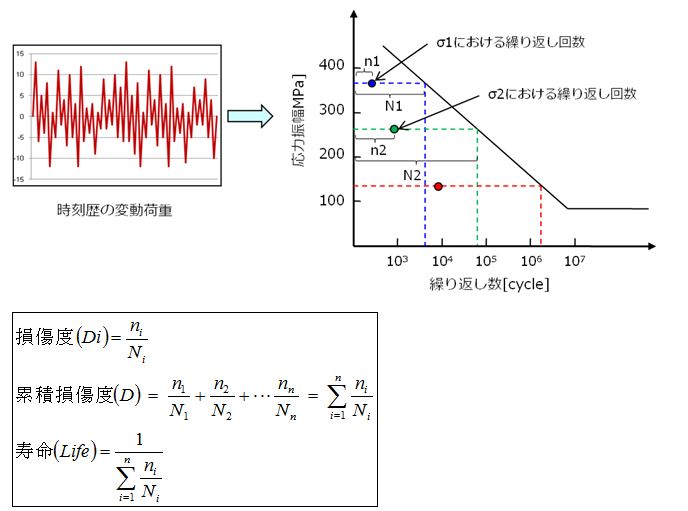
図4. 時刻暦の振動荷重の寿命算出
このような問題に対し、Ansys Fatigue Moduleによる疲労解析を用いれば寿命算出を自動で行えます。
3.Ansys Fatigue Moduleによる疲労解析
Ansys Fatigue ModuleはAnsys Workbench Mechanicalの環境で動作し、非常に簡単に疲労解析を実施することが可能です。Ansys Fatigue Moduleによる一連の疲労解析の手順を説明します。
手順1:材料設定(疲労線図の追加)
構造解析用の材料物性の設定と同様に、疲労解析用の物性値を設定します。手動定義および事前定義した材料データベースからの読み込みのどちらでも設定が可能です。
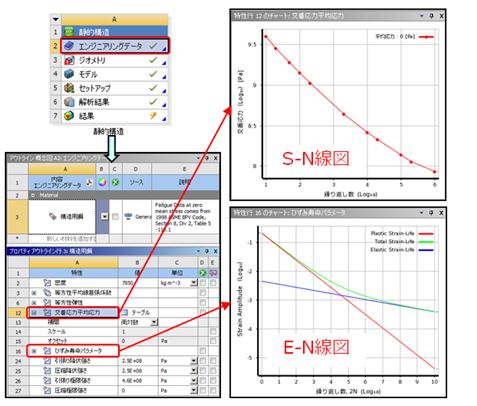
図5. 疲労線図の設定
手順2:構造解析
疲労寿命算出に必要となる応力・ひずみ結果を構造解析により算出します。通常の静的構造解析と同様です。
手順3:疲労解析設定
事前に設定した疲労線図および、構造解析により得られた応力・ひずみを元に疲労解析の設定を行います。設定項目は疲労寿命の影響因子である平均応力補正理論の指定と、荷重の繰り返し条件の指定の2つです。
・平均応力補正理論
一般的に、疲労寿命は同じ応力振幅の場合でも引張りの平均応力が作用すると低下し、圧縮の平均応力が作用すると同じか増加します。つまり、平均応力が発生している場合にはそれを考慮しなければ正しい疲労寿命を得られません。この補正に使用されるのが平均応力補正理論であり、図6のようにS-N線図、E-N線図それぞれに対応したものがあります。Ansys Fatigue Moduleでは事前定義されたこれらの平均応力補正理論を指定するだけで、補正効果を考慮した寿命を算出することが可能です。
−S-N線図の平均応力補正理論:Goodman 、Soderberg 、Gerber
−E-N線図の平均応力補正理論:Morrow 、SWT(Smith Watson Topper)
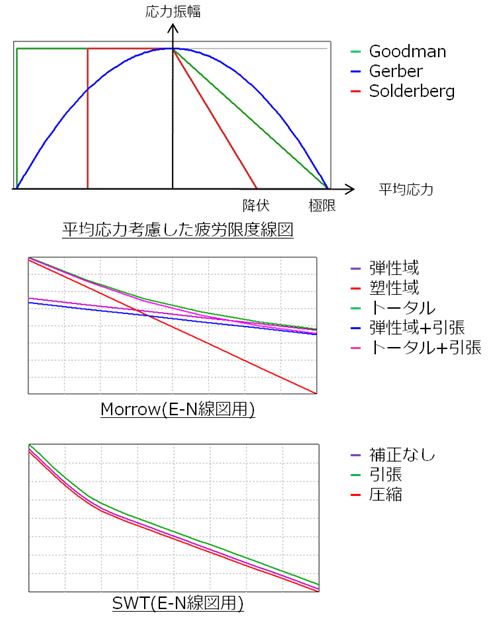
図6. 平均応力補正理論
・荷重の繰り返し条件
構造解析で得られた応力・ひずみ結果を元にした繰り返し条件を設定します。
一定振幅荷重
構造解析の応力値に対し、正負のスケールファクターを掛けることで平均応力値や応力振幅を考慮した一定振幅の繰り返し荷重を与えます。入力形態としては利用頻度の高い[両振り]、[片振り]、およびユーザー側で正負の比率を制御可能な[比率]があります。
荷重履歴データによる非一定振幅荷重
構造解析の応力値に対し、時刻暦で変化するスケールファクターを掛けることで非一定振幅荷重を与えます。
設定は時刻暦で変化するスケールファクターを記述したテキストデータの読み込みにより簡単に行えます。前述のように手計算による評価が困難であるため、疲労解析の効果がもっとも出やすい条件です。
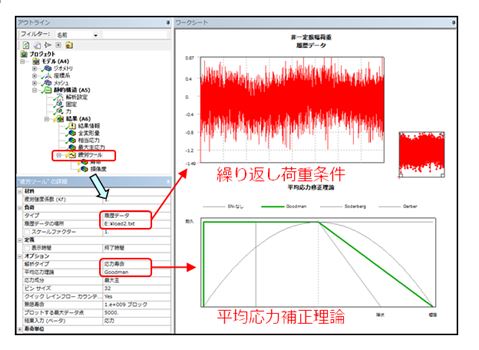
図7. 疲労条件の設定
手順4:結果処理
得られる疲労結果としては使用頻度の高いものに寿命、損傷度、レインフローマトリクスが挙げられます。
・寿命
負荷された繰り返し荷重下での破壊に至るまでのサイクル数をモデル上にコンター表示します。
・損傷度
1サイクルにおける損傷度合いをコンター表示します。寿命の逆数であり、損傷度1で疲労破壊したと見なします。
・レインフローマトリクス、損傷度マトリクス
非一定振幅の荷重が負荷された際に利用する機能です。非一定振幅荷重をレインフロー法によりサイクルに分解し、各平均応力・応力振幅とその発生サイクル数もしくは損傷度で表したものです。寿命強度に影響の大きい負荷条件を検出し、疲労寿命の分析や対策に利用できます。
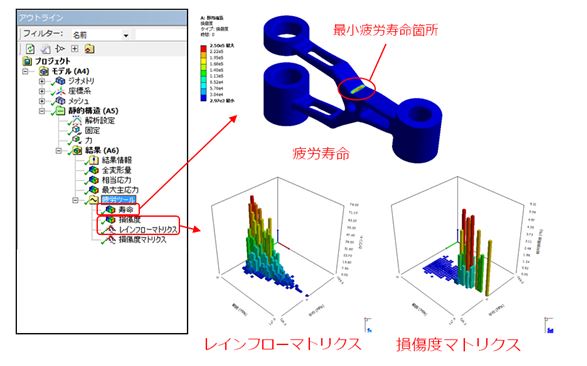
図8. 疲労解析結果
このようにAnsys Fatigue ModuleによりAnsys Workbench Mechanicalの環境下で簡単に疲労解析を実施できます。
4.Ansys Fatigue Moduleによる振動疲労解析
Ansys Fatigue Moduleは、振動解析結果を元にした動的な挙動を考慮した振動疲労解析にも対応しています。
輸送時や使用時に製品が受ける荷重は周期性がなく、様々な周波数成分を含んだランダムな振動が原因となって疲労破壊が生じます。このような荷重における疲労を評価する場合、時刻歴の負荷荷重に対する応答をそのまま解く時刻歴解析を行って疲労評価する方法が考えられますが、計算コストが高くなってしまいます。そこで、統計的な手法により入力PSD(パワースペクトル密度)を使った計算手法であるランダム振動解析がよく利用されます。
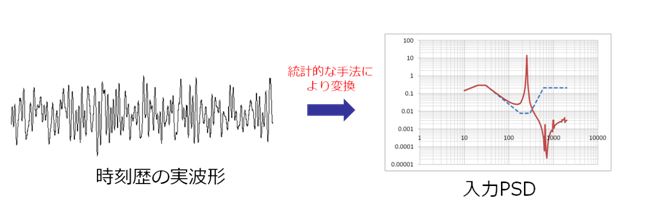
図9. 入力PSDの例
ランダム振動疲労解析のフロー
ランダム振動疲労解析のフローは図10のようになります。ランダム振動疲労解析では、元となる構造解析はランダム振動解析になります。(ランダム振動解析の前提としてモーダル解析が必要)
ランダム振動解析により得られた「応答PSD」と疲労物性値である「SN線図」を入力とし、「疲労ツール」によりランダム振動における疲労寿命を算出します。
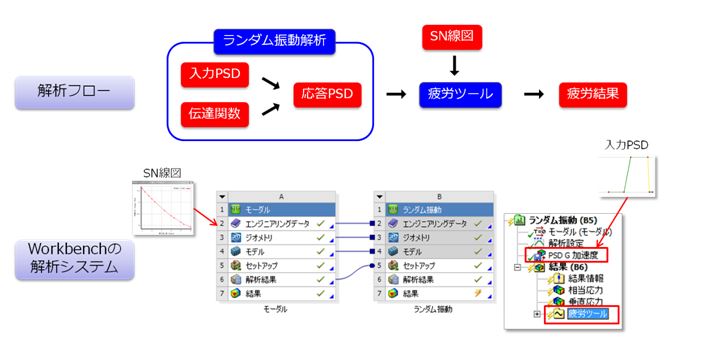
図10. ランダム振動解析のフロー
・疲労結果評価手法
疲労結果を評価する手法としてSteinberg、Narrow-Band、Wirschingが利用できます。よく利用される手法であるSteinbergは、時刻歴履歴における応力範囲がガウス分布に従うという仮定で発生頻度を推定します。各応力範囲の発生頻度とSN線図の関係、そして別途設定する被荷重期間からマイナー則による寿命を算出します。
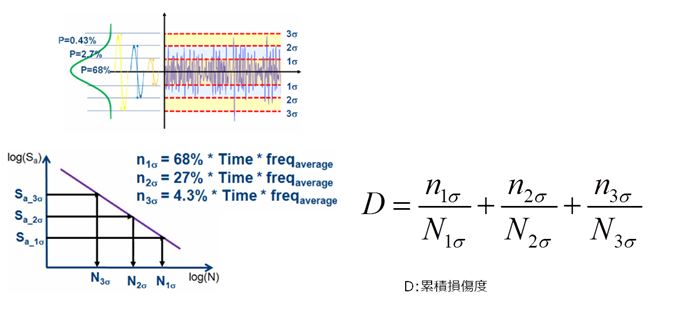
図11. Steinbergによる疲労評価
ランダム振動疲労解析の結果
ランダム振動解析で得られる結果は、寿命および損傷度です。
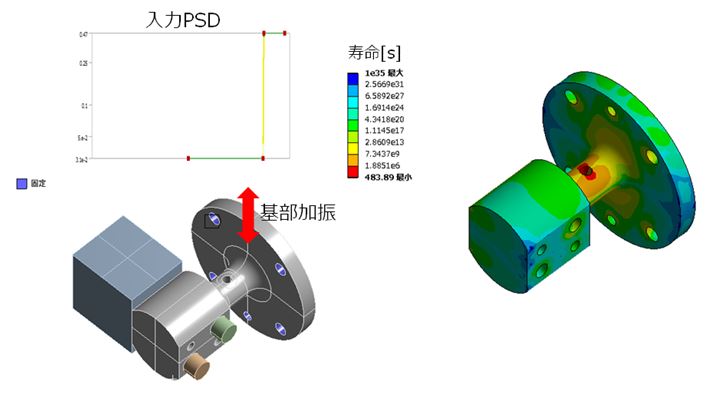
図12. ランダム振動解析例
5.おわりに
本稿では疲労評価の必要性およびAnsys上で利用可能な疲労解析ツールであるAnsys Fatigue Moduleの有用性について説明しました。疲労評価でお困りのお客様にとってお役にたてれば幸いです。
参考文献
1) 日本機械学会、技術資料:機械・構造物の破損事例と解析技術、日本機械学会 (1984).)
過去のセミナー講演資料(ご請求)
Ansys Convergence (Japan Ansys Conference)
製品開発における疲労強度評価セミナー
〜疲労強度評価の理論から、実験事例、解析手法まで〜



