粘弾性モデルの基礎(前編/後編) 完全保存版 PDF を無料公開中
粘弾性モデルの基礎(前編/後編) 完全保存版 PDF サンプル
これさえ読めば粘弾性モデルの基礎がわかる
全2回のシリーズとなっております「粘弾性モデルの基礎」について、前編/後編を1冊でお読みいただける完全保存版 PDF を公開いたしました。どなたでも簡単なフォーム入力のみでダウンロードいただけますので、是非この機会にご利用ください。
【ページ数】13 ページ
【ファイル形式】 PDF
【著者】佐賀大学 大学院工学系研究科 機械システム工学専攻
只野 裕一 様
|
【目次】
1. はじめに
2. 線形粘弾性モデルの構成要素
3. 線形粘弾性モデルの定式化
3.1 Maxwellモデル
3.2 Voigtモデル
4. MaxwellモデルとVoigtモデルの材料応答
4.1 Maxwellモデルの材料応答
4.2 Voigtモデルの材料応答
|
5. 時間変化する入力を 与えたときの材料応答
5.1 Maxwellモデルの材料応答
5.2 Voigtモデルの材料応答
6. 線形粘弾性モデルの一般化
6.1 一般化Maxwellモデル
6.2 一般化Voigtモデル
6.3 一般化Maxwellモデルと一般化Voigtモデルの材料応答
7. 線形粘弾z性モデルの 3次元モデルへの
7.1 Maxwellモデルの3次元モデルへの拡張
7.2 Voigtモデルの3次元モデルへの拡張
8. おわりに
|
時間変化する入力を与えたときの材料応答
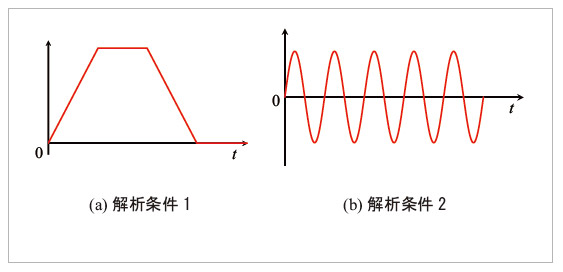
前編では、MaxwellモデルとVoigtモデルに対して、一定応力や一定ひずみという最も単純な入力を与えた場合の応答について考えました。粘弾性モデルは時間依存変形を表現するモデルですので、時間とともに変化する入力を与え、もう少し一般的な条件に対する材料応答を見てみましょう。ここでは、図9に示す2つの解析条件を考えます。
(a)の解析条件1では、ある時刻から線形的に入力が増加したのち一定値でしばらく停止します。その後入力が0になるまで直線的に減少し、0で一定時間保持する、という条件です。(b)の解析条件2は正弦波による周期的な入力となっており、振動に相当する条件です。これらの解析条件を、Maxwellモデルではひずみの入力として、Voigtモデルでは応力の入力として与えます。以降の各解析では、弾性体に対する応答もあわせて黒い実線で図中に示します。弾性体は入力に対して瞬時に応答するため、入力と出力の形は必ず相似となります。
5.1 Maxwellモデルの材料応答
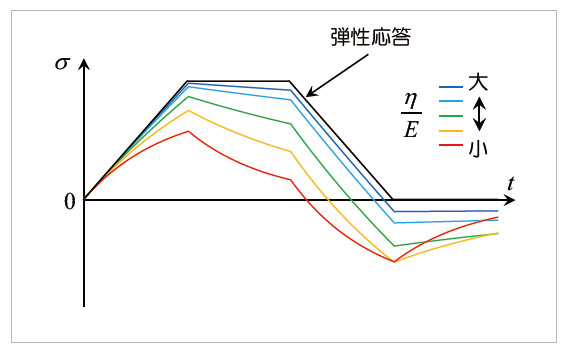
図10 Maxwellモデルによる応力応答(解析条件1)
まず、Maxwellモデルに解析条件1をひずみ入力として与えた場合の応力応答を図10に示します。黒い実線の弾性応答は、入力と相似な形状となることがわかります。これに対してMaxwellモデルの結果を見てみると、はじめの立ち上がりが弾性応答と比較して遅れており、また直線的でもないことがわかります。これは、ひずみ入力の上昇にともなって応力が増加する一方で、応力緩和も生じるためです。つぎの一定ひずみで保持する過程では徐々に応力が低下していますが、これも応力緩和によるものです。結果として、このひずみ一定の過程でも応力応答は一定とはなりません。ひずみが減少する過程でも、上昇時と同様に応力緩和が生じるため直線的な減少とはならず、さらに入力は常に正の値にもかかわらず、応力応答が負になる場合があります。最後のひずみを0で保持する過程では、応力緩和によって応力が0へと漸近していきます。いずれの過程においても、η/Eが小さくなるほど弾性応答との差異は大きくなります。
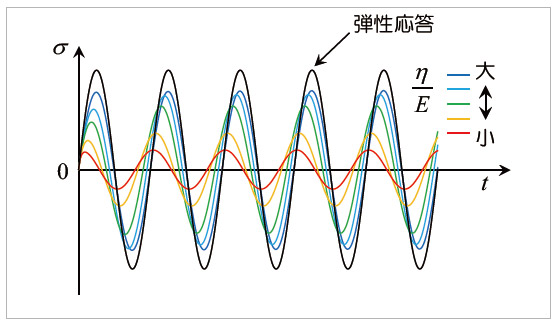
図11 Maxwellモデルによる応力応答(解析条件2)
つぎに、Maxwellモデルに解析条件2をひずみ入力として与えてみましょう。このときの応力応答が図11です。解析条件1と同様に、η/Eが小さくなるほど弾性応答との差異が大きくなります。もう少し具体的には、η/Eが小さくなると応力の振幅が小さくなり、さらに位相も入力とずれていくことがわかります。このように、周期的な入力に対して出力の位相がずれることは、粘弾性の特徴的な挙動の一つです。ここで示した2つの結果において、いずれの場合もη/Eが小さくなるほど弾性応答との差異が大きく現れました。η/Eは前編の4.1節で示した緩和時間に相当する量となっており、緩和時間が大きいほど弾性応答に近づくことに対応しています。すなわち粘性係数が相対的に大きいほど、材料応答は弾性に近づきます。
5.2 Voigtモデルの材料応答
続いて、Voigtモデルに解析条件1を応力の入力として与えた場合を考えます。図12はこの時のひずみ応答です。はじめの立ち上がりが弾性応答と比較して遅れ、直線的な応答にならないことはMawellモデルと同様ですが、ある程度時間が経過すると弾性応答と同じひずみが生じる点が、Maxwellモデルとは異なります(Maxwellモデルは応力緩和が生じるため、時間の経過と共に弾性応答から離れていきます)。つぎの応力一定の過程でも、ひずみが弾性応答に達していればその後のひずみも一定となり、ひずみの減少は生じません。これらの傾向は、応力を減少させる過程や0で保持する過程でも同様です。すなわち、Voigtモデルに応力の入力を与える場合、十分に時間が経過すると弾性応答が生じますが、粘性の影響によって入力に追従するのに時間を要することがわかります。またMaxwellモデルとは逆に、η/Eが大きくなるほど弾性応答との差異は大きくなります。つぎに、Voigtモデルに解析条件2を応力入力として与えた際のひずみ応答を図13に示します。解析条件1と同様に、η/Eが大きくなるほど弾性応答との差異が大きくなります。また、η/Eが大きくなるほど応力の振幅が小さく、さらに位相も入力とずれていくこともわかります。すなわち、周期的な入力に対して出力の位相がずれるという挙動は、Maxwellモデルと同様です。ここで示した2つの結果において、いずれの場合もη/Eが大きくなるほど、弾性応答との差異が大きく現れました。η/Eは前編の4.2節で示した遅延時間に相当する量であり、遅延時間が小さい、すなわち粘性係数が相対的に小さいほど、材料応答は弾性応答に近づきます。
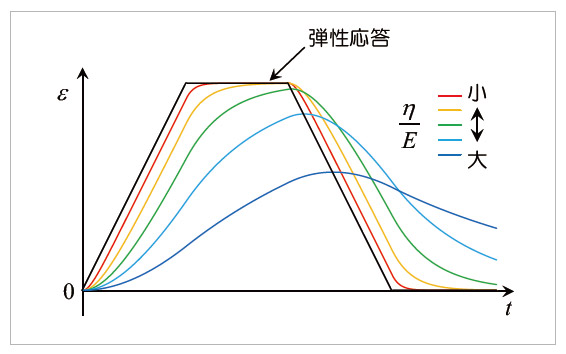
図12 Voigtモデルによるひずみ応答(解析条件1)
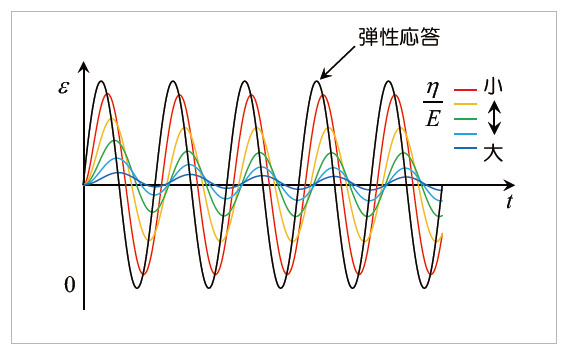
図13 Voigtモデルによるひずみ応答(解析条件2)
線形粘弾性モデルの一般化
以上で示したMaxwellモデルとVoigtモデルは、それぞれ粘弾性モデルの基本的な構成要素であるばねとダッシュポットを1つずつ直列、もしくは並列に結合したモデルでした。非常にシンプルなモデルであり、応力緩和や遅延弾性など粘弾性の基本的な性質を定性的に表現できるものの、現実の粘弾性材料の挙動を定量的に評価するには、残念ながら多くの場合不十分です。そこで、より現実的な材料応答を表現するために、一般化Maxwellモデルや一般化Voigtモデルがしばしば利用されます。これらのモデルは、複数のMaxwellモデルやVoigtモデルを結合する(結果として複数のばねとダッシュポットが結合する)というのが基本的なアイデアとなります。
6.1 一般化Maxwellモデル
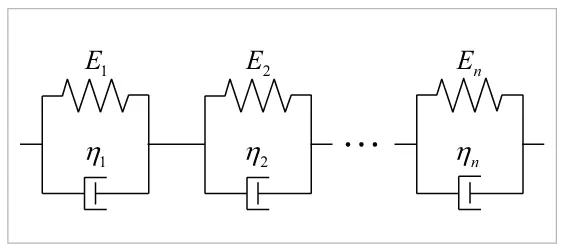
一般化Maxwellモデルは、図14に示すように複数のMaxwellモデル(以降、それぞれのMaxwellモデルのことをMaxwell要素と呼びます)を並列に結合したモデルです。各Maxwell要素のばね定数と粘性係数は一般に異なります。ばねだけの要素とダッシュポットだけの要素をそれぞれ1つずつ含むようモデル化する場合もありますが、Maxwellモデルにおいて粘性係数を十分に大きくすると線形弾性モデルに、弾性係数を十分に大きくすると線形粘性モデルにそれぞれ帰着することから、ばねだけやダッシュポットだけの要素もMaxwell要素の特別な場合と考えることができます。また結合する要素の数は任意であり、理論上はその数はいくつでも構いません。
各Maxwell要素が並列に結合されているため、各要素に生じるひずみはモデル全体のひずみεと等しくなります。すなわち、要素数がn個の一般化Maxwellモデルに対して
となります。応力やひずみの右下添え字は、各要素の番号を表しています。一方、モデル全体に生じる応力は各Maxwell要素に生じる応力の和となります。
このようなモデルを考えると、モデル全体の弾性係数は各Maxwell要素の弾性係数の和となります。
このことから、各Maxwell要素の弾性係数は異なって構いませんが、その総和は実際の材料の弾性係数と一致するように決定することになります。
6.2 一般化Voigtモデル
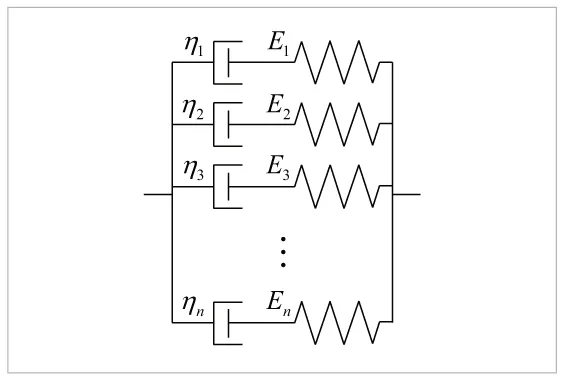
一般化Voigtモデルは、図15に示すように複数のVoigtモデルを直列に結合したモデルです。各Voigt要素のばね定数と粘性係数は、それぞれ異なって構いません。また一般化Maxwellモデルと同じように、ばねだけの要素とダッシュポットだけの要素をそれぞれ1つずつ含むようモデル化する場合もあります。Voigtモデルにおいては、粘性係数を0にすると線形弾性モデルに、弾性係数を0とすれば線形粘性モデルにそれぞれ帰着することから、ばねだけやダッシュポットだけの要素もVoigt要素の特別な場合と考えることができます(Maxwellモデルとは傾向が逆なので注意してください)。一般化Maxwellモデルと同様に、結合する要素の数はいくつでも構いません。
各Voigt要素が直列に結合されていることから、各要素に生じる応力がモデル全体の応力σと等しくなります。すなわち、要素数がn個の一般化Voigtモデルに対して
となります。一方、モデル全体に生じるひずみは各Voigt要素に生じるひずみとなるので、
で与えられます。一般化Voigtモデルでは、モデル全体の弾性コンプライアンス(弾性係数の逆数)が各Voigt要素の弾性コンプライアンスの和となります。
すなわち、各Voigt要素の弾性コンプラインスの総和が、実際の材料の弾性コンプライアンスと一致するよう弾性係数を決定することになります。
6.3 一般化Maxwellモデルと一般化Voigtモデルの材料応答
一般化Maxwellモデルと一般化Voigtモデルの材料応答について、簡単な例題で見てみましょう。前節の図9(a)で示される入力を考え、一般化Maxwellモデルにはひずみ入力を、一般化Voigtモデルには応力入力を与えてみます。前述の通り一般化Maxwellモデルや一般化Voigtモデルにおいて結合する要素の数は任意ですが、ここでは簡単のためにそれぞれ要素数は2とします。
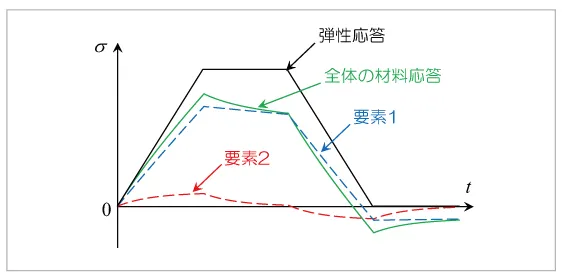
2要素で構成される一般化Maxwellモデルにひずみ入力を与えた際の、応力応答を図16に示します。要素1は弾性係数、粘性係数がともに要素2よりも大きい要素としています。2つのMaxwell要素がそれぞれ単体で存在するときの材料応答がそれぞれ青と赤の破線であり、全体の材料応答(緑の実線)はその和となっています。要素1の応力が全体的に要素2よりも高くなっていますが、これは要素1の弾性係数が要素2の弾性係数より大きいためです。すなわち、モデル全体の材料応答に各要素がどの程度寄与するかは、各要素の弾性係数の大きさによって決まることになります。要素数を増やした場合にも、全体の材料応答は常に各要素の応答の総和として与えられます。これにより、単体のMaxwellモデルでは表現できなかった複雑な材料応答を表現することが可能となります。
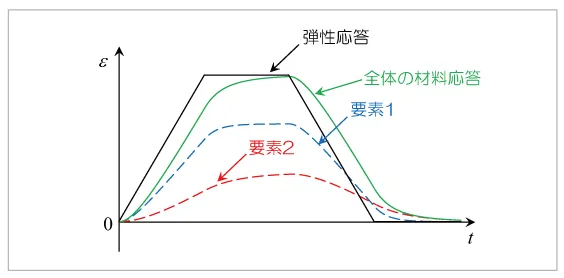
図17は、2要素で構成される一般化Voigtモデルに応力入力を与えた際のひずみ応答です。ここでは、要素1は弾性係数、粘性係数がともに要素2よりも小さい要素としています。一般化Maxwellモデルと同様、全体の材料応答は要素1と要素2の応答の和となっていることがわかります。また、各要素が全体の材料応答にどの程度寄与するかは、各要素の弾性コンプライアンスの大きさで決まります。要素数が増加した場合でも、各要素の材料応答の総和が全体の応答として得られ、これにより単体のVoigtモデルでは表現できない複雑な応答を表すことができます。
一般化Maxwellモデルや一般化Voigtモデルは、要素の数が増えるほど材料定数の数も増加するため、より複雑な材料挙動を表現しようとすると材料定数の同定が難しくなる傾向があります。手作業での材料定数同定には限界があるため、最適化手法を導入し、いくつかの材料試験の結果から数値的にパラメータを決定することがしばしば行われます。また最近の汎用CAEソフトウェアでは、最適化手法による材料定数の自動同定を標準機能として備えている場合もありますので、そのような機能を利用することで効率的な材料定数の決定を行うことができます。
線形粘弾性モデルの3次元モデルへの拡張
ここまでに示した線形粘弾性モデルは、いずれも1次元的な応力・ひずみ応答に限定して解説してきました。モデルの性質を理解する上で1次元モデルは非常に有効ですが、現実的な変形解析のほとんどは2次元もしくは3次元問題となるため、実用的な材料モデルとしては1次元モデルを3次元モデルへと拡張することが必要になります。そこで本節では、線形粘弾性モデルの3次元モデルへの拡張について考えてみましょう。なお本稿では最も簡単な拡張として、等方粘弾性モデルに限って説明します。また、以下ではMaxwellモデルおよびVoigtモデルについて示しますが、一般化Maxwellモデルや一般化Voigtモデルでも考え方は全く同じです。
線形粘弾性モデルを3次元へ拡張する場合、一般に応力とひずみを体積成分と偏差成分に分離し、それぞれに対して1次元の場合と同様のモデルを仮定します。これは、弾塑性モデルを1次元から3次元へと拡張するときと同じ考え方です。応力の体積成分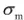 と偏差成分
と偏差成分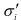 は、それぞれ次式で定義されます。
は、それぞれ次式で定義されます。
ひずみの体積成分は平均ひずみであり、体積ひずみの1/3となります。また応力と同様に、偏差ひずみのせん断成分はもとのひずみのせん断成分と等しくなります(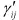 =
=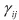 ( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。
( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。
7.1 Maxwellモデルの3次元モデルへの拡張
1 次元のMaxwellモデルの構成方程式はつぎで与えられました。
3次元モデルでは、平均応力と平均ひずみ、偏差応力の各成分と偏差ひずみの各成分について、それぞれ式(27)が成り立つと考えます。すなわち、つぎの構成方程式を与えます。
7.2 Voigtモデルの3次元モデルへの拡張
1次元のVoigtモデルの構成方程式は次式で与えられます。
Maxwellモデルと同様に、3次元モデルでは、平均応力と平均ひずみ、偏差応力の各成分と偏差ひずみの各成分について、それぞれ式(31)が成り立つと考えます。
ここでも材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。また、体積変形には粘性の効果が無視できると考える場合には、式(34)の右辺括弧内の第2項を無視します(体積粘性係数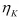 を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。
を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。
おわりに
本稿では、高分子材料などの解析で非常に重要な材料モデルの1 つである線形粘弾性モデルについて理解して頂くことを目的に、その理論の概要といくつかの数値解析例を示しました。一般化Maxwellモデルや一般化Voigtモデルを用いることで、ひずみ速度依存性をもつ現実の材料の複雑な挙動を表現することが可能となりますが、扱う材料や現象によっては、これらのモデルでもまだ精度が十分ではないこともあります。このため、より高精度な材料モデルを構築する研究が今日でも精力的に続けられています。しかし、粘弾性モデルの基礎となるのは線形粘弾性モデルですので、高分子材料などをCAEで扱うのであれば、まずは線形粘弾性モデルの性質をきちんと理解することが重要となります。本稿が、線形粘弾性モデルを理解する助けに少しでもなるのであれば幸いです。
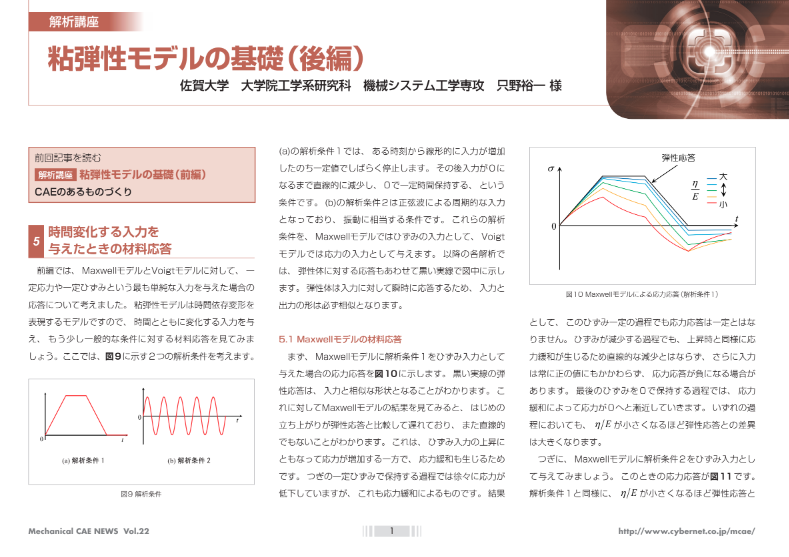





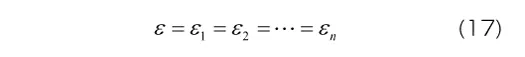
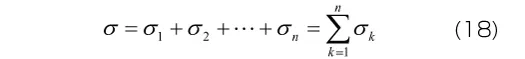
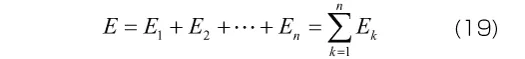
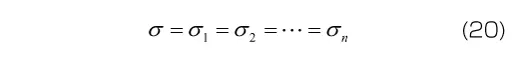
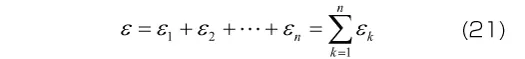
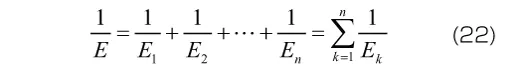
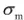 と偏差成分
と偏差成分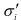 は、それぞれ次式で定義されます。
は、それぞれ次式で定義されます。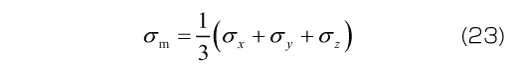
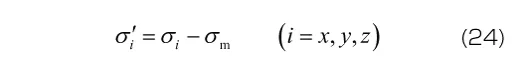
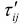 =
=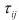 ( i , j = x , y , z ) )。同様にして、ひずみの体積成分
( i , j = x , y , z ) )。同様にして、ひずみの体積成分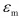 と偏差成分
と偏差成分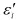 も定義できます。
も定義できます。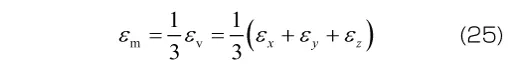
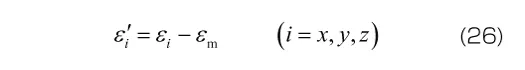
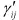 =
=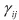 ( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。
( i , j = x , y , z )。以上を用いて、MaxwellモデルとVoigtモデルを3次元モデルに拡張してみましょう。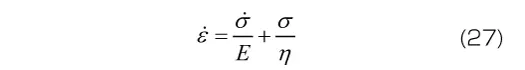

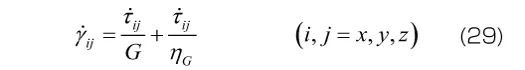
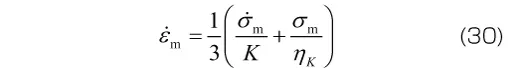
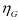 ,
,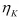 はせん断粘性係数、体積粘性係数と呼ばれます。材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。なお、体積変形には粘性の効果はほとんど現れないと考え、体積変形に対する変形を表す式(30)の右辺括弧内の第2項を無視する(すなわち体積粘性係数
はせん断粘性係数、体積粘性係数と呼ばれます。材料定数が体積変形とせん断変形のそれぞれに必要となるため、材料定数の数は2倍になります。なお、体積変形には粘性の効果はほとんど現れないと考え、体積変形に対する変形を表す式(30)の右辺括弧内の第2項を無視する(すなわち体積粘性係数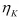 が十分に大きく、弾性応答が得られると考える)こともあります。この場合、材料定数の数は1次元モデルと同じになります。
が十分に大きく、弾性応答が得られると考える)こともあります。この場合、材料定数の数は1次元モデルと同じになります。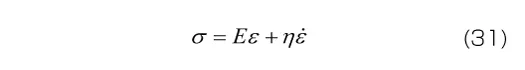
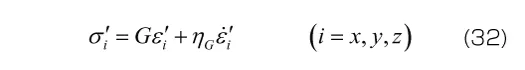
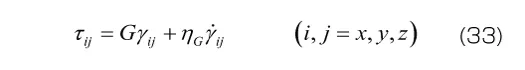
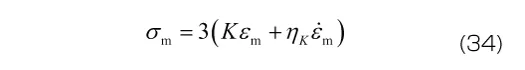
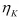 を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。
を0とすることで、弾性応答に帰着させる)。この場合、材料定数の数は1次元モデルと同じになります。