CAEを学ぶ
はじめてみよう!流体解析(実践編)〜誤差との上手なつき合い方(4)モデル化による誤差について〜
はじめに
誤差との上手なつきあい方も第4回です。第2回ではモデル形状の違いによる誤差の中から、特に形状簡略化による誤差、第3回ではメッシュによる誤差の中からレイヤーメッシュの有無による誤差にスポットをあてて解説しました。
今回はモデル化による誤差について考えていきたいと思います。なおここで言うモデル化とは実現象を解析に落とし込むための作業を指す広義のモデル化ではなく、流体解析ツールで解析を行う際の条件設定における乱流モデルや物性値、圧縮性(非圧縮性)、境界条件などの選択を指します。
モデル形状による誤差とは
モデル化による誤差の原因には、例えば以下が挙げられます。
A:乱流モデルの選択による誤差
B:圧縮性(非圧縮性)による誤差
C:ブシネスク近似による誤差
D:境界条件による誤差
E:初期条件による誤差
A:乱流モデルの選択による誤差
実際の流れ場では、大小さまざまな渦がランダムに発生します。この状態を乱流といいます。乱流の渦は時間的にも空間的にも複雑で不規則な動きをします。この乱流を解析する手法として大きく分けて以下の3つがあります。
- 直接数値シミュレーション(Direct Numerical Simulation:DNS)
- 格子平均モデル(Large Eddy Simulation:LES)
- レイノルズ平均モデル(Reynolds-Averaged Navier-Stokes:RANS/Reynolds Stress Model:RSM)
1.のDNSは乱流モデルを使わず、ナビエストークス方程式を直接数値的に解く手法です。メッシュを細かくすれば小さな渦まで表現できますが、解析コストが非常に高く、工業的な利用には向いていません。
そのため現実的な解析コストで、設計で必要とされる流路全体の大まかな流れや熱の伝わりを求めることができるよう、乱流をなんらかの形でモデル化、つまり平均化を行う必要がでてきます。ただし、乱流をモデル化した時点で、どのようなモデルでも誤差を含むことは避けられないことを覚えておきましょう。
乱流のモデル化には大きく分けて、2.の格子平均モデル(LES)と3.のレイノルズ平均モデル(RANS/RSM)の2つがあります。2.のLESは空間的に平均化された方程式を解く手法で、大きな渦は直接計算され、メッシュより小さな渦は乱流モデルで表現します。1.のDNSよりは解析コストが低くなりますが、三次元非定常解析が前提条件となるため、実用的には大規模な解析環境が必要となります。
3.のRANS/RSMはアンサンブル平均された方程式を解く手法で、乱流の影響はすべて乱流モデルで表現します。二次元・定常解析も可能なため、産業分野で一般的に活用されています。
乱流モデルは流れ場に応じて様々なものが提案されていますが、すべての流れ場に適するモデルは未だに開発されておらず、モデル化の手法によって再現できる流れが異なります。
例えばRANSでは空間的・時間的に平均化を行います。計算コストの削減などメリットがありますが、流れの時間的な変化(非定常性)が平均化されてしまうため、非定常解析を行う場合には注意が必要です。流れの非定常性を確認したい場合は、時間的平均化を行わないLESなどを使う必要があります。
剥離流れや旋回流にはLESやRSM(レイノルズ応力モデル。異方性のある流れの解析に適する)、壁面の熱伝達係数を確認したい場合はRNASの中でも低Re k-εが適しています。
このように解析する流れ場に適した乱流モデル(=実際の流れ場の様子を再現できる乱流モデル)を選択することが必要です。
また精度の良い乱流モデルほどメッシュを細かくしたり、非定常計算が必要になったりと解析コストの増加につながります。【再現したい流れ場】をきちんと把握し、【解析コストとのバランス】をみながら乱流モデルを決定することが重要です。
乱流モデルについては以下セミナーで詳しくご紹介しておりますので、こちらもご参考にして下さい。
B:流体の圧縮性(非圧縮性)による誤差
現実の流体は圧力や温度によって流体密度が変化する圧縮性を持っています。しかし流体解析では解析コストを減らすために、流体密度が圧力などによって変化しないとみなせる場合、流体を密度が一定の非圧縮性流体として扱うことが可能です。
流体を液体と気体に分けて圧縮性流体として扱う必要がある場合、ない場合について考えてみましょう。
- 流体が液体の場合
- 流体が気体の場合
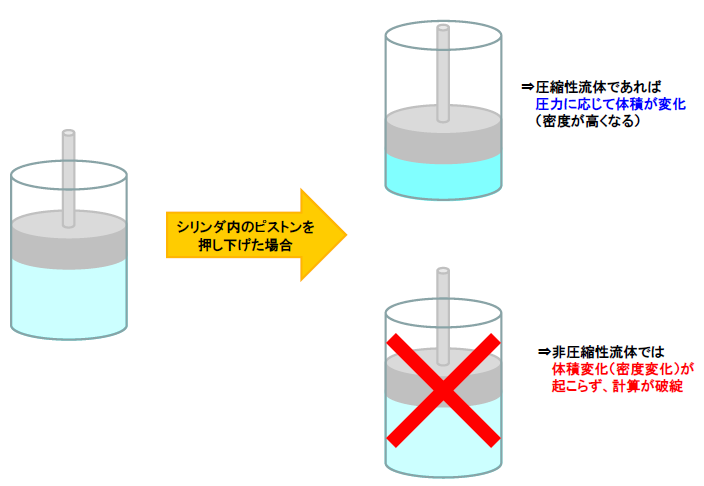
1.流体が液体の場合、圧力や温度による流体密度の変化は無視できると考えられるため、基本的には非圧縮性流体として扱えます。
ただし図1のシリンダー内のピストンを押し下げる解析のように、密閉空間で圧力を加えていくような解析では圧縮性を考える必要があります。この例では、流体を圧縮性流体と考えた場合、流体の体積は圧力によって変化し、流体密度が高くなります。この時、加えた圧力は音速の速さで流体中を伝わります。しかし流体を非圧縮性流体と考えた場合、流体密度は圧力によって変化しないため、解析することができません。
2.流体が気体の場合、流速が遅ければ非圧縮性流体として扱えますが、マッハ数が0.3以上(密度の相対変化が5%以上に相当)になると圧縮性の影響が無視できなくなります。マッハ数は流速を音速で割ったもので、例えば20℃の空気中では音速は約340[m/s]ですので、流速が約100[m/s]以上になるとマッハ数が0.3以上となり、圧縮性の影響が出てくると考えられます。
また圧縮性を考えなければいけない場合として、水撃作用(ウォーターハンマー)や衝撃波、チョーク流れの解析が挙げられます。
これらの現象には流体の圧縮性が大きく関わっているため、圧縮性を考慮した解析が必要となります。
このように解析する流れ場で流体の圧縮性が重要かを検討し、【流れ場が再現できるか】と【解析コストとのバランス】をみながら、圧縮性流体を使用するか非圧縮性流体を使用するかを決定することが重要です。
C:ブシネスク近似による誤差
流体の流れは、駆動方法によって自然対流と強制対流の2つに分けられます。自然対流は流体の密度差によって生じる浮力によって発生する流れで、強制対流はファンやポンプなど外部からの力によって発生する流れです。
自然対流の解析を行う場合、圧縮性流体では温度差による密度変化を考慮するので浮力を厳密に解析することが可能ですが、非圧縮性流体では温度差による密度変化を考慮することができません。そのため非圧縮性流体を用いた自然対流の解析では、浮力を温度差に比例する力で近似する”ブシネスク近似”を用います。
ブシネスク近似では、温度変化によって発生する密度差に比べて圧力変化によって発生する密度差は小さいため無視することができる、また密度差は重力に比例した浮力としてのみ流体の運動に影響を及ぼす、と考えて外力項における浮力を体積膨張率と温度変化で表現します(式1、式2 参照)。
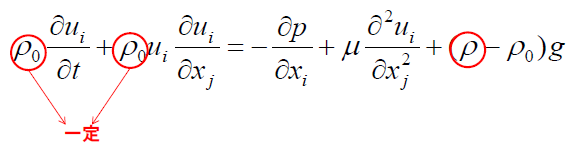
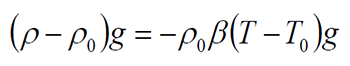
ブシネスク近似を用いることで、流体密度を温度の関数として解析を行うよりも収束が早くなる場合が多いですが、温度差には注意が必要です。圧縮性流体を用いて浮力を厳密に求める場合には温度差に制限はありません。しかしブシネスク近似を用いる場合は、温度差が大きい場合には近似による誤差が大きくなりますので、例えば流体として水を用いる場合は温度差が2[K]、空気の場合は15[K]以内が望ましいとされています。
D:境界条件による誤差
解析を行う場合には、実空間すべてを再現することはできませんので、解析空間として有限の領域を設定し、解析空間とその外の空間を区切る面に境界条件を与える必要があります。
使用する流体解析ソフトによっても分類が変わりますが、代表的な境界条件としては、以下の5つがあります。
- 流入条件:解析空間への流体の流入を許可する
- 流出条件:解析空間への流体の流出を許可する
- 開放条件:解析空間への流体の流入/流出ともに許可する
- 壁面条件:解析空間への流体の流入/流出ともに許可しない
- 対称条件:対称モデルの対称面として設定する
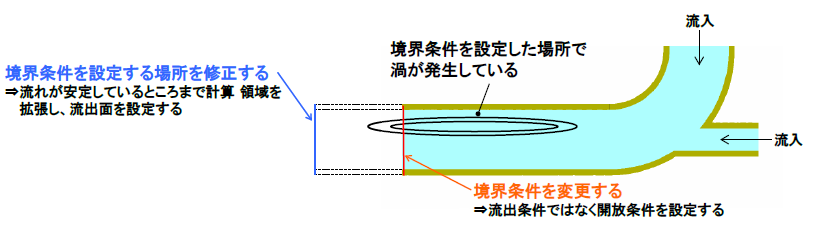
境界条件を設定する際には設定する場所と条件の両方に注意する必要があります。境界条件を設定する場所は解析領域のサイズによって変化しますが、 第2回のモデル形状による誤差_B:解析領域サイズによる誤差 でもご紹介したように、【必要十分な解析空間の確保】が重要です。図2のように、流れが均一でない場所に境界条件を設定すると全体の流れ場が変わってしまう可能性があります。このような場合には、ある程度流れが安定した場所に境界条件が来るように解析領域を拡大します。また逆流が発生すると予想される場所に境界条件を設定する場合には、流出条件ではなく開放条件を設定することが必要です。
境界条件の設定は再現したい現象にあわせる必要がありますが、その組合せによっては収束性が悪くなることもあり、注意が必要です。
例えば流入条件と流出条件に同一の物理量を指定してしまうと、保存則を満たせなくなるため計算の収束性が悪くなり、最終的に計算が発散する場合もあります。
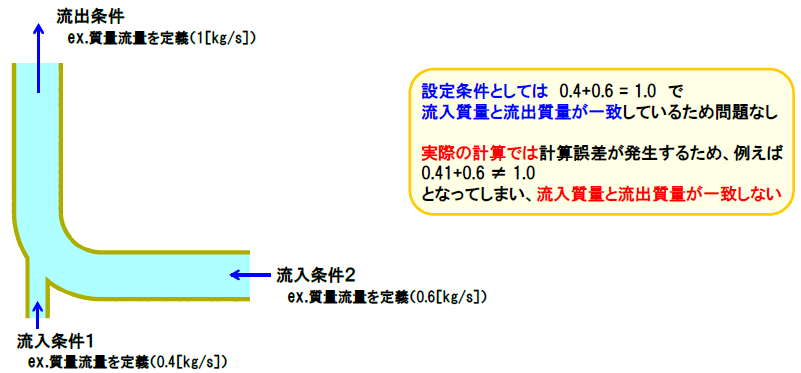
また図3のように、流入条件と流出条件を質量流量で指定した場合、実際の解析では必ず計算誤差が発生してしまうので、流入質量と流出質量が一致しなくなり、収束性が悪化する可能性が考えられます。このような場合にはどちらか一方の条件を圧力指定にするなど、流入・流出の条件を別の物理量で指定すると収束性の改善が見込めます。
このように境界条件を設定する際には【設定する場所と条件】に注意して設定を行うことが重要です。
E:初期条件による誤差
解析を行う際に初期条件を設定する場合があります。
特に非定常解析では初期条件の設定が必須となりますが、設定した初期条件によって解析結果が変化するため、どのような初期条件を設定するかが重要となります。
たとえば物理量の変化がまったくない状態(流れが発生していない状態)を初期状態として計算を開始すると、解析開始直後に物理量の変化が大きくなって計算が発散する場合もあります。そのような場合は解析初期の刻み時間を小さくすることや、事前に定常解析を行って初期状態を作成しておくことなどが必要となってきます。
定常解析では初期条件の設定は必須ではありませんが、適切な初期値を設定することで解析の安定性向上や、解析時間の短縮が見込める可能性があります。たとえば定常状態(最終的な状態)に近い状態を初期条件にすると、解析時間を短縮できる場合があります。定常解析では解が収束してしまえば初期条件の影響はありませんが、収束判定値が比較的緩やかな場合は初期条件の影響を受けて結果が変わってしまう可能性がありますので注意して下さい。
[ケーススタディ]乱流モデルの違いによる誤差
ここからはモデル化による誤差のうちA:乱流モデルの選択による誤差、について具体例を見ていきたいと思います。
目的
今回は乱流モデルの違いによる流れ場の違いを確認することを目的とし、乱流モデルを変更した場合の流れ場への影響や計算時間を確認します。
モデル
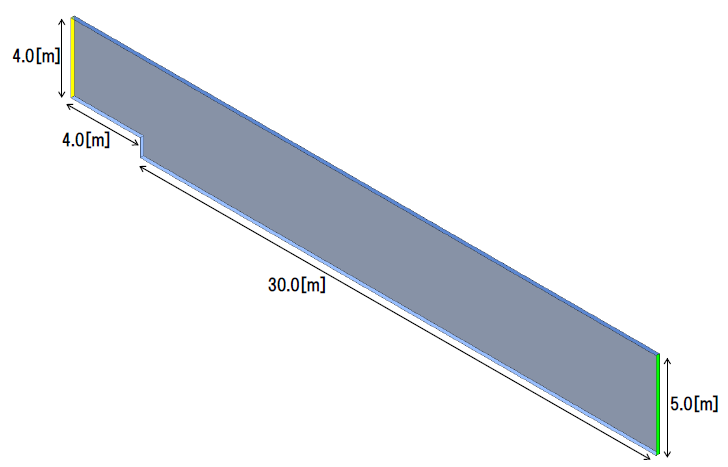
使用モデルを図4に示します。モデルは、全長34[m]、入口からキャビティまでの長さ4[m]、入口高さ4[m]、出口高さ5[m]、キャビティ高さ1[m]の、キャビティ(くぼみ)のある流路です
メッシュ
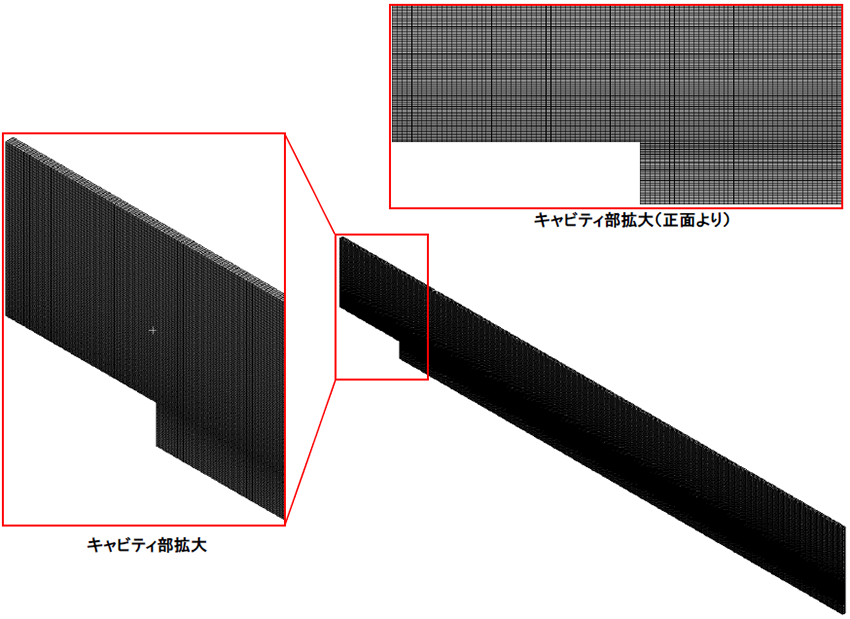
図5はモデルのメッシュを示します。今回は各モデルで同じメッシュを使用します。六面体メッシュで、流れに乱れが発生しやすいと考えられるキャビティ高さ周辺のメッシュを細かくしています。
表1にメッシュ数およびメッシュ品質を示します。六面体メッシュで作成しているため、メッシュの直交品質は0.71と高い品質になっています。

解析条件
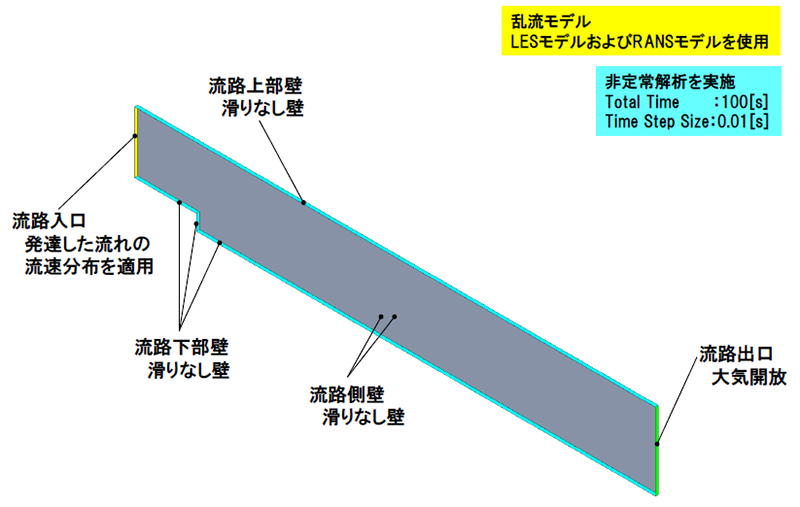
図6は解析条件を表します。乱流モデルとしてLESおよびRANSを用いた非定常解析を行います。解析時間は100[s]です。
境界条件、初期条件はともに同一の条件で、流路入口には十分に発達した流れの流速分布を適用しています。流路出口は大気開放(圧力1atmを想定)、流路壁は滑りなし壁と設定しています。
解析結果
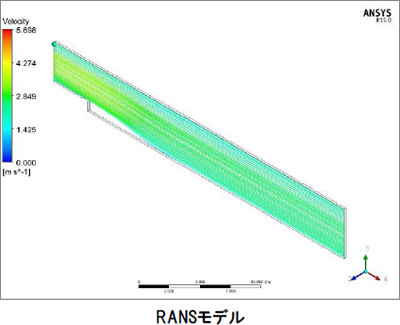
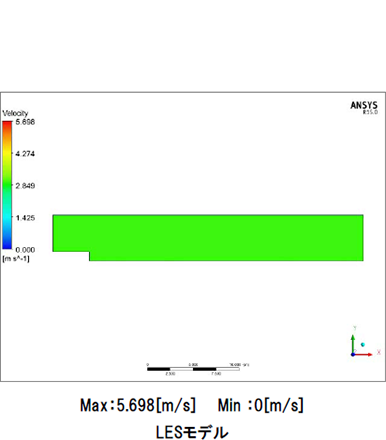
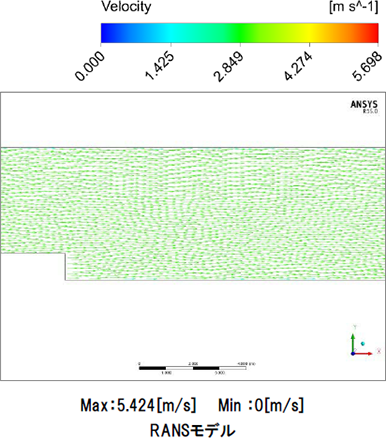
図7は各モデルの100秒後の流れを表す動画です。LESモデル、RANSモデルともにキャビティ下部では流速が遅くなっていることが確認できます。しかしLESモデルでは段差部から後流で流路全体にかけて流れに乱れが発生していることが確認できますが、RANSモデルでは流路全体の乱れは確認できません。
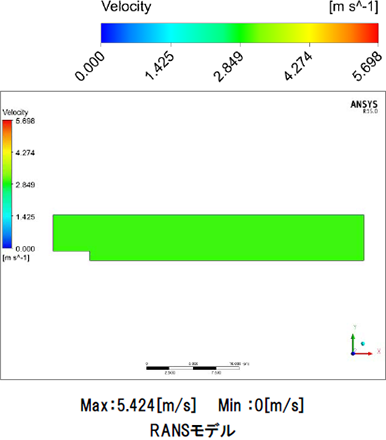
図8はzx平面における0秒から100秒までの流速分布を表す動画です。LESモデル、RANSモデルともに段差部直下で流速が遅くなり、キャビティ中央部の流速は速く、下部は遅い傾向がみられます。LESモデルでは時間的な平均化は行わず、メッシュより大きな渦は直接計算を行っているので、段差部で発生したより小さな乱れまで再現することができ、また発生した乱れが時々刻々と変化していることも確認できます。RANSモデルでは時間的にも、空間的にも平均化を行ってしまうので、段差部で発生した乱れは大きな流れとしてしか確認することができません。
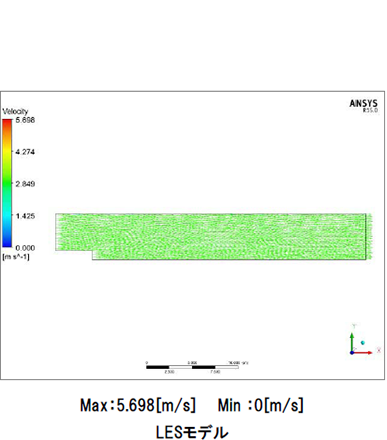
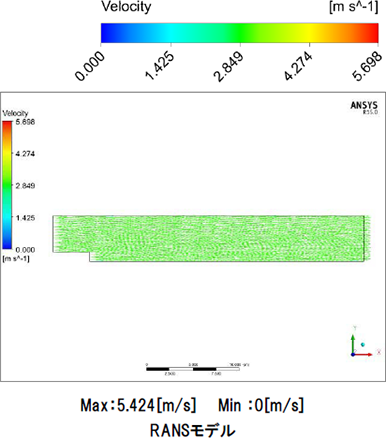
図9はzx平面における0秒から100秒までの流速ベクトルを表す動画です。LESモデル、RANSモデルともに段差部直下で渦が発生しています。LESモデルでは発生した渦による影響で時々刻々と流れ場が変化しています。RANSモデルでは渦が発達してしまった後は流れ場に大きな変化はありません。
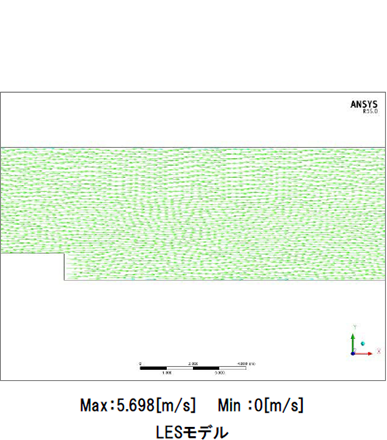
図10は図9と同じくzx平面における0秒から100秒までの流速ベクトルを表す動画で、段差部を拡大しています。LESモデルでは段差部で小さな渦が次々と発生していることが確認できます。RANSモデルでは段差部の渦が平均化されて大きな一つの渦となっています。
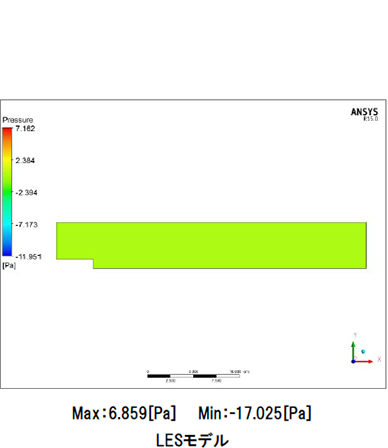
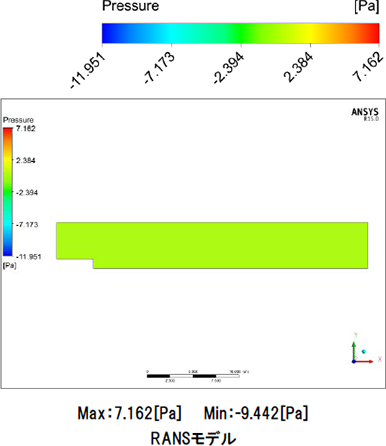
図11はzx平面における0秒から100秒までの圧力分布を表す動画です。LESモデル、RANSモデルともに段差部で発生した渦の影響で、段差上部の圧力が低くなっています。LESモデルでは小さな渦の発生に伴って圧力分布も時々刻々と変化しています。RANSモデルは渦が発達してしまった後は圧力分布に大きな変化はありません。最大圧力はLESモデルで6.859[Pa]、RANSモデルで7.162[Pa]、最小圧力はLESモデルで-17.025[Pa]、RANSモデルで-9.442[Pa]となりました。
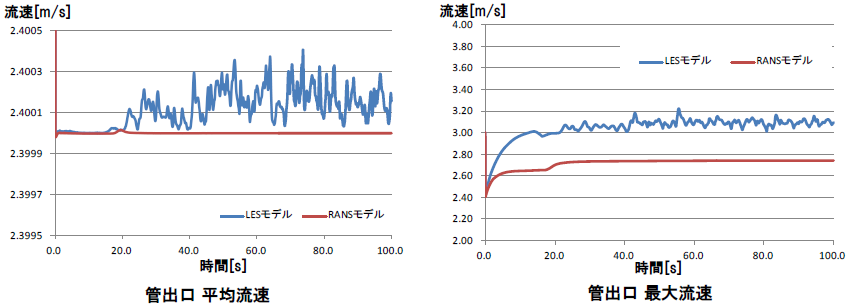
図12は管出口面における平均流速および最大流速の時間変化を表すグラフです。LESモデルは平均流速、最大流速ともに時間的な変動がみられ、RANSモデルは流速が安定する20[s]以降は大きな変動はみられません。また平均流速はどちらのモデルも2.4[m/s]程度でほとんど違いはみられませんが、最大流速はLESモデルでは3.2[m/s]、RANSモデルでは2.7[m/s]と違いがあります。これらの違いはLESモデルでは段差部で発生した乱れが平均化されずに管出口面まで到達しているためで、最大流速が大きくなり、時間的な変動も発生します。
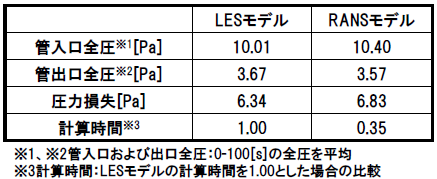
表2に各モデルの管入口、出口の全圧とそこから求められる圧力損失、および計算時間を示します。管入口、出口の全圧は0秒から100秒までの全圧の平均値です。圧力損失はLESモデルで6.34[Pa]、RANSモデルともに6.83[Pa]となりました。
計算時間は、RANSモデルの計算時間がLESモデルの約1/3となりました。
まとめ
今回は乱流モデルの違いによる流れ場の違いを確認することを目的とし、乱流モデルを変更して解析を行いました。その結果、以下のことが確認できました。
- 乱流モデルの違いによって流れ場に大きな違いがみられた。特に段差部での小さな渦の発生や、流れ場全体の時間変動についてはRANSモデルでは確認できず、LESモデルを用いた解析が必要であった。
- 圧力分布についても大まかな傾向はRANSモデルでも確認できたが、流れ場の影響を受けた時間変動はLESモデルでないと確認できなかった。また管入口、出口の平均流速や全圧、圧力損失には大きな違いはみられなかったが、最大流速、最大・最小圧力は乱流モデルの違いによる差異がみられた。
- 計算時間はRANSモデルのほうが大幅に短くなった。
乱流モデルの変更によるメリットとデメリット
今回の目的は乱流モデルの違いによる解析結果の違いを確認することでした。表3にLESモデルとRANSモデルを用いた非定常解析について、メリットとデメリットを示します。
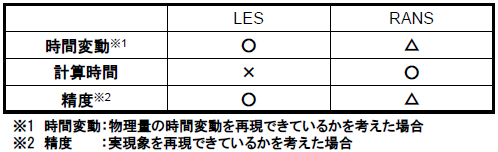
LESモデルを使用することで流れ場の時間変動を捉えることができますし、小さな渦まで再現できるため、実際の流れ場に近い状態を再現することが可能になります。しかし計算時間はRANSモデルの約3倍と、非常に長くなってしまう点に注意が必要です。また今回はLESモデル、RANSモデルとも同じメッシュを用いましたが、一般的にはLESモデルの方が細かいメッシュが必要となるため、解析コストの差はさらに大きくなることも考えられます。
そのため「流れ場の時間変動や小さな渦による変化が重要な場合はLESモデルを使用する」、「大まかな流れ場についてすばやく知りたい場合はRANSモデルを使用する」など、【再現したい流れ場】をきちんと把握し、【解析コストとのバランス】をみながら乱流モデルを決定して下さい!
おわりに
いかがでしたか?モデル化が原因となる誤差にも、いくつか種類があることがお分かりいただけたかと思います。目的に応じて上手にモデル化を行ってください。
第5回は、計算誤差について解説します。どうぞご期待ください。