CAEを学ぶ
ゴムの実挙動とそのモデル化［III］
山梨大学 工学部 土木環境工学科
吉田純司
パラメータの同定方法
これまでゴムの構成モデルとして、超弾性体、超弾性ダメージモデル、粘弾性モデルなどを紹介してきた。これらは代表的なゴムのモデルであるが、これ以外にも研究レベルでは、弾塑性体や粘塑性体を応用するモデルなどが提案されている。モデルが複雑になれば、基本的にはより細かな挙動を精度よく再現できるようになるものの、その一方でパラメータ数が増大しそれらを同定することが困難になるという問題が現れる。この問題は、実務においてゴム製品のFEM解析を実施する場合に大きな弊害の一つとなっており、実際にパラメータが3個あるいは4個以上のモデルを用いようとすると、どのようにそれらの値を決めたらよいか困った経験がある方も多いと思う。また、パラメータ数が多い複雑なモデルを用いるということは、その分、それらを同定するために色々な材料試験（振幅を変えて往路・復路を記録する引張り試験、多軸引張り試験、載荷速度を変化させる試験など）を実施する必要があるということであり、それらのデータを収集する手間も大きな課題となっている。
以下では、このようなパラメータ同定に関する問題について著者が用いている手法などについて紹介する。
評価関数の設定
単一の材料試験での評価関数
評価関数とは何かを説明するために、まずよくある簡単な例を考えてみる。変位を与え荷重を計測するタイプのゴムの単軸引張り試験（Uni-axial tension test）を実施し、伸張比 λ 1 と公称応力
P がデジタルデータとして得られている場合を想定し、i 番目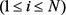 
の公称応力を P(i)のように記すことにする。このとき、モデルによる計算から得られる公称応力を 
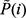とする。無論、
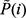を実際計算するためには、材料定数が既知である必要があるが「実験結果であるP(i)をよく再現できる材料定数」とは、数式ではどのように表されるだろうか。理想的には、各 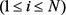においてP(i)と 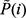が完全に一致することであり、数式で表すと例えば、
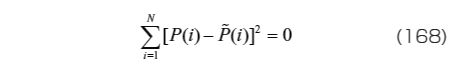
を満たす材料定数を探すこととなる。しかし、現実にはそこまで再現できる理想的なモデルは存在しない。実際には既往の材料モデルを用い、上式のような理想に近くなる材料定数として、
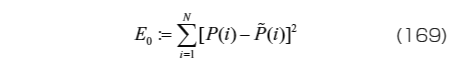
をなるべく小さくするものを探す方法が広く用いられている。上記の E 0 のように、材料定数の探索において評価に用いる関数のことを評価関数という。評価関数を小さくする材料定数の具体的な探索方法については後述する。
複数の材料試験での評価関数
前述した評価関数は単一の材料試験を対象としたものであるが、一般には複数の材料試験を対象にする場合の方が多い。例えば、変位を与え荷重を計測するタイプのゴムの単軸引張り試験と、均等二軸引張り試験（Equi-biaxial tension
test）を実施する場合を想定する。単軸引張り試験における i 番目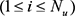 
の公称応力を P u (i) 、均等二軸引張り試験における i 番目 
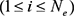の公称応力を P e
(i) とする。2つの実験で得られている P u (i) および P e (i) と、モデルによる計算結果 
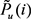および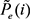 
とのそれぞれの差がなるべく小さくなるように材料定数を同定したい。
これに対応する評価関数としては、
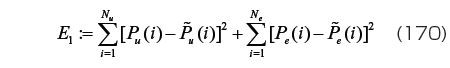
のようなものが考えられる。ただし、上式をそのまま用いると問題がある場合が多い。例えば、単軸引張り試験のデータ数 N u が極端に多く N u = 10000 であり、一方、均等二軸引張り試験のデータ数 N e が比較的少なく N e = 500 の場合を想定する。このとき、式（170）を用いると、E 1 を小さくするためには主に右辺第一項を優先的に小さくすれば良い事になってしまう（単軸引張り試験の方の差を優先的に小さくするような結果が得られる）。そこで両試験での結果を対等に扱うという意味で、データ数でそれぞれの差の二乗和を基準化する評価関数：
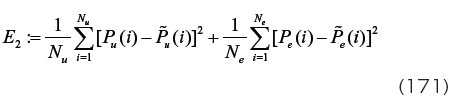
を用いるとよい。また、更なる改善方法として、
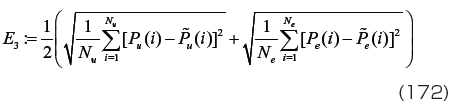
のような評価関数を用いると、E 3 の値はデータ一個当りの実験結果と計算結果の平均的な差を表すことになるため、E 3 の値から材料定数の良し悪しをある程度把握しやすくなる。
評価関数の更なる工夫
上述した式（172）の評価関数を用いると、ほとんどの場合で問題ないと思われるが、中には材料定数をうまく同定できない場合がある。例えば、 複数の材料試験での評価関数 と同様に単軸引張り試験と均等二軸引張り試験を実施し、単軸引張り試験では実験時に大きな変位を与えることができたため、公称応力が大きな値（例えば最大値が25[N/mm 2 ]）となり、一方、均等二軸引張り試験では実験時に比較的小さな変位しか与えられず公称応力が小さな値（例えば最大値が1[N/mm 2 ]）となる場合を想定する。式（172）では、両試験を対等に扱っているため、実験結果と計算結果の差も同等に扱うこととなる。例えば、各試験での実験結果と計算結果との平均的な差が0.1[N/mm 2 ]の場合には、単軸引張り試験にとってはこの差は微小であると言えるが、均等二軸引張り試験では比較的大きい値である。このような問題を回避するために、実験結果と計算結果の差に対する扱いを両試験で平等にする。具体的には、式（172）の評価関数において、それぞれの実験での公称応力の最大値で、差の平均値を基準化した評価関数：
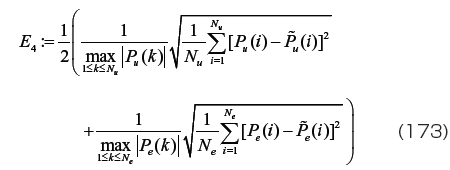
を用いるとよい。著者の経験では、ほとんどの材料定数の同定問題において、評価関数に式（173）を用いていれば問題ないと思われる。
以上のように、用いる材料試験の内容によって評価関数を工夫することで材料定数の同定で発生する問題を解決できる場合があることを覚えておいてほしい。
