CAEを学ぶ
ゴムの実挙動とそのモデル化[II]
山梨大学 工学部 土木環境工学科
吉田純司
ゴムを対象とした超弾性体
超弾性体の定義
超弾性体とは、厳密には応力とひずみ(伸張比)が一対一に対応する弾性体のうち、ひずみエネルギ密度関数(変形前の単位体積当りのひずみエネルギでスカラ量)が存在する材料モデルを指す。ひずみエネルギ密度とは、簡単に言えば応力が成した単位体積当りの仕事であり、応力をひずみで積分したスカラ量である。このことから、ひずみエネルギ密度関数をひずみで偏微分することで対応する応力を得ることができる。超弾性体のひずみエネルギ密度関数を
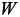 とすると、
とすると、 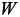 は剛体回転に対して不変でなくてはならないことから、式(7)の
は剛体回転に対して不変でなくてはならないことから、式(7)の 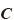 の関数として
の関数として 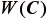 のように記述する。
のように記述する。
超弾性体には、等方性(変形の方向によらず同一の力学特性を示す)のモデルと、異方性(変形の方向により異なる力学特性を示す)のモデルが存在するが、ゴムは等方性として扱われることが多い。超弾性体に等方性を仮定すると、ひずみエネルギ密度関数
 が座標軸に依存しない条件より、
が座標軸に依存しない条件より、 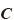 の不変量
の不変量 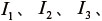 あるいは主値(固有値)
あるいは主値(固有値) 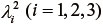 を用いて表すことができる。ただし、不変量とは、固有値を求める際の特性方程式の3つの係数を指し、具体的には、
を用いて表すことができる。ただし、不変量とは、固有値を求める際の特性方程式の3つの係数を指し、具体的には、
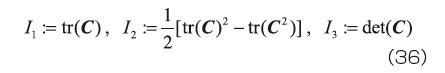
である。ただしtr(・)は(・)のトレース(対角項の和)を表す。不変量と固有値はともに方向(座標系)に依存しないことが知られている。
体積変形と等容変形の分離
体積変形の記述
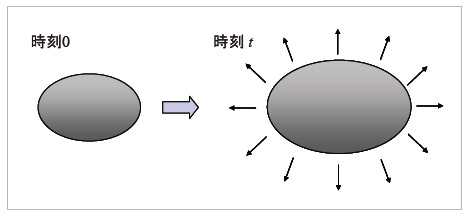
図-8 圧力などの外力を受け均一に膨張あるいは収縮する体積変形の概念図
体積変形とは、例えば図-8に示すように圧力などが作用し、物体が形状を変えずにどの方向にも均一に膨張あるいは収縮する変形を指す。体積変形では、任意の物質点 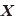 近傍にある微小線分が方向を変えずに定数倍される。このことより、変形前後での微小線分の倍率を
近傍にある微小線分が方向を変えずに定数倍される。このことより、変形前後での微小線分の倍率を 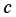 とすると、変形勾配テンソルは、
とすると、変形勾配テンソルは、
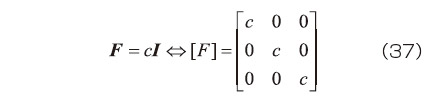
と表される。また、式(10)で示した体積変化率は、 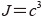 となる。
となる。
等容変形の分離
等容変形とは、任意の変形から体積変形を除外した残りを指し、せん断変形などがその代表例である。微小ひずみ問題では、両者はひずみレベルで足し算の形で分離できる。一方、大ひずみ問題では以下のように変形勾配テンソルを掛け算の形で分離できることが知られている。変形全体を記述する基本量は
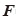 であり、式(37)に習うと、このうちの体積変形分は
であり、式(37)に習うと、このうちの体積変形分は 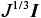 と表すことができる。このことから等容変形を表す部分を
と表すことができる。このことから等容変形を表す部分を 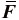 とすると、
とすると、 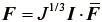 のような乗算分解の関係より、
のような乗算分解の関係より、
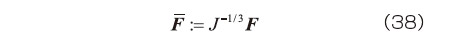
のように定義する。 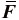 は単に
は単に 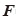 にスカラ
にスカラ 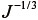 を掛けているだけの量であるが、
を掛けているだけの量であるが、 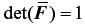 を常に満足していることから、体積変形の影響を受けないことになる。すなわち、係数
を常に満足していることから、体積変形の影響を受けないことになる。すなわち、係数 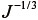 は
は 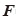 から体積変形分を除去するための補正係数の役割を果たしている。
から体積変形分を除去するための補正係数の役割を果たしている。
さらに式(7)に習い、 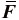 を用いて相対的な等容変形を表すテンソル
を用いて相対的な等容変形を表すテンソル 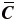 を
を
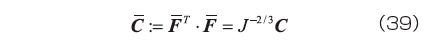
のように定義する。 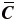 は右Cauchy-Greenテンソル
は右Cauchy-Greenテンソル 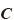 の等容変形分を表すことになる。このことから、構成モデルでは、
の等容変形分を表すことになる。このことから、構成モデルでは、 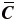 を等容変形を記述する代表量に、
を等容変形を記述する代表量に、 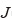 あるいは
あるいは 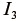 を体積変形を記述する代表量にとり定式化を行うことが多い。
を体積変形を記述する代表量にとり定式化を行うことが多い。
分離型の超弾性体
一般に、ゴムは微圧縮性あるいは非圧縮性としてモデル化することがほとんどであり、数値計算では体積変形と静水圧の関係に対し特別な処理が必要になる。このことから、構成モデルでは体積変形と等容変形を分離して扱う方法が主流となっている。
微圧縮性の超弾性体に対するひずみエネルギ密度関数 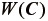 は、等容変形に対する寄与分
は、等容変形に対する寄与分 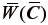 と体積変形による寄与分
と体積変形による寄与分 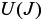 の和として次式のように記述できる。
の和として次式のように記述できる。
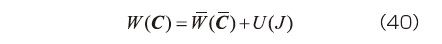
また、非圧縮性の超弾性体では、体積変形がないことから 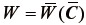 である。
である。
さらに等方性を仮定する場合には、等容変形に対するひずみエネルギ密度関数 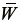 を
を 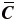 の1次および2次の不変量
の1次および2次の不変量 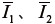 の関数として、
の関数として、
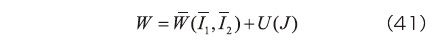
のように記述する、あるいは 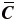 の主値( 固有値)
の主値( 固有値) 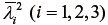 の関数として
の関数として
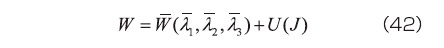
のように記述することができる。ここに
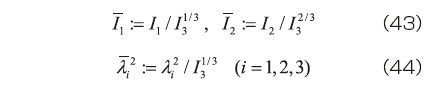
である。
ゴムによく用いられる超弾性体
ゴムを対象とした等方性の超弾性として、以下では代表的な 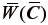 および
および 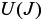 を紹介する。
を紹介する。
Mooney-Rivlinモデル
Mooney-Rivlinモデルは、  の不変量を用いるタイプで次式のように表される。
の不変量を用いるタイプで次式のように表される。
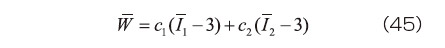
ただし  は非負の実定数であり、
は非負の実定数であり、 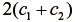 が微小変形でのせん断弾性係数に相当することが知られている。
が微小変形でのせん断弾性係数に相当することが知られている。
Mooney-Rivlinモデルは、材料定数が2個のみのため、それほど複雑な弾性挙動を再現することはできない。適用範囲の目安は、ひずみが10%程度以下である。
Ogdenモデル
Ogdenモデルは、 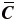 の主値(固有値)を用いるタイプで、次式のように表される 2)、4) 。
の主値(固有値)を用いるタイプで、次式のように表される 2)、4) 。
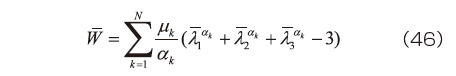
ただし 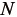 は正の整数で通常は
は正の整数で通常は 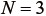 である。また、
である。また、 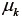 および
および 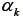 は、
は、 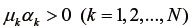 を満足する実定数であり、
を満足する実定数であり、 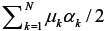 が微小変形でのせん断弾性係数に相当することが知られている(証明略)。
が微小変形でのせん断弾性係数に相当することが知られている(証明略)。
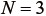 のとき、Ogdenモデルの材料定数は9個であり、数百%に至る大ひずみ領域までのゴムの弾性挙動を精度よく再現できることが知られている。ただし、あくまでも再現できるのは弾性挙動のみであり、本文2章で紹介した履歴ループやMullins効果を表すことはできない。
のとき、Ogdenモデルの材料定数は9個であり、数百%に至る大ひずみ領域までのゴムの弾性挙動を精度よく再現できることが知られている。ただし、あくまでも再現できるのは弾性挙動のみであり、本文2章で紹介した履歴ループやMullins効果を表すことはできない。
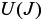 の具体例
の具体例
ゴムの体積変形を表すひずみエネルギ密度関数 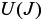 については、体積弾性係数を
については、体積弾性係数を 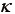 として、例えば次式の形がよく利用されている。
として、例えば次式の形がよく利用されている。
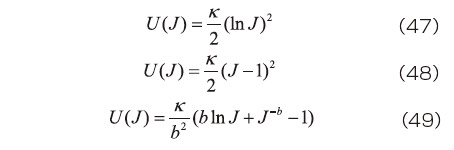
ただし、 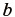 は正の実定数である。なお、解析対象のゴムが主として膨張変形のみ、あるいは収縮変形のみの場合であれば、式(47)or(48)で十分である。膨張と収縮がともに起こる場合には、式(49)を用いると、比較的実挙動と良く一致することが知られている
2) 。
は正の実定数である。なお、解析対象のゴムが主として膨張変形のみ、あるいは収縮変形のみの場合であれば、式(47)or(48)で十分である。膨張と収縮がともに起こる場合には、式(49)を用いると、比較的実挙動と良く一致することが知られている
2) 。
超弾性体に関する注意事項
材料に非圧縮を仮定すると 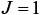 となることより、式(45)や(46)に含まれる
となることより、式(45)や(46)に含まれる 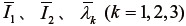 は、それぞれ
は、それぞれ 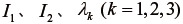 と同一になる。従って、「最初から後者を
と同一になる。従って、「最初から後者を 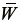 に用いても同じではないか?」という疑問が生じるかもしれない。しかし、実は応力を算出する際にその違いが現れる。後述するように応力の算出では
に用いても同じではないか?」という疑問が生じるかもしれない。しかし、実は応力を算出する際にその違いが現れる。後述するように応力の算出では 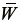 を
を 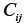 で偏微分する必要があるが、
で偏微分する必要があるが、 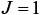 の条件を代入するのは 偏微分した後の式 になる。もし、偏微分する前に
の条件を代入するのは 偏微分した後の式 になる。もし、偏微分する前に
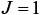 を用いると、すなわち
を用いると、すなわち 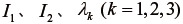 を
を 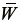 に最初から使うと、そこから得られる応力は、無変形状態にも関わらず非ゼロの応力が発生するという不具合を生じる。
に最初から使うと、そこから得られる応力は、無変形状態にも関わらず非ゼロの応力が発生するという不具合を生じる。
応力算出の一般論
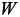 はひずみエネルギであることから、荒く言えば応力をひずみについて積分した値である。従って、
はひずみエネルギであることから、荒く言えば応力をひずみについて積分した値である。従って、 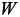 をひずみで微分すれば、応力を得ることができる。微圧縮性の超弾性体では、
をひずみで微分すれば、応力を得ることができる。微圧縮性の超弾性体では、 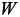 をGreen-Lagrangeひずみ
をGreen-Lagrangeひずみ 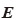 で偏微分すると、エネルギ共役である第2Piola-Kirchhoff応力テンソル
で偏微分すると、エネルギ共役である第2Piola-Kirchhoff応力テンソル 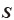 が算出されることが知られている 1)、2) 。具体的には、
が算出されることが知られている 1)、2) 。具体的には、
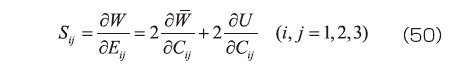
の関係が成立する。また、材料に非圧縮性を仮定する場合には、体積が変化しないという拘束条件から以下のように表される。
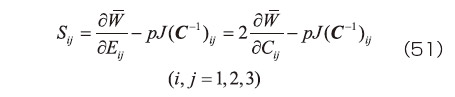
ただし 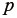 は不定静水圧と呼ばれ、変形からは決定できず、力(応力)の釣り合いから求められる。材料が非圧縮であるとは、体積を変化させようとする均等な直応力が材料に作用しても変形しない、ということである。逆に言えば、応力の一部が変形に依存しないということであり、それに相当するのがp
である。なお、非圧縮性を仮定すると式(51)の形になることについては、文献1)のpp.166-168に分かりやすい説明があるので参照されたい。
は不定静水圧と呼ばれ、変形からは決定できず、力(応力)の釣り合いから求められる。材料が非圧縮であるとは、体積を変化させようとする均等な直応力が材料に作用しても変形しない、ということである。逆に言えば、応力の一部が変形に依存しないということであり、それに相当するのがp
である。なお、非圧縮性を仮定すると式(51)の形になることについては、文献1)のpp.166-168に分かりやすい説明があるので参照されたい。
等方性の超弾性体のうち式(41)で表されるタイプのひずみエネルギ密度関数を用いると、式(50)あるいは式(51)右辺の各項は、偏微分の連鎖則より次式のように展開できる。
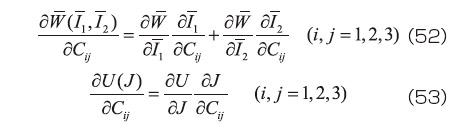
ただし、
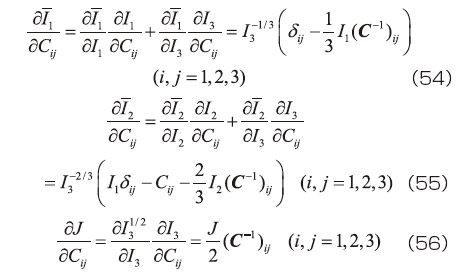
であり、これらの導出には、
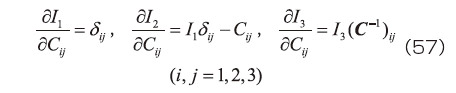
を用いている 1)、2) 。
一方、式(42)の 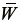 を用い、材料に微圧縮性を仮定する場合には、等方性であることから
を用い、材料に微圧縮性を仮定する場合には、等方性であることから 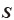 と
と 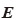 が共軸(主軸が同一)となる条件より、
が共軸(主軸が同一)となる条件より、
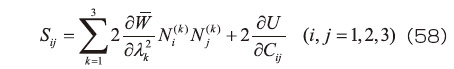
のように表される(証明略) 1) 。ただし、 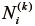 は、
は、 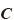 の
の 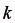 番目の主値
番目の主値 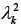 に対応する主軸
に対応する主軸 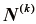 (単位の大きさの固有ベクトル)の第
(単位の大きさの固有ベクトル)の第 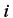 成分である。また、材料に非圧縮を仮定する場合には、式(51)に習い等容変形成分に静水圧分を加えて
成分である。また、材料に非圧縮を仮定する場合には、式(51)に習い等容変形成分に静水圧分を加えて
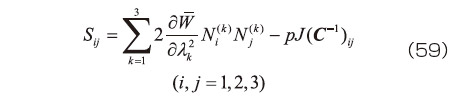
のように表される 2) 。なお、式(58)、(59)に含まれる 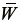 の偏導関数をさらに展開すると、
の偏導関数をさらに展開すると、
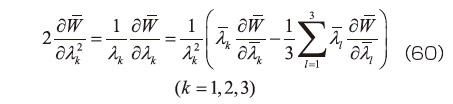
となる。
Mooney-Rivlinモデルを用いた計算例
図-1(前の記事の図)の二軸引張り変形を対象として、式(45)に示したMooney-Rivlinモデルの式展開を具体的に示す。ここでの事例を通して超弾性体の計算方法を学んでほしい。ただし、以後の計算はすべて非圧縮を仮定して行う(微圧縮性を仮定すると手計算ではできない)。
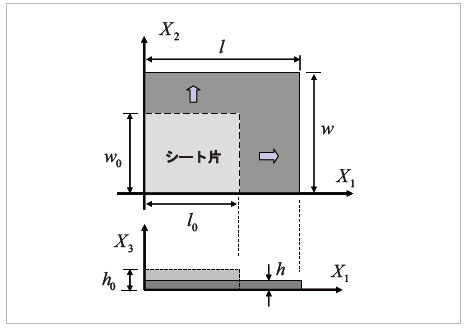
図-1 ゴムシートのニ軸引張り変形(前号からの抜粋)
図-1の引張り変形では、非圧縮性を仮定すると、その変形は式(16)~(19)のような形で表すことができる。従って  に関連した不変量については、
に関連した不変量については、
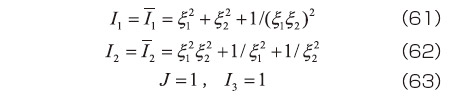
のように表される。
一方、応力の算出に必要なものは、
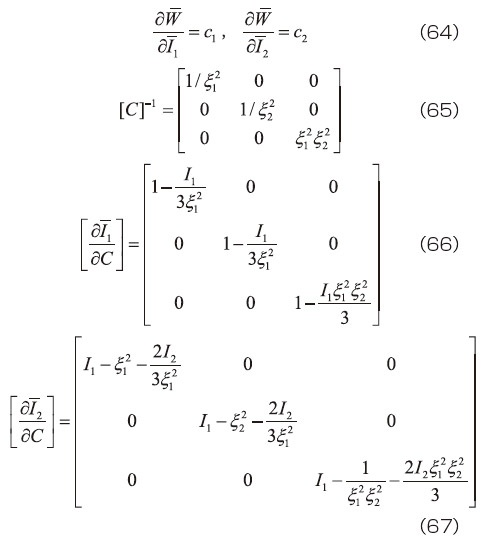
となることから、これらを式(51)に代入すると、第2Piola-Kirchhoff応力テンソル 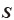 の行列表示は、
の行列表示は、
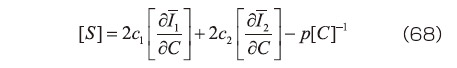
となる。さらに式(22)を参照して 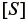 の3行3列成分がゼロになる条件から、不定静水圧
の3行3列成分がゼロになる条件から、不定静水圧 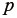 を求めると、
を求めると、
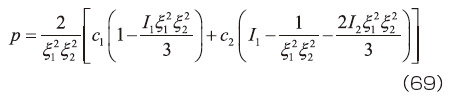
となる。この 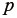 を式(68)に代入して、Mooney- Rivlinモデルでの第2Piola-Kirchhoff応力
を式(68)に代入して、Mooney- Rivlinモデルでの第2Piola-Kirchhoff応力 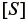 を得ることができる。また、式(14)、(15)の関係を用いると、公称応力
を得ることができる。また、式(14)、(15)の関係を用いると、公称応力 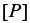 や真応力
や真応力 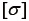 も容易に算出できる。通常は、モデルでの公称応力と、計測した荷重から得られる公称応力(式(21))の1行1列成分や2行2列成分を比較して、材料定数
も容易に算出できる。通常は、モデルでの公称応力と、計測した荷重から得られる公称応力(式(21))の1行1列成分や2行2列成分を比較して、材料定数  を決定する。
を決定する。
なお、式(69)において無変形状態では、 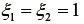 、
、 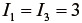 となることより
となることより 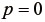 が成立するが、仮に式(45)において
が成立するが、仮に式(45)において 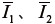 に代わり
に代わり 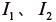 を採用したモデルを用いると、無変形状態でも
を採用したモデルを用いると、無変形状態でも 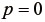 とならず、非ゼロの応力が存在するという不合理が生じる。
とならず、非ゼロの応力が存在するという不合理が生じる。
Ogdenモデルを用いた計算例
二軸引張り変形
Mooney-Rivlinモデルでの場合と同様にして、図-1のニ軸引張り変形を対象とし、非圧縮を仮定した場合( 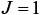 )における式(46)のOgdenモデルの展開を示す。まず、図-1の引張り変形では、
)における式(46)のOgdenモデルの展開を示す。まず、図-1の引張り変形では、
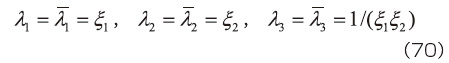
となる。また、式(18)より  は対角行列となることから、主軸方向は座標軸と一致する。すなわち、式(58)や(59)で用いた主軸
は対角行列となることから、主軸方向は座標軸と一致する。すなわち、式(58)や(59)で用いた主軸 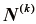 の行列表示は、
の行列表示は、
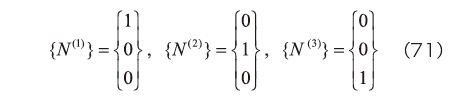
となる。このことより、式(59)を行列表示すると、
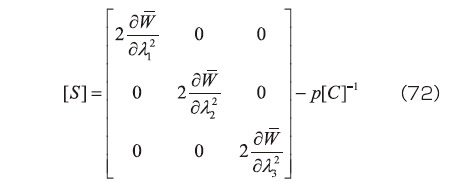
の関係を得る。ここで式(46)より
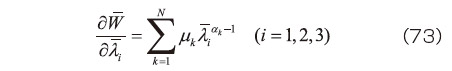
となり、この関係に式(70)を代入すると、
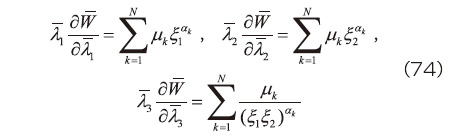
となるから、これらを式(60)に用いると、式(72)右辺の各成分を具体的に算出できる。
さらに、式(72)において 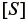 の3行3列成分がゼロになる条件より不定静水圧を求めると、
の3行3列成分がゼロになる条件より不定静水圧を求めると、
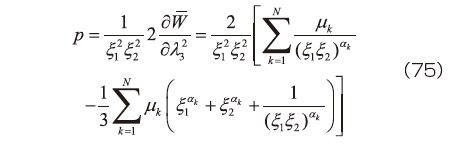
である。この 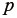 を式(72)に代入してOgdenモデルでの第2Piola-Kirchhoff応力
を式(72)に代入してOgdenモデルでの第2Piola-Kirchhoff応力 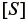 を得ることができる。また、式(14)、(15)の関係を用いると、公称応力
を得ることができる。また、式(14)、(15)の関係を用いると、公称応力 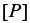 や真応力
や真応力 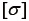 も容易に算出できる。通常はモデルから得られる公称応力と、計測した荷重から得られる公称応力の1行1列成分や2行2列成分を比較して、材料定数
も容易に算出できる。通常はモデルから得られる公称応力と、計測した荷重から得られる公称応力の1行1列成分や2行2列成分を比較して、材料定数 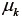 および
および 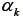 (
( 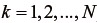 ) を決定する。
) を決定する。
なお、式(75)において無変形状態では、 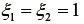 より、
より、 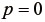 が成立する。仮に式(46)において
が成立する。仮に式(46)において 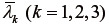 に代わり
に代わり 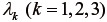 を採用したモデルを用いると、無変形状態においても
を採用したモデルを用いると、無変形状態においても 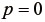 とならず、非ゼロの応力が存在するという不合理が生じる。
とならず、非ゼロの応力が存在するという不合理が生じる。
単純せん断変形
式(58)、(59)で示したOgdenモデルの応力を求める式では、式中に主軸が含まれていることから、単純せん断変形を例に取ると理解しやすい。単純せん断変形では、式(24)より 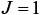 となるから、伸張比(主軸伸張比)は、式(30)より、
となるから、伸張比(主軸伸張比)は、式(30)より、
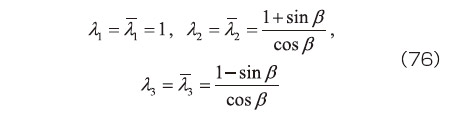
であり、 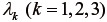 に対応する主軸の行列表示
に対応する主軸の行列表示 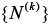 は式(31)に順に示したとおりである。
は式(31)に順に示したとおりである。
ここで、 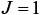 を用いて、式(59)の関係を行列表示で表すと、以下のようになる。
を用いて、式(59)の関係を行列表示で表すと、以下のようになる。
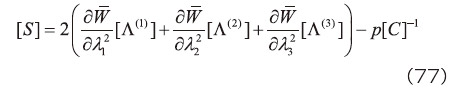
となる。ただし 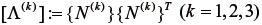 は、その
は、その 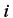 行
行 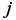 列成分が
列成分が 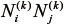 となる3行3列の行列である。また、上式に含まれる
となる3行3列の行列である。また、上式に含まれる 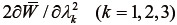 は、式(60)および式(73)の関係に式(76)を代入して算出する。なお、式(31)、式(76)より、主軸伸張比
は、式(60)および式(73)の関係に式(76)を代入して算出する。なお、式(31)、式(76)より、主軸伸張比 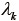 だけでなく主軸
だけでなく主軸 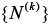 も変形に応じて変化するので、
も変形に応じて変化するので、 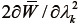 および
および 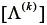 は変形ごとに算出することに注意を要する。
は変形ごとに算出することに注意を要する。
さらに,非圧縮性を仮定している場合には,せん断変形による体積変形がなく奥行き方向の応力が生じないことから,式(35)における 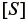 の3行3列成分が0となることより、不定静水圧
の3行3列成分が0となることより、不定静水圧 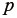 を決定できる。最後に得られた
を決定できる。最後に得られた 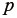 を式(77)に代入し、
を式(77)に代入し、 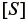 を得ることができる。
を得ることができる。
超弾性体のまとめ
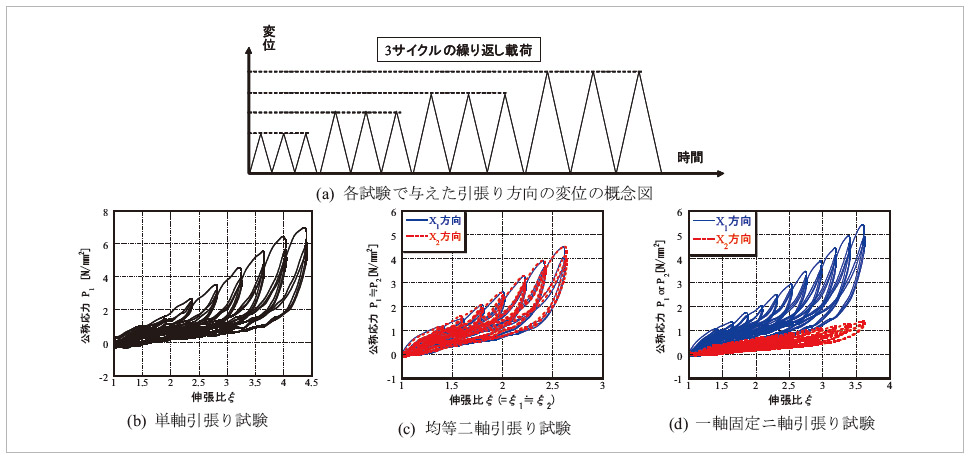
本節では、ゴムを対象とした超弾性体の基礎事項について説明した。超弾性体から得られる応力-伸張比の関係はあくまで弾性であるので、基本的に図-3(前の記事の図)に示すようなゴムの繰り返し挙動を再現することはできない。ゴムのMullins効果や履歴ループの大きさは、ゴムの加硫時に加える添加物に依存する。そのため、カーボンブラック等の添加物が少なくほぼ弾性体とみなせるゴムの場合には、超弾性体でも十分な精度でモデル化可能である。一方で添加物が多いゴムをモデル化する場合に、超弾性体の使いどころとしては、対象とるゴム製品が一回きりの載荷を受ける場合(往路のみ)のような単調な載荷である場合などに限られる。