CAEを学ぶ
ゴムの実挙動とそのモデル化[I]
山梨大学 工学部 土木環境工学科
吉田純司
はじめに
ゴム材料は、タイヤ、構造物の免震装置、電子機器の防振装置、防舷材などを始めとして数多くの工業製品に応用されている。
工業用途のゴム材料は、通常、生ゴム(生の天然ゴム)や合成ゴムを加硫して精製されるが、その際にカーボン、可塑剤、オイルなど様々な添加剤を加えることで、限界伸び、耐久性、耐候性、減衰性能などを調整して用いられる。この添加剤の影響により、ゴム材料は、大ひずみ下で複雑な力学特性を示す。また、非圧縮に近い性質(以後、微圧縮性と呼ぶ)を有しており、数値計算では特別な取り扱いをする必要がある。
近年、情報機器の発展により、材料・幾何学非線形を含む3次元の応力解析を手軽に実施可能なハード・ソフトが整いつつある。非線形の解析で有意な結果を得るためには、対象に用いられている材料の力学特性と、使用範囲をよく吟味し、適切な構成モデルとその材料定数を選定する必要がある。しかし、ゴム材料については、国内外でも公開されている材料試験データは希少であり、様々なひずみレベルでの多軸の繰り返し変形下での力学特性は必ずしも明らかにされていない。また、構成モデルの取り扱いには、非線形の連続体力学の学習が必須であり、構成モデルの利用という実用的な観点から、わかりやすく説明している文献は非常に少ない。
そこで本講座では、免震・防振装置に用いられているゴム 1) を例として取り上げ、その力学特性と代表的な力学モデルの基礎事項を解説する。
以下の本文では、説明のため一部にベクトルや二階のテンソルを用いるが、ボールド(太字)はテンソルやベクトルを指し、それらの直行デカルト座標での成分は、右下に添字をつけて表す。また、それらの成分を行列として表示する場合にはベクトルには中括弧、テンソルには大括弧をつけて表す。例えば、テンソル
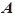 に対して、
に対して、 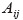 は
は 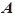 の
の  成分を指し、
成分を指し、  は
は 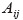 を
を 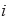 行
行 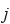 列成分にもつ3行3列の行列を表すものとする。また「:=」は定義を表すものとする。
列成分にもつ3行3列の行列を表すものとする。また「:=」は定義を表すものとする。
なお、本解説では、非線形連続体力学のうちゴムの力学を理解するための最低限の基礎知識のみを説明していくが、詳しく勉強したい方は、文献 2) 、3) 、4) 、5) などを参照されたい。
ゴムの力学特性
力学特性の記述方法
変形が簡易で一様である材料試験などでゴムの変形を記述するためには、伸張比と呼ばれる量が用いられる。伸張比とは、簡単に述べると、変形後の長さを変形前の長さで除した量である。
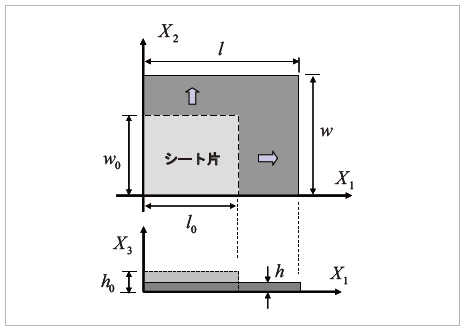
図-1 ゴムシートのニ軸引張り変形
具体例として、図-1に示すように、無変形状態(時刻0)で長さ 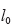 、幅
、幅 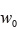 、厚さ
、厚さ 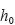 のゴムシートが二方向に引張り変形を受け、時刻
のゴムシートが二方向に引張り変形を受け、時刻  において長さ
において長さ 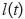 、幅
、幅 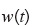 になる状態を考える。このとき、長さ方向(
になる状態を考える。このとき、長さ方向( 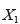 方向)、幅方向(
方向)、幅方向( 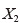 方向)の伸張比は、それぞれ以下のように記述できる。
方向)の伸張比は、それぞれ以下のように記述できる。
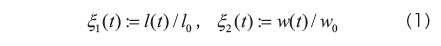
また、シートの厚み方向(  方向)については、初期状態より縮んでおり、時刻
方向)については、初期状態より縮んでおり、時刻  での厚みを
での厚みを 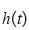 として、伸張比は、
として、伸張比は、
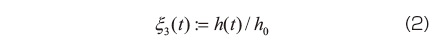
となる。ただし、通常、材料試験では、厚み方向の変形を各時刻で計測することが難しいため、hは未知である。そこで、ゴムが非圧縮に近い性質を有すること、すなわち変形を受けても体積がほとんど変化しない性質を利用すると、
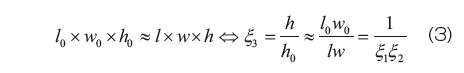
の関係を得る。すなわち 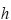 は、シートの初期の寸法と、
は、シートの初期の寸法と、  、
、 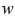 を計測していれば、近似的に得られることになる。このように、シートを用いたゴムの引張り試験などでは、一般に長さ
を計測していれば、近似的に得られることになる。このように、シートを用いたゴムの引張り試験などでは、一般に長さ  、幅
、幅 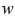 を計測し、変形の尺度として伸張比
を計測し、変形の尺度として伸張比 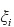 (
( 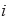 =1,2,3)を用いる。なお、非一様な変形で伸張比を定義する方法については後述する。
=1,2,3)を用いる。なお、非一様な変形で伸張比を定義する方法については後述する。
一方、応力については、シートを引張る荷重値と変形前の形状から算出できる公称応力(第1Piola-Kirchhoff応力とも呼ばれる)が力の尺度としてよく用いられる。具体的には、図-1において時刻  での長さ方向(
での長さ方向( 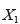 方向)の荷重値を
方向)の荷重値を
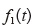 、幅方向(
、幅方向( 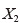 とすると、変形が一様でかつ内部に作用する力(内力という)は荷重値に等しいことから、各方向での公称応力は、荷重値を変形前の断面積で除して、
とすると、変形が一様でかつ内部に作用する力(内力という)は荷重値に等しいことから、各方向での公称応力は、荷重値を変形前の断面積で除して、
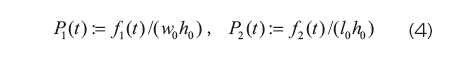
と記述できる。シートの厚み方向については、拘束がなく荷重値はゼロであるから、内力、応力ともにゼロである。
以上のように、シート型のゴムを用いた引張り試験では、計測した変位や荷重から(  )と(
)と(  )を算出し、材料の力学特性として伸張比と公称応力の関係を記述することが多い。
)を算出し、材料の力学特性として伸張比と公称応力の関係を記述することが多い。
実際のゴムの力学特性
ゴムの引張り試験
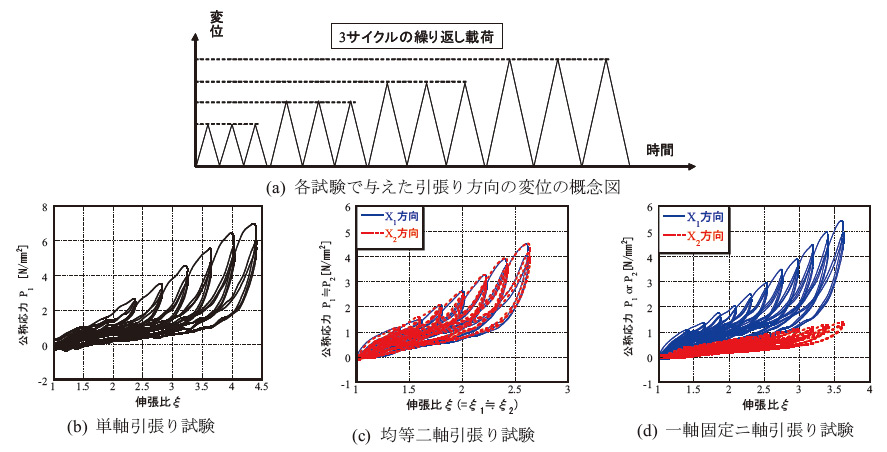
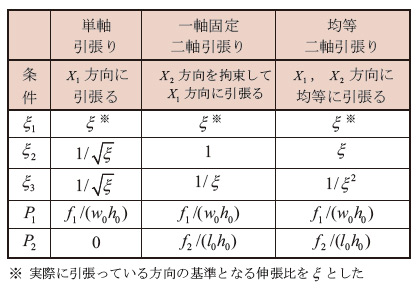
シートを用いたゴムの引張り試験では、単軸引張り試験、一軸固定ニ軸引張り試験、均等二軸引張り試験の3つの場合が広く実施されている。これらは、いずれも図-1で示した一般的なニ軸引張り状態の特殊なケースである。それぞれの引張り試験の概要図を図-2に、特徴を表-1に示す。

図-2 各引張り試験での変形の概念図
伸張比と公称応力の関係
ここでは、例として、防振部材に用いられる天然ゴム(カーボン等の添加剤あり)の各引張り試験での伸張比と公称応力の関係を示し、その力学的な特徴を説明する。対象とする天然ゴムは、表-2のような基本性質を有している。

図-3 (b) ~ (d) 1) は、上述した3つの引張り試験において、図-3
(a)のような3サイクルずつの繰り返しの漸増変位を引張り方向に与えた場合における伸張比と公称応力の関係を表している。また、図-3 (d)において伸張比レベル(振幅)が約3.3以上の  方向の履歴ループを図-4に示す。
方向の履歴ループを図-4に示す。
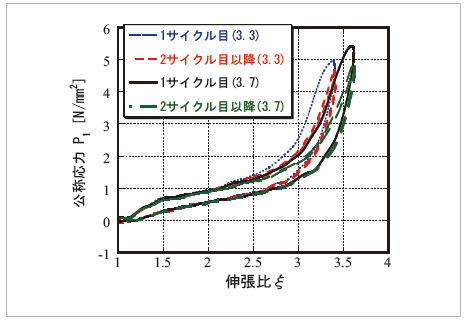
図-4 2つの伸張比レベルでの履歴ループ形状の比較
(凡例の括弧内の数値は,各サイクルでの伸張比の最大値を表す)
ゴムは近似的に弾性体としてモデル化されることが多い。しかし、図-3からわかるように、少なくともここで対象としたゴムの繰り返し載荷下での挙動は、弾性体とは大きく異なっている。
具体的には、まず第一に、載荷時と除荷時の曲線が異なっていることがわかる。一般にこの2つの曲線を合わせたものを履歴ループと呼び、その面積分のエネルギは熱として放出されることになる。この履歴ループは,伸張比レベル(振幅)によって異なる形状を示してる点に特徴があるといえる。第二に、同一の伸張比レベルでも、1サイクル目のみ大きな応力値をとる載荷曲線を描き、2サイクル目以降はおおむね同一の履歴ループを示している(図-4参照)。すなわち、初めて経験する伸張比のレベルでは大きな応力値をとる載荷曲線を示し、一度、変形を経験すると、ある程度安定した履歴ループの形状を示す。この過去に経験した変形に依存する性質は、Mullins効果 3)、6) と呼ばれる。