プログラマブルマテリアル-材料物性をデザインする

本解析事例は、マルチスケールシミュレーションにより「0.0～0.5以上のポアソン比」を持つハニカムライクなミクロ構造のプログラマブルマテリアルを設計したものです。
複数の異なる材料を混合したり、均質な素材に対して空隙を作ることによって、見かけの材料物性値を制御することができます。例えば、素材の内部に人工的に空隙を配置することで、ポアソン比や線膨張係数をゼロにするような材料も設計できることが知られています。
このような材料は【メタマテリアル】や【プログラマブルマテリアル】等と呼ばれ、産業的な応用を目的として古くから研究の対象とされてきました。
これまで、このような材料は目的の材料挙動となる構造が分かったとしても、その構造を持つ材料を製造することが困難であるケースが多くありましたが、近年の3Dプリンターに代表される革新的な製造技術の進歩によって実用化が期待されるようになっています。

今回の解析は、マルチスケールシミュレーションを用いてそうした新たな構造材料の物性予測をおこなうものであり、今後の新素材開発などに応用できる事例となります。

解析モデル

解析フロー

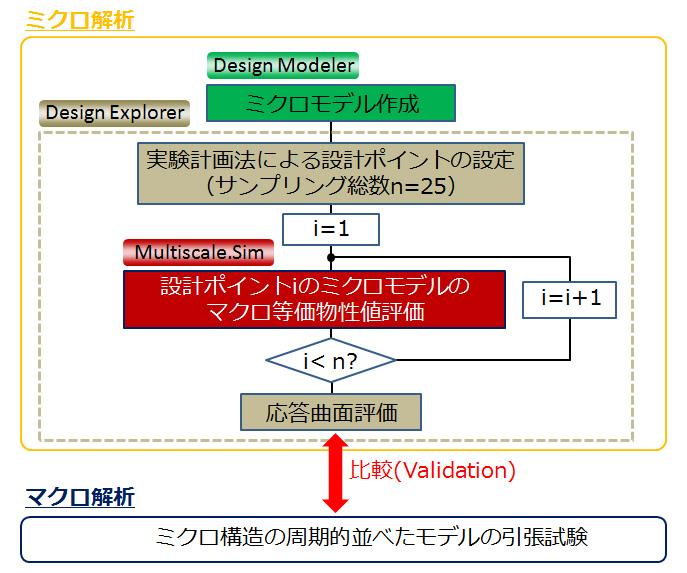
図１に今回の解析事例の全体的な手順を示しました。本解析では様々なミクロ形状における等価物性値を、応答曲面を用いて可視化することを目的とします。ミクロモデルはDesign Modelerを用いて作成しました。ここで、設計変数とする2つの形状パラメータの設定も同時に行いました。
続いて、応答曲面をプロットするためのサンプリング点(設計変数のセット)を実験計画法によって決定し、各点のミクロモデルにおける等価物性値をMultiscale.Simを用いて評価しました。離散的に評価された等価物性値は、近似関数によって応答曲面として可視化されます。実験計画法に基づく応答曲面の作成作業はDesign Explorerを用いて行いました。
最後に、応答曲面の結果の妥当性を確認するために、ミクロモデルを周期的に並べたマクロ解析モデルに対して引張試験の解析を行い、その結果を応答曲面と比較しました。

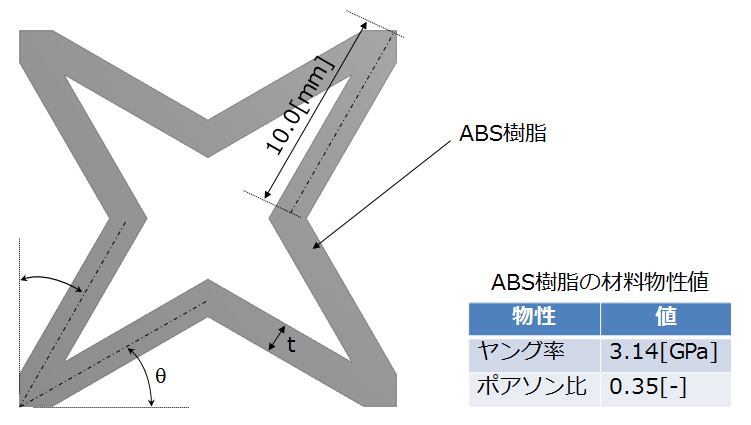
ミクロモデルの概要

図2にMultiscale.Simで等価物性値を取得するために使用したミクロモデル(ユニットセル)の外観を示します。Multiscale.Simが採用している均質化法では、このユニットセルが、全ての方向に周期的に並んでいることを想定して、仮想的な材料試験(以後、数値材料試験と呼ぶ)を実施します。ミクロモデルを構成する素材は、3Dプリンターに用いられることも多いABS樹脂を採用しました。形状パラメータとしては、骨格の角度と厚みtの2つを設定し、これらのパラメータの値に対する、みかけの材料物性値の関係を応答曲面として評価しました。