MEMSくし型フィンガー形状の静電場解析による最適化設計

“汎用有限要素法解析ツールAnsys”と、” 最適設計支援ツールOptimus ”を用い、静電場解析におけるMEMSくし型フィンガー形状の最適化を行いました。本事例では、単に最適解を算出するにとどまらず、設計の不確定要因（バラツキ）が応答に及ぼす影響（ロバスト・信頼性解析）を取り入れた最適化を行っています。今回モデル形状は、Ansysのモデリング機能を使用し作成しております。

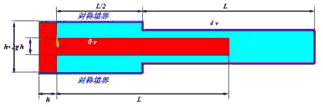
設計変数
・Length 95≦x≦105
・Gap 4.5≦x≦5.0

目的関数
・最大変位→ ターゲット値0.1

Process Automation

Optimusと接続可能なアプリケーションは、以下の条件を満たしている必要があります。

1. 入出力ファイルがText形式であること
2. バックグラウンドで実行可能なこと

Ansysは上記条件を満たしていますので、Optimusにて容易に自動化設定が可能です。

Optimusによる自動実行の流れ

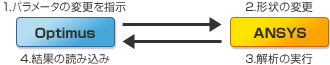
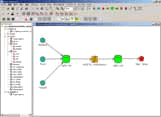
上図の自動実行の流れを、Optimusにて定義すると右図のようになります。Optimusでの自動設定は、ブロック線図によって直感的に定義する事が可能で、今回の事例であればわずか10分足らずで自動化設定が可能です。
一度Optimusで自動実行の仕組みを作れば、その後はOptimusのGUIを使って、何度でも解析を繰り返し実行する事ができます。よって、どなたにでも解析が実行できる環境が整います。
自動化設定をすることによって、これまで解析者の負担となっていた、パラメータ組み合わせの作成（直交表・実験計画法）や、数値入力、解析の実行、ポスト処理の実行といった非生産的作業を激減させる事ができ、設計業務の効率化を図る事ができます。

Optimusによる自動実行のメリット

• 非生産的業務からの解放（パラメータ入力等）
• 設計期間の短縮化
• 製品品質の向上
• CAD・CAEライセンスの有効活用（夜間・休日など）
• ケアレスミスの削減

Design Optimization / Robust & Reliability

始めのステップとして、決定論的最適解を求めます。まずは実験計画法・応答曲面法により、設計空間を分析します。この作業により、パラメータ同士の寄与度・相関性等の、設計において非常に重要な情報を得る事ができます。この考察から得られたポイントを元に、大域的最適化アルゴリズムである、焼きなまし法を実施します。これにより、決定論的最適解を得る事ができました。
次に、得られた決定論的最適解の設計変数に対し、下記の通りに分布（バラツキ）を与え、モンテカルロ法を実施し目的関数である最大変位のσ（シグマ）を計算します。

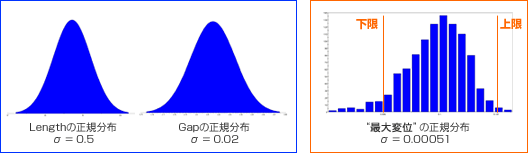
モンテカルロ法によって得られた最大変位のσは0.00051でした。さらに目的関数のσが上限値、下限値を超えてしまう”失敗の確率”を、FORM (First Order Reliability Method)によって求めます。FORMによって得られた失敗の確率は、上限=1.0%、下限=4.4%となりました。
上記結果を用い最終ステップとして、最大変位のσ（0.00051)及び、σが制約の上限・下限を超えてしまう失敗の確率を最小化する、ロバスト・信頼性最適化を行います。

Optimal Design

ロバスト・信頼性を考慮した最適解は以下の通りです。

	バラツキ考慮前の最適解 （決定論的最適解）
設計変数
Length	98.71464
Gap	4.81468
出力値
変位(Displacement)	0.1000006
σ	5.20E-04
下限値を超える確率	4.43%
上限値を超える確率	0.96%

バラツキ考慮後の最適解 （確率論的最適解）
100.5638
4.76845
0.100157
2.36E-06
0.00%
0.00%

目的関数である変位は、バラツキ考慮前も考慮後も、ほぼターゲットである0.1という解を算出できておりますが、最終目的であるσ・制約を超える確率に注目しますと、考慮前・考慮後で明らかに差が出ているのがわかります。特に制約を超える確率においては、上下限共に0.00%を実現しております。

Summary

Optimusによる解析（Ansys)の自動化

解析者にとって非生産的作業である、パラメータ入力などの繰返し解析作業をOptimusが自動化し、作業効率を劇的に改善する事ができました。

ロバスト・信頼性機能

設計不確定要因（設計変数のバラツキ）を考慮し、目的関数のσ（ロバスト）と、σが制約を超えてしまう確率（信頼性）を最小化する